Версия 11:44, 22 июня 2010

Гипермаркет знаний>>Математика>>Математика 8 класс>>Математика: Определение декартовых координат

                                        ОПРЕДЕЛЕНИЕ ДЕКАРТОВЫХ КООРДИНАТ

Проведем на плоскости через точку О две взаимно перпендикулярные прямые x и у — оси координат (рис. 170). Ось x (она обычно горизонтальная) называется осью абсцисс, а ось у — осью ординат. Точкой пересечения О — началом координат — каждая из осей разбивается на две полуоси. Условимся одну из них называть положительной, отмечая ее стрелкой, а другую — отрицательной.

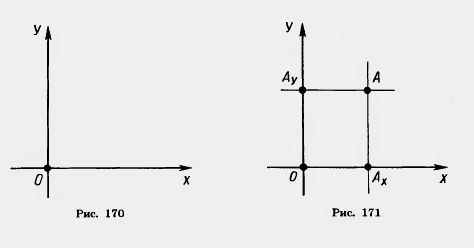
Каждой точке А плоскости мы сопоставим пару чисел — координаты точки — абсциссу (x) и ординату (у) по такому правилу.

Через точку А проведем прямую, параллельную оси ординат (рис. 171). Она пересечет ось абсцисс х в некоторой точке А_х. Абсциссой точки А мы будем называть число х, абсолютная величина которого равна расстоянию от точки О до точки Ах. Это число будет положительным, если Ах принадлежит положительной полуоси, и отрицательным, если А_х
 

 
принадлежит отрицательной полуоси. Если точка А лежит на оси ординат у, то полагаем х равным нулю.

Ордината (у) точки А определяется аналогично. Через точку А проведем прямую, параллельную оси абсцисс x (см. рис. 171). Она пересечет ось ординат у в некоторой точке A_y. Ординатой точки А мы будем называть число у, абсолютная величина которого равна расстоянию от точки О до точки A_y. Это число будет положительным,  если  А_у   принадлежит положительной полуоси,и отрицательным, если А_у принадлежит отрицательной полуоси. Если точка А лежит на оси абсцисс x, то полагаем у равным нулю.

Координаты точки будем записывать в скобках рядом с буквенным обозначением точки, например: А (х; у) (на первом месте абсцисса, на втором — ордината).

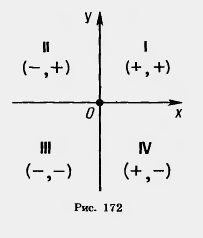
Оси координат разбивают плоскость на четыре части — четверти: I, II, III, IV (рис. 172). В пределах одной четверти знаки обеих координат сохраняются и имеют значения, указанные на рисунке.

 
Точки оси X (оси абсцисс) имеют равные нулю ординаты 9у = 0), а точки оси у (оси ординат) имеют равные нулю абсциссы (х=0). У начала координат абсцисса  и  ордината  равны  нулю.

Плоскость, на которой введены описанным выше способом координаты хну, будем называть плоскостью ху. Произвольную точку на этой плоскости с координатами XVI у будем иногда обозначать просто (х; у). Введенные на плоскости координаты xw.y называются декартовыми по имени Р. Декарта, который впервые применил их в своих исследованиях.

Задача (9). Даны точки А ( — 3; 2) и В (4; 1). Докажите, что отрезок АВ пересекает ось у, но не пересекает ось x.

Решение. Ось у разбивает плоскость ху на две полуплоскости. В одной полуплоскости абсциссы точек положительны, а в другой — отрицательны. Так как у точек А и В абсциссы противоположных знаков, то точки А и В лежат в разных полуплоскостях. А это значит, что отрезок АВ пересекает ось у.

Ось x также разбивает плоскость ху на две полуплоскости. В одной полуплоскости ординаты точек положительны, а в другой — отрицательны. У точек А и В ординаты одного знака (положительны). Значит, точки А и В лежат в одной полуплоскости. А следовательно, отрезок АВ не пересекается с осью х.
 

А. В. Погорелов, Геометрия для 7-11 классов, Учебник для общеобразовательных учреждений

_{онлайн библиотека с учебниками и книгами, планы конспектов уроков по математике, задания по математике 8 класса скачать}

Содержание урока
 конспект урока                       
 опорный каркас  
 презентация урока
 акселеративные методы 
 интерактивные технологии 

Практика
 задачи и упражнения 
 самопроверка
 практикумы, тренинги, кейсы, квесты
 домашние задания
 дискуссионные вопросы
 риторические вопросы от учеников
 
Иллюстрации
 аудио-, видеоклипы и мультимедиа 
 фотографии, картинки 
 графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты

Дополнения
 рефераты
 статьи 
 фишки для любознательных 
 шпаргалки 
 учебники основные и дополнительные
 словарь терминов                          
 прочие 

Совершенствование учебников и уроков
 исправление ошибок в учебнике
 обновление фрагмента в учебнике 
 элементы новаторства на уроке 
 замена устаревших знаний новыми 
 
Только для учителей
 идеальные уроки 
 календарный план на год  
 методические рекомендации  
 программы
 обсуждения


Интегрированные уроки

Если у вас есть исправления или предложения к данному уроку, напишите нам.

Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.