Версия 18:23, 22 июня 2010

Гипермаркет знаний>>Математика>>Математика 8 класс>>Математика: Существование и единственность параллельного переноса

                              СУЩЕСТВОВАНИЕ И ЕДИНСТВЕННОСТЬ ПАРАЛЛЕЛЬНОГО ПЕРЕНОСА

Теорема 9.4.Каковы бы ни были две точки А и А', существует один и только один параллельный перенос, при котором, точка А переходит в точку А'.

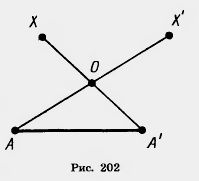
Доказательство. Начнем с доказательства существования параллельного переноса, переводящего точку А в А'. Введем декартовы координаты на плоскости. Пусть a₁, a₂—координаты точки А и a'₁, a'₂ — координаты точки А'. Параллельный перенос, заданный формулами

х' = х +a'₁ — а₁, у' = у + a'₂—а₂,

переводит точку А в точку А'. Действительно, при х = а₁ и у =  a₂ получаем х' = a'₁, у'= a'₂.

Докажем единственность параллельного переноса, переводящего точку А в точку А'. Пусть X — произвольная точка фигуры и X' — точка, в которую она переходит при параллельном переносе (рис. 202). Как мы знаем, отрезки ХА' и АХ' имеют общую середину О. Задание точки X однозначно определяет точку О — середину отрезка А 'X. А точки А к О однозначно определяют точку X', так как точка О является серединой отрезка АХ'. Однозначность в определении точки X' и означает единственность параллельного переноса.

Теорема доказана полностью.

Задача (30). При параллельном переносе точка (1; 1) переходит в точку ( — 1; 0). В какую точку переходит начало координат?

Решение. Любой параллельный перенос задается формулами
х' = х + а, у' = у + b.

Так как точка (1; 1) переходит в точку ( —1;0), то — 1 = 1 + 0, 0 = 1 + b. Отсюда a=—2,  b=—1. Таким образом, наш параллельный перенос, переводящий точку (1; 1) в ( — 1; 0), задается формулами х' = х — 2, у' = у — 1. Подставляя в эти формулы координаты начала (х = 0, y=0), получим х' = —2, у' = — 1. Итак, начало координат переходит в точку ( — 2; —1).

А. В. Погорелов, Геометрия для 7-11 классов, Учебник для общеобразовательных учреждений

_{Материалы по математике за 8 класс скачать, конспект по математике , учебники и книги скатать бесплатно, школьная программа онлайн}

Содержание урока
 конспект урока                       
 опорный каркас  
 презентация урока
 акселеративные методы 
 интерактивные технологии 

Практика
 задачи и упражнения 
 самопроверка
 практикумы, тренинги, кейсы, квесты
 домашние задания
 дискуссионные вопросы
 риторические вопросы от учеников
 
Иллюстрации
 аудио-, видеоклипы и мультимедиа 
 фотографии, картинки 
 графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты

Дополнения
 рефераты
 статьи 
 фишки для любознательных 
 шпаргалки 
 учебники основные и дополнительные
 словарь терминов                          
 прочие 

Совершенствование учебников и уроков
 исправление ошибок в учебнике
 обновление фрагмента в учебнике 
 элементы новаторства на уроке 
 замена устаревших знаний новыми 
 
Только для учителей
 идеальные уроки 
 календарный план на год  
 методические рекомендации  
 программы
 обсуждения


Интегрированные уроки

Если у вас есть исправления или предложения к данному уроку, напишите нам.

Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.