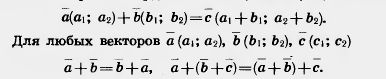|
Версия 06:42, 23 июня 2010
Гипермаркет знаний>>Математика>>Математика 8 класс>>Математика: Сложение векторов
СЛОЖЕНИЕ ВЕКТОРОВ
Суммой векторов  и b с координатами a1, a2 и b1, b2 называется вектор с с координатами а1 + Ь1, a2 + b2. т. е. и b с координатами a1, a2 и b1, b2 называется вектор с с координатами а1 + Ь1, a2 + b2. т. е.
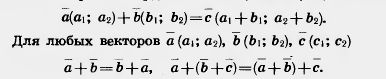
Для доказательства достаточно сравнить соответствующие координаты векторов, стоящих в правой и левой частях равенств. Мы видим, что они равны. А векторы с соответственно равными координатами равны.
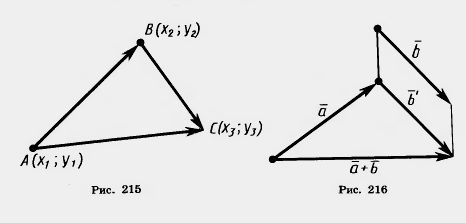
Теорема 10.1. Каковы, бы ни были точки А, В, С, имеет место векторное равенство
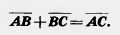
Доказательство. Пусть А (x1; у1), В (x2; у2), С (x3; у3) — данные точки (рис. 215). Вектор  имеет координаты x2 — х1, y2 — y1, вектор имеет координаты x2 — х1, y2 — y1, вектор 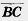 имеет координаты x3 — х2, y3 —y2 Следовательно, вектор имеет координаты x3 — х2, y3 —y2 Следовательно, вектор  + + 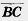 имеет координаты x3 — х1, y3 —y1. А это есть координаты вектора имеет координаты x3 — х1, y3 —y1. А это есть координаты вектора 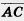 . Значит, . Значит,
векторы  + + 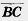 и и 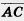 равны. Теорема доказана. равны. Теорема доказана.
Теорема 10.1 дает следующий способ построения суммы произвольных векторов  и и  . Надо от конца вектора а отложить вектор . Надо от конца вектора а отложить вектор  ', равный вектору ', равный вектору  . Тогда вектор, начало которого совпадает с началом вектора . Тогда вектор, начало которого совпадает с началом вектора  , а конец — с концом вектора , а конец — с концом вектора  ' будет суммой векторов ' будет суммой векторов  и и  (рис. 216). Такой способ получения суммы двух векторов называется «правилом треугольника» сложения векторов. (рис. 216). Такой способ получения суммы двух векторов называется «правилом треугольника» сложения векторов.
Для векторов с общим началом их сумма изображается диагональю параллелограмма, построенного на этих векторах («правило параллелограмма», рис. 217). Действительно, 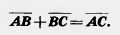 , а , а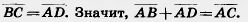
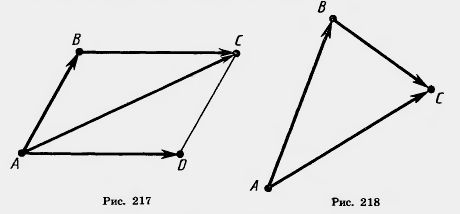
Задача (11). Даны векторы с общим началом:
 и и 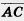 (рис. 218). Докажите, что (рис. 218). Докажите, что 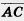 — —  = =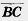 . .
Решение. Имеем  + + 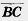 = =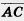 . А это значит, что . А это значит, что 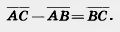
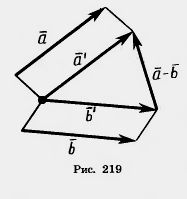
Отсюда получается следующее правило для построения разности двух векторов. Чтобы построить вектор, равный разности векторов  и и  , надо отложить равные им векторы , надо отложить равные им векторы  ' и ' и  ' от одной точки. Тогда вектор, начало которого совпадает с концом вектора ' от одной точки. Тогда вектор, начало которого совпадает с концом вектора  ', а конец — с концом вектора ', а конец — с концом вектора  ', будет разностью векторов ', будет разностью векторов  и и  (рис. 219). (рис. 219).
А. В. Погорелов, Геометрия для 7-11 классов, Учебник для общеобразовательных учреждений
Математика за 8 класс бесплатно скачать, планы конспектов уроков, готовимся к школе онлайн
Содержание урока
 конспект урока конспект урока
 опорный каркас опорный каркас
 презентация урока презентация урока
 акселеративные методы акселеративные методы
 интерактивные технологии
Практика интерактивные технологии
Практика
 задачи и упражнения задачи и упражнения
 самопроверка самопроверка
 практикумы, тренинги, кейсы, квесты практикумы, тренинги, кейсы, квесты
 домашние задания домашние задания
 дискуссионные вопросы дискуссионные вопросы
 риторические вопросы от учеников
Иллюстрации риторические вопросы от учеников
Иллюстрации
 аудио-, видеоклипы и мультимедиа аудио-, видеоклипы и мультимедиа
 фотографии, картинки фотографии, картинки
 графики, таблицы, схемы графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты
Дополнения притчи, поговорки, кроссворды, цитаты
Дополнения
 рефераты рефераты
 статьи статьи
 фишки для любознательных фишки для любознательных
 шпаргалки шпаргалки
 учебники основные и дополнительные учебники основные и дополнительные
 словарь терминов словарь терминов
 прочие
Совершенствование учебников и уроков прочие
Совершенствование учебников и уроков
 исправление ошибок в учебнике исправление ошибок в учебнике
 обновление фрагмента в учебнике обновление фрагмента в учебнике
 элементы новаторства на уроке элементы новаторства на уроке
 замена устаревших знаний новыми
Только для учителей замена устаревших знаний новыми
Только для учителей
 идеальные уроки идеальные уроки
 календарный план на год календарный план на год
 методические рекомендации методические рекомендации
 программы программы
 обсуждения
Интегрированные уроки обсуждения
Интегрированные уроки
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.
|