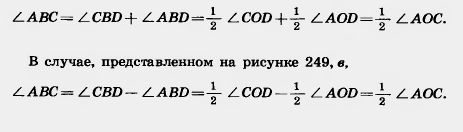Версия 08:44, 24 июня 2010

Гипермаркет знаний>>Математика>>Математика 9 класс>>Математика: Углы, вписанные в окружность

                                          УГЛЫ, ВПИСАННЫЕ В ОКРУЖНОСТЬ

Угол разбивает плоскость на две части. Каждая из частей называется плоским углом. На рисунке 245 заштрихован один из плоских углов со сторонами а и b. Плоские углы с общими сторонами называются дополнительными.

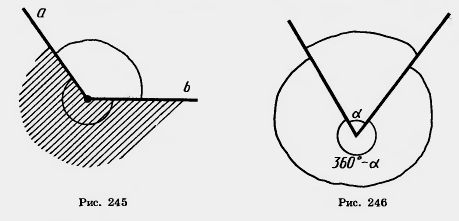
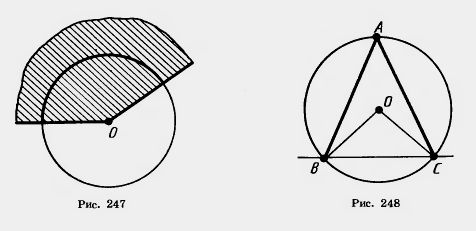
Если плоский угол является частью полуплоскости, то его градусной мерой называется градусная мера обычного угла с теми же сторонами. Если плоский угол содержит полуплоскость, то его градусная мера принимается равной 360° — а, где а — градусная мера дополнительного плоского угла (рис. 246).

 
Центральным углом в окружности называется плоский угол с вершиной в ее центре. Часть окружности, расположенная внутри плоского угла, называется дугой окружности, соответствующей этому центральному углу (рис. 247). Градусной мерой дуги окружности называется градусная мера соответствующего центрального угла.
 

 
Угол, вершина которого лежит на окружности, а стороны пересекают эту окружность,называется вписанным в окружность. Угол ВАС на рисунке 248 вписан в окружность. Его вершина А лежит на окружности, а стороны пересекают окружность в точках В и С. Говорят также, что угол А опирается на хорду ВС.

Прямая ВС разбивает окружность на две дуги. Центральный угол, соответствующий той из этих дуг, которая не содержит точку А, называется центральным углом, соответствующим данному вписанному углу.

Теорема 11.5. Угол, вписанный в окружность, равен половине соаггветствующего центрального угла.

Доказательство. Рассмотрим сначала частный случай, когда одна из сторон угла проходит через центр окружности (рис. 249, а). Треугольник АОВ равнобедренный, так как у него стороны OA и ОВ равны как радиусы. Поэтому углы А и В треугольника равны. А так как их сумма равна внешнему углу треугольника при вершине О, то угол В треугольника равен половине угла АОС, что и требовалось доказать.

 
Общий случай сводится к рассмотренному частному случаю проведением вспомогательного диаметра BD (рис. 249, б, в). В случае, представленном на рисунке 249, б,

Теорема доказана полностью.

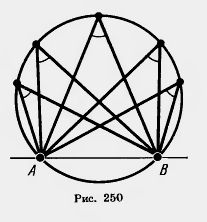
Из теоремы 11.5 следует, что вписанные углы, стороны которых проходят через точки А и В окружности, а вершины лежат по одну сторону от прямой АВ, равны (рис. 250).

В частности, углы, опирающиеся на диаметр, прямые.


 

А. В. Погорелов, Геометрия для 7-11 классов, Учебник для общеобразовательных учреждений

_{Школьная библиотека онлайн, учебники и книги по всему предметам, Математика 9 класс скачать}

Содержание урока
 конспект урока                       
 опорный каркас  
 презентация урока
 акселеративные методы 
 интерактивные технологии 

Практика
 задачи и упражнения 
 самопроверка
 практикумы, тренинги, кейсы, квесты
 домашние задания
 дискуссионные вопросы
 риторические вопросы от учеников
 
Иллюстрации
 аудио-, видеоклипы и мультимедиа 
 фотографии, картинки 
 графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты

Дополнения
 рефераты
 статьи 
 фишки для любознательных 
 шпаргалки 
 учебники основные и дополнительные
 словарь терминов                          
 прочие 

Совершенствование учебников и уроков
 исправление ошибок в учебнике
 обновление фрагмента в учебнике 
 элементы новаторства на уроке 
 замена устаревших знаний новыми 
 
Только для учителей
 идеальные уроки 
 календарный план на год  
 методические рекомендации  
 программы
 обсуждения


Интегрированные уроки

Если у вас есть исправления или предложения к данному уроку, напишите нам.

Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.