Версия 10:02, 24 июня 2010

Гипермаркет знаний>>Математика>>Математика 9 класс>>Математика: Теорема косинусов

                                            ТЕОРЕМА КОСИНУСОВ

Теорема 12.1 (теорема косинусов).Квадрат любой стороны треугольника равен сумме квадратов двух других сторон без удвоенного произведения этих сторон на косинус угла между ними.

 
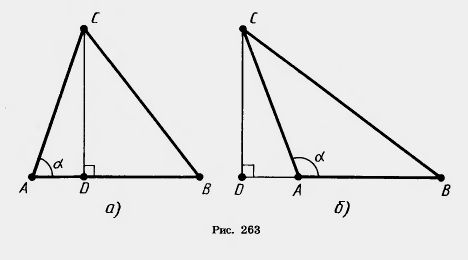
Доказательство. Пусть ABC — данный треугольник (рис. 263). Докажем, что ВС²=АВ²+АС²—2АВ-АС-cosА.
Имеем векторное равенство ВС=АС В. Возводя это равенство скалярно в квадрат, получим:
ВС'=АВ'+АС'-2АВАС,
или
ВС'=АВ^ +АС^-2АВ-АС COS А.
Теорема доказана.
Заметим, что АС • cos А равно по абсолютной величине 
проекции AD стороны АС на сторону АВ (рис. 263, а) или ее 
продолжение (рис. 263, б). Знак АС-cos А зависит от угла А: «-|-»,
если угол А острый, « — », если угол А тупой. Отсюда 
получается следствие: квадрат стороны треугольника равен сумме 
квадратов двух других сторон « + » удвоенное произведение одной
из них на проекцию другой. Знак * + » надо брать, когда
противолежащий угол тупой, а знак «—», когда угол
острый.
Задача (7). Даны стороны треугольника а, Ь, с.
Найдите высоту треугольника, опущенную на сторону с.
Решение. Имеем a' = b' + c'±2c-AD (рис. 264).
Отсюда АВ= ±:° ~^ . По теореме Пифагора
CD=^fAC'-AD'~=-yJ Ь'-[^^^^)\


0 /    \ь
   
D
 

 

А. В. Погорелов, Геометрия для 7-11 классов, Учебник для общеобразовательных учреждений

_{Библиотека с учебниками и книгами на скачку бесплатно онлайн, Математика для 9 класса скачать, школьная программа по математике, планы конспектов уроков}

Содержание урока
 конспект урока                       
 опорный каркас  
 презентация урока
 акселеративные методы 
 интерактивные технологии 

Практика
 задачи и упражнения 
 самопроверка
 практикумы, тренинги, кейсы, квесты
 домашние задания
 дискуссионные вопросы
 риторические вопросы от учеников
 
Иллюстрации
 аудио-, видеоклипы и мультимедиа 
 фотографии, картинки 
 графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты

Дополнения
 рефераты
 статьи 
 фишки для любознательных 
 шпаргалки 
 учебники основные и дополнительные
 словарь терминов                          
 прочие 

Совершенствование учебников и уроков
 исправление ошибок в учебнике
 обновление фрагмента в учебнике 
 элементы новаторства на уроке 
 замена устаревших знаний новыми 
 
Только для учителей
 идеальные уроки 
 календарный план на год  
 методические рекомендации  
 программы
 обсуждения


Интегрированные уроки

Если у вас есть исправления или предложения к данному уроку, напишите нам.

Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.