|
|
|
| Строка 9: |
Строка 9: |
| | <br>В треугольнике против большего угла лежит большая сторона, против большей стороны лежит больший угол. | | <br>В треугольнике против большего угла лежит большая сторона, против большей стороны лежит больший угол. |
| | | | |
| - | Пусть а и b — две стороны треугольника и [[Image:24-06-52.jpg]], [[Image:24-06-53.jpg]] — противолежащие им углы. Докажем, что если а > р, то а > Ь. И обратно: если а>Ъ, то а>р.<br>Если углы аир острые (рис. 267, с), то при а > Р будет sin a>sin p. А так как<br>sin а sin р<br> | + | Пусть а и b — две стороны треугольника и [[Image:24-06-52.jpg]], [[Image:24-06-53.jpg]] — противолежащие им углы. Докажем, что если [[Image:24-06-52.jpg]] > [[Image:24-06-53.jpg]], то а > b. И обратно: если а>b, то [[Image:24-06-52.jpg]]>[[Image:24-06-53.jpg]].<br>Если углы [[Image:24-06-52.jpg]] и [[Image:24-06-53.jpg]] острые (рис. 267, с), то при [[Image:24-06-52.jpg]] > [[Image:24-06-53.jpg]] будет sin [[Image:24-06-52.jpg]]>sin [[Image:24-06-53.jpg]]. А так как<br>sin [[Image:24-06-52.jpg]] sin [[Image:24-06-53.jpg]]<br> |
| | | | |
| - | [[Image:24-06-51.jpg]]<br>Рис. 267<br><br>то а > Ь. Если угол а тупой (оба угла не могут быть тупыми), то угол 180° — а острый (рис. 267, б). Причем угол 180° — а больше угла р как внешний угол треугольника, не смежный с углом р. Поэтому sin а = sin (180° —а) > sin р. И мы снова заключаем, что а>Ъ.<br>Докажем обратное утверждение. Пусть а>Ъ. Надо доказать, что а>р. Допустим, что а^р. Если а = Р, то треугольник равнобедренный и а = Ь. Если а<р, то по доказанному a<ib. В обоих случаях получается противоречие, так как по предположению а>Ь, значит,а>Р, что и требовалось доказать.<br>Задача (17). Докажите, что если в треугольнике есть тупой угол, то противолез4сащая ему сторона наибольшая.<br>Решение. В треугольнике может быть только один тупой угол. Поэтому он больше любого из остальных углов. А значит, противолежащая ему сторона больше любой из двух других сторон треугольника. <br> | + | [[Image:24-06-51.jpg]]<br>Рис. 267<br><br>то а > b. Если угол [[Image:24-06-52.jpg]] тупой (оба угла не могут быть тупыми), то угол 180° — [[Image:24-06-52.jpg]] острый (рис. 267, б). Причем угол 180° — [[Image:24-06-52.jpg]] больше угла [[Image:24-06-53.jpg]] как внешний угол треугольника, не смежный с углом [[Image:24-06-53.jpg]]. Поэтому sin [[Image:24-06-52.jpg]] = sin (180° —а) > sin [[Image:24-06-53.jpg]]. И мы снова заключаем, что а>b. |
| | + | |
| | + | Докажем обратное утверждение. Пусть а>b. Надо доказать, что [[Image:24-06-52.jpg]]>[[Image:24-06-53.jpg]]. Допустим, что [[Image:24-06-52.jpg]][[Image:24-06-54.jpg]][[Image:24-06-53.jpg]]. Если [[Image:24-06-52.jpg]] = [[Image:24-06-53.jpg]], то треугольник равнобедренный и а = b. Если [[Image:24-06-52.jpg]]<[[Image:24-06-53.jpg]], то по доказанному a<b. В обоих случаях получается противоречие, так как по предположению а>Ь, значит,[[Image:24-06-52.jpg]]>[[Image:24-06-53.jpg]], что и требовалось доказать. |
| | + | |
| | + | Задача (17). Докажите, что если в треугольнике есть тупой угол, то противолежащая ему сторона наибольшая. |
| | + | |
| | + | Решение. В треугольнике может быть только один тупой угол. Поэтому он больше любого из остальных углов. А значит, противолежащая ему сторона больше любой из двух других сторон треугольника. <br> |
| | | | |
| | <br> ''А. В. Погорелов, Геометрия для 7-11 классов, Учебник для общеобразовательных учреждений'' <br> | | <br> ''А. В. Погорелов, Геометрия для 7-11 классов, Учебник для общеобразовательных учреждений'' <br> |
Версия 11:02, 24 июня 2010
Гипермаркет знаний>>Математика>>Математика 9 класс>>Математика: Соотношение между углами треугольника и противолежащими сторонами
СООТНОШЕНИЕ МЕЖДУ УГЛАМИ ТРЕУГОЛЬНИКА И ПРОТИВОЛЕЖАЩИМИ СТОРОНАМИ
В треугольнике против большего угла лежит большая сторона, против большей стороны лежит больший угол.
Пусть а и b — две стороны треугольника и  , ,  — противолежащие им углы. Докажем, что если — противолежащие им углы. Докажем, что если  > >  , то а > b. И обратно: если а>b, то , то а > b. И обратно: если а>b, то  > > . .
Если углы  и и  острые (рис. 267, с), то при острые (рис. 267, с), то при  > >  будет sin будет sin  >sin >sin  . А так как . А так как
sin  sin sin 
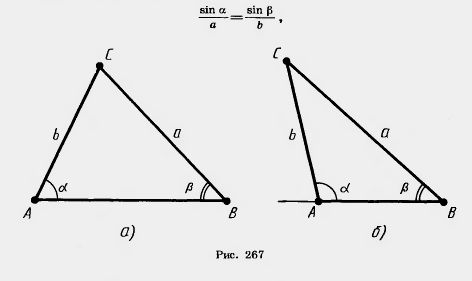
Рис. 267
то а > b. Если угол  тупой (оба угла не могут быть тупыми), то угол 180° — тупой (оба угла не могут быть тупыми), то угол 180° —  острый (рис. 267, б). Причем угол 180° — острый (рис. 267, б). Причем угол 180° —  больше угла больше угла  как внешний угол треугольника, не смежный с углом как внешний угол треугольника, не смежный с углом  . Поэтому sin . Поэтому sin  = sin (180° —а) > sin = sin (180° —а) > sin  . И мы снова заключаем, что а>b. . И мы снова заключаем, что а>b.
Докажем обратное утверждение. Пусть а>b. Надо доказать, что  > > . Допустим, что . Допустим, что    . Если . Если  = =  , то треугольник равнобедренный и а = b. Если , то треугольник равнобедренный и а = b. Если  < < , то по доказанному a<b. В обоих случаях получается противоречие, так как по предположению а>Ь, значит, , то по доказанному a<b. В обоих случаях получается противоречие, так как по предположению а>Ь, значит, > > , что и требовалось доказать. , что и требовалось доказать.
Задача (17). Докажите, что если в треугольнике есть тупой угол, то противолежащая ему сторона наибольшая.
Решение. В треугольнике может быть только один тупой угол. Поэтому он больше любого из остальных углов. А значит, противолежащая ему сторона больше любой из двух других сторон треугольника.
А. В. Погорелов, Геометрия для 7-11 классов, Учебник для общеобразовательных учреждений
Планы конспектов уроков по математике 9 класса скачать, учебники и книги бесплатно, разработки уроков по математике онлайн
Содержание урока
 конспект урока конспект урока
 опорный каркас опорный каркас
 презентация урока презентация урока
 акселеративные методы акселеративные методы
 интерактивные технологии
Практика интерактивные технологии
Практика
 задачи и упражнения задачи и упражнения
 самопроверка самопроверка
 практикумы, тренинги, кейсы, квесты практикумы, тренинги, кейсы, квесты
 домашние задания домашние задания
 дискуссионные вопросы дискуссионные вопросы
 риторические вопросы от учеников
Иллюстрации риторические вопросы от учеников
Иллюстрации
 аудио-, видеоклипы и мультимедиа аудио-, видеоклипы и мультимедиа
 фотографии, картинки фотографии, картинки
 графики, таблицы, схемы графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты
Дополнения притчи, поговорки, кроссворды, цитаты
Дополнения
 рефераты рефераты
 статьи статьи
 фишки для любознательных фишки для любознательных
 шпаргалки шпаргалки
 учебники основные и дополнительные учебники основные и дополнительные
 словарь терминов словарь терминов
 прочие
Совершенствование учебников и уроков прочие
Совершенствование учебников и уроков
 исправление ошибок в учебнике исправление ошибок в учебнике
 обновление фрагмента в учебнике обновление фрагмента в учебнике
 элементы новаторства на уроке элементы новаторства на уроке
 замена устаревших знаний новыми
Только для учителей замена устаревших знаний новыми
Только для учителей
 идеальные уроки идеальные уроки
 календарный план на год календарный план на год
 методические рекомендации методические рекомендации
 программы программы
 обсуждения
Интегрированные уроки обсуждения
Интегрированные уроки
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.
|











