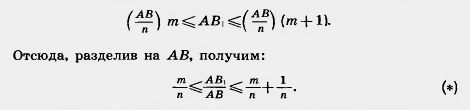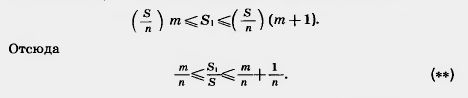Версия 06:36, 29 июня 2010

Гипермаркет знаний>>Математика>>Математика 9 класс>>Математика:Площадь прямоугольника

                                             ПЛОЩАДЬ ПРЯМОУГОЛЬНИКА

Найдем площадь прямоугольника со сторонами а, b. Для этого сначала докажем, что площади двух прямоугольников с равными основаниями относятся как их высоты.

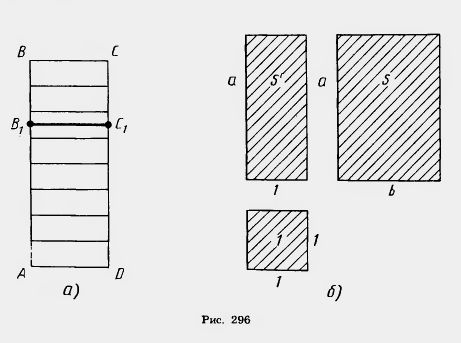
Пусть ABCD и AB₁C₁D — два прямоугольника с общим основанием AD (рис. 296, а). Пусть S и S₁ — их площади. Докажем, что

Разобьем сторону АВ прямоугольника на большое число n равных частей, каждая из них равна   Пусть m — число точек деления, которые лежат на стороне АВ₁. Тогда   

Проведем через точки деления прямые, параллельные основанию AD. Они разобьют прямоугольник ABCD на n равных прямоугольников. Каждый из них имеет площадь   Прямоугольник AB₁C₁D содержит первые т прямоугольников, считая снизу, и содержится в m +1 прямоугольниках. Поэтому

Из неравенств (*) и (**) мы видим, что оба числа заключичены между . Поэтому они отличаются не более чем

 
 
на . А так как n можно взять сколь угодно большим, то это может быть только при , что и требовалось доказать.

Возьмем теперь квадрат, являющийся единицей площади, прямоугольник со сторонами 1, а и прямоугольник со сторонами а, b (рис. 296, б). Сравнивая их площади, по доказанному будем иметь:

Перемножая эти равенства почленно, получим:

S = ab.

Итак, плогцадъ прямоугольника со сторонами а, b вычисляется по формуле S=ab.


 

А. В. Погорелов, Геометрия для 7-11 классов, Учебник для общеобразовательных учреждений

_{Математика за 9 класс бесплатно скачать, планы конспектов уроков, готовимся к школе онлайн}

Содержание урока
 конспект урока                       
 опорный каркас  
 презентация урока
 акселеративные методы 
 интерактивные технологии 

Практика
 задачи и упражнения 
 самопроверка
 практикумы, тренинги, кейсы, квесты
 домашние задания
 дискуссионные вопросы
 риторические вопросы от учеников
 
Иллюстрации
 аудио-, видеоклипы и мультимедиа 
 фотографии, картинки 
 графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты

Дополнения
 рефераты
 статьи 
 фишки для любознательных 
 шпаргалки 
 учебники основные и дополнительные
 словарь терминов                          
 прочие 

Совершенствование учебников и уроков
 исправление ошибок в учебнике
 обновление фрагмента в учебнике 
 элементы новаторства на уроке 
 замена устаревших знаний новыми 
 
Только для учителей
 идеальные уроки 
 календарный план на год  
 методические рекомендации  
 программы
 обсуждения


Интегрированные уроки

Если у вас есть исправления или предложения к данному уроку, напишите нам.

Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.