Задачи-4(9-класс) — Гипермаркет знаний

KNOWLEDGE HYPERMARKET

Задачи-4(9-класс)

 		Версия 08:09, 29 июня 2010 (просмотреть исходный код)
User16  (Обсуждение | вклад)
 (Создана новая страница размером <metakeywords>Гипермаркет Знаний - первый в мире!, Гипермаркет Знаний, Математика, ...)
← Предыдущая правка
		Версия 08:26, 29 июня 2010 (просмотреть исходный код)
User16  (Обсуждение | вклад) 
Следующая правка →
		
Строка 5:
Строка 5:
 <br>    <br>  
  
- '''&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp; ЗАДАЧИ'''<br>&nbsp;<br>122<br><br>2.<br><br>3. 4.<br>&nbsp;<br>1. Докажите, что сумма площадей квадратов, построенных на катетах прямоугольного треугольника, равна площади квадрата, построенного на гипотенузе (рис. 308). <br> + '''&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp; ЗАДАЧИ'''<br>&nbsp;<br>&nbsp;<br>1. Докажите, что сумма площадей квадратов, построенных на катетах прямоугольного треугольника, равна площади квадрата, построенного на гипотенузе (рис. 308). <br>  
  
- [[Image:29-06-62.jpg]] + [[Image:29-06-62.jpg]]  
  
- 2.Стороны двух участков земли квадратной формы равны 100 м и 150 м. Найдите сторону квадратного участка, равновеликого им. + 2.Стороны двух участков земли квадратной формы равны 100 м и 150 м. Найдите сторону квадратного участка, равновеликого им.  
  
- 3.Найдите площадь квадрата S по его диагонали а. + 3.Найдите площадь квадрата S по его диагонали а.  
  
- 4.Во сколько раз площадь квадрата, описанного около окружности, больше площади квадрата, вписанного в ту же окружность? + 4.Во сколько раз площадь квадрата, описанного около окружности, больше площади квадрата, вписанного в ту же окружность?  
  
- 5.Как изменится площадь квадрата, если каждую его сторону увеличить в 3 раза? + 5.Как изменится площадь квадрата, если каждую его сторону увеличить в 3 раза?  
  
- 6.Во сколько раз надо уменьшить стороны квадрата, чтобы его площадь уменьшилась в 25 раз? + 6.Во сколько раз надо уменьшить стороны квадрата, чтобы его площадь уменьшилась в 25 раз?  
  
- 7. Чему равны стороны прямоугольника, если они относятся как 4:9, а его площадь 144 м<sup>2</sup>? + 7. Чему равны стороны прямоугольника, если они относятся как 4:9, а его площадь 144 м<sup>2</sup>?  
  
- 8. Чему равны стороны прямоугольника, если его периметр 74 дм, а&nbsp; площадь 3 м<sup>2</sup>? + 8. Чему равны стороны прямоугольника, если его периметр 74 дм, а&nbsp; площадь 3 м<sup>2</sup>?  
  
- 9. Параллелограмм и прямоугольник имеют одинаковые стороны. Найдите острый угол параллелограмма, если площадь его равна половине площади прямоугольника. + 9. Параллелограмм и прямоугольник имеют одинаковые стороны. Найдите острый угол параллелограмма, если площадь его равна половине площади прямоугольника.  
  
- 10.&nbsp;&nbsp;&nbsp; Квадрат и ромб имеют одинаковые периметры. Какая из фигур имеет большую площадь? Объясните ответ. + 10.&nbsp;&nbsp;&nbsp; Квадрат и ромб имеют одинаковые периметры. Какая из фигур имеет большую площадь? Объясните ответ.  
  
- 11.&nbsp;&nbsp;&nbsp; Найдите площадь ромба, если его высота 10 см, а острый угол 30°. + 11.&nbsp;&nbsp;&nbsp; Найдите площадь ромба, если его высота 10 см, а острый угол 30°.  
  
- 12.&nbsp;&nbsp;&nbsp; Найдите площадь ромба, если его высота 12 см, а меньшая диагональ 13 см. + 12.&nbsp;&nbsp;&nbsp; Найдите площадь ромба, если его высота 12 см, а меньшая диагональ 13 см.  
  
- 13.&nbsp;&nbsp;&nbsp; Докажите, что площадь ромба равна половине произведения диагоналей. + 13.&nbsp;&nbsp;&nbsp; Докажите, что площадь ромба равна половине произведения диагоналей.  
  
- 14.&nbsp;&nbsp;&nbsp; Найдите стороны ромба, зная, что его диагонали относятся как 1 : 2, а площадь ромба равна 12 см<sup>2</sup>. + 14.&nbsp;&nbsp;&nbsp; Найдите стороны ромба, зная, что его диагонали относятся как 1&nbsp;: 2, а площадь ромба равна 12 см<sup>2</sup>.  
  
- 15. Разделите даный треугольник на три равновеликие части прямыми, проходящими через одну вершину. + 15. Разделите даный треугольник на три равновеликие части прямыми, проходящими через одну вершину.  
  
- 16.* Решите предыдущую задачу, взяв вместо треугольника параллелограмм. + 16.* Решите предыдущую задачу, взяв вместо треугольника параллелограмм.  
  
- 17.&nbsp;&nbsp;&nbsp; Чему равна площадь равнобедренного треугольника, если его основание 120 м, а боковая сторона 100 м? + 17.&nbsp;&nbsp;&nbsp; Чему равна площадь равнобедренного треугольника, если его основание 120 м, а боковая сторона 100 м?  
  
- 18.&nbsp;&nbsp;&nbsp; Найдите площадь равнобедренного прямоугольного треугольника с гипотенузой а. + 18.&nbsp;&nbsp;&nbsp; Найдите площадь равнобедренного прямоугольного треугольника с гипотенузой а.  
  
- 19.&nbsp;&nbsp;&nbsp; У треугольника со сторонами 8 см и 4 см проведены высоты к этим сторонам. Высота, проведенная к стороне 8 см, равна 3 см. Чему равна высота, проведенная к стороне 4 см? + 19.&nbsp;&nbsp;&nbsp; У треугольника со сторонами 8 см и 4 см проведены высоты к этим сторонам. Высота, проведенная к стороне 8 см, равна 3 см. Чему равна высота, проведенная к стороне 4 см?  
  
- 20.&nbsp;&nbsp;&nbsp; Докажите, что стороны треугольника обратно пропорциональны его высотам, т. е. + 20.&nbsp;&nbsp;&nbsp; Докажите, что стороны треугольника обратно пропорциональны его высотам, т. е.  
  
- [[Image:29-06-63.jpg]] + [[Image:29-06-63.jpg]]  
  
- 21.&nbsp;&nbsp;&nbsp; Найдите площадь равностороннего треугольника со стороной а. + 21.&nbsp;&nbsp;&nbsp; Найдите площадь равностороннего треугольника со стороной а.  
  
- 22.&nbsp;&nbsp;&nbsp; Найдите площадь правильного треугольника, вписанного в круг радиуса R. + 22.&nbsp;&nbsp;&nbsp; Найдите площадь правильного треугольника, вписанного в круг радиуса R.  
  
- 23.&nbsp;&nbsp;&nbsp; Найдите площадь прямоугольного треугольника, если его высота делит гипотенузу на отрезки 32 см и 18 см. + 23.&nbsp;&nbsp;&nbsp; Найдите площадь прямоугольного треугольника, если его высота делит гипотенузу на отрезки 32 см и 18 см.  
  
- 24.&nbsp;&nbsp;&nbsp; Чему равны катеты прямоугольного треугольника, если его гипотенуза равна 73 см, а площадь равна 1320 см<sup>2</sup>? + 24.&nbsp;&nbsp;&nbsp; Чему равны катеты прямоугольного треугольника, если его гипотенуза равна 73 см, а площадь равна 1320 см<sup>2</sup>?  
  
- 25.&nbsp;&nbsp;&nbsp; У треугольника ABC АС = а, ВС=b. При каком угле С площадь треугольника будет наибольшей? + 25.&nbsp;&nbsp;&nbsp; У треугольника ABC АС = а, ВС=b. При каком угле С площадь треугольника будет наибольшей?  
  
- 26.&nbsp;&nbsp;&nbsp; Найдите площадь равнобедренного треугольника, у которого боковые стороны равны 1 м, а угол между ними равен 70°. + 26.&nbsp;&nbsp;&nbsp; Найдите площадь равнобедренного треугольника, у которого боковые стороны равны 1 м, а угол между ними равен 70°.  
  
- 27.&nbsp;&nbsp;&nbsp; Найдите площадь параллелограмма, если его стороны 2 м и 3 м, а один из углов равен 70°. + 27.&nbsp;&nbsp;&nbsp; Найдите площадь параллелограмма, если его стороны 2 м и 3 м, а один из углов равен 70°.  
  
 28*. Найдите площадь треугольника по стороне а и прилежащим к ней углам а и (3. 29. Выведите формулу Герона для площади треугольника:    28*. Найдите площадь треугольника по стороне а и прилежащим к ней углам а и (3. 29. Выведите формулу Герона для площади треугольника:  
  
- [[Image:29-06-64.jpg]], где а, b, с — длины сторон треугольника, а р — полупериметр. + [[Image:29-06-64.jpg]], где а, b, с — длины сторон треугольника, а р — полупериметр.  
  
- 30.&nbsp;&nbsp;&nbsp; Найдите площадь треугольника по трем сторонам: 1) 13, + 30.&nbsp;&nbsp;&nbsp; Найдите площадь треугольника по трем сторонам: 1) 13,  
  
- [[Image:29-06-65.jpg]] + [[Image:29-06-65.jpg]]  
  
- 31.&nbsp;&nbsp;&nbsp; Стороны треугольника а, b, с. Найдите высоту треугольника, опущенную на сторону с. + 31.&nbsp;&nbsp;&nbsp; Стороны треугольника а, b, с. Найдите высоту треугольника, опущенную на сторону с.  
  
 32.&nbsp;&nbsp;&nbsp; Боковые стороны треугольника 30 см и 25 см. Найдите высоту треугольника, опущенную на основание, равное:    32.&nbsp;&nbsp;&nbsp; Боковые стороны треугольника 30 см и 25 см. Найдите высоту треугольника, опущенную на основание, равное:  
  
- 1) 25 см; 2) 11 см. + 1) 25 см; 2) 11 см.  
  
- 33.&nbsp;&nbsp;&nbsp; Периметр равнобедренного треугольника равен 64 см, а его боковая сторона на 11 см больше основания. Найдите высоту треугольника, опущенную на боковую сторону. + 33.&nbsp;&nbsp;&nbsp; Периметр равнобедренного треугольника равен 64 см, а его боковая сторона на 11 см больше основания. Найдите высоту треугольника, опущенную на боковую сторону.  
  
- 34.&nbsp;&nbsp;&nbsp; Найдите высоты треугольника, у которого стороны равны 13 см, 14 см и 15 см. + 34.&nbsp;&nbsp;&nbsp; Найдите высоты треугольника, у которого стороны равны 13 см, 14 см и 15 см.  
  
- 35.&nbsp;&nbsp;&nbsp; Найдите высоту треугольника со сторонами [[Image:29-06-66.jpg]] ;1,83 проведенную к стороне [[Image:29-06-67.jpg]]. + 35.&nbsp;&nbsp;&nbsp; Найдите высоту треугольника со сторонами [[Image:29-06-66.jpg]]&nbsp;;1,83 проведенную к стороне [[Image:29-06-67.jpg]].  
  
- 36.&nbsp;&nbsp;&nbsp; Найдите наименьшую высоту треугольника со сторонами: 1) 5, 5, 6; 2) 17, 65, 80 и наибольшую высоту треугольника<br>со сторонами:[[Image:29-06-68.jpg]] + 36.&nbsp;&nbsp;&nbsp; Найдите наименьшую высоту треугольника со сторонами: 1) 5, 5, 6; 2) 17, 65, 80 и наибольшую высоту треугольника<br>со сторонами:[[Image:29-06-68.jpg]]  
  
- 37. Найдите площадь трапеции, у которой параллельные стороны 60 см и 20 см, а непараллельные — 13 см и 37 см. + 37. Найдите площадь трапеции, у которой параллельные стороны 60 см и 20 см, а непараллельные — 13 см и 37 см.  
  
- 38.&nbsp;&nbsp;&nbsp; В равнобокой трапеции основания равны 10 см и 24 см, боковая сторона 25 см. Найдите площадь трапеции. + 38.&nbsp;&nbsp;&nbsp; В равнобокой трапеции основания равны 10 см и 24 см, боковая сторона 25 см. Найдите площадь трапеции.  
  
- 39.&nbsp;&nbsp;&nbsp; В равнобокой трапеции большее основание равно 44 м, боковая сторона 17 м и диагональ 39 м. Найдите площадь трапеции. + 39.&nbsp;&nbsp;&nbsp; В равнобокой трапеции большее основание равно 44 м, боковая сторона 17 м и диагональ 39 м. Найдите площадь трапеции.  
  
- 40.&nbsp;&nbsp;&nbsp; Докажите, что если диагонали четырехугольника пересекаются, то площадь четырехугольника равна половине произведения его диагоналей на синус угла между ними. + 40.&nbsp;&nbsp;&nbsp; Докажите, что если диагонали четырехугольника пересекаются, то площадь четырехугольника равна половине произведения его диагоналей на синус угла между ними.  
  
- 41*. Докажите, что среди всех параллелограммов с данными диагоналями наибольшую площадь имеет ромб. + 41*. Докажите, что среди всех параллелограммов с данными диагоналями наибольшую площадь имеет ромб.  
  
- 42. Выведите следующие формулы для радиусов описанной (Д) и вписанной (г) окружностей треугольника:<br>4S&nbsp;&nbsp;&nbsp; а + Ь + с<br>где а, Ь, с — стороны треугольника, а S — его площадь.<br>&nbsp;<br>43- Найдите радиусы описанной (R) и вписанной (г) окружностей для треугольника со сторонами: 1) 13, 14, 15; 2) 15, 13, 4; 3) 35, 29, 8; 4) 4, 5, 7.<br>44.&nbsp;&nbsp;&nbsp; Боковая сторона равнобедренного треугольника 6 см, вы-<br>сота, проведенная к основанию, 4 см. Найдите радиус<br>описанной окружности.<br>45.&nbsp;&nbsp;&nbsp; Найдите радиусы окружностей, описанной около равнобедренного треугольника с основанием а и боковой стороной b и вписанной в него.<br>46.&nbsp;&nbsp;&nbsp; Найдите радиус г вписанной и радиус R описанной окружностей для равнобедренного треугольника с основанием 10 см и боковой стороной 13 см.<br>47.&nbsp;&nbsp;&nbsp; Докажите, что в прямоугольном треугольнике радиус вписанной окружности равен половине разности между суммой катетов и гипотенузой.<br>48.&nbsp;&nbsp;&nbsp; Катеты прямоугольного треугольника равны 40 см и 42 см. Найдите радиусы описанной и вписанной окружностей.<br>49.&nbsp;&nbsp;&nbsp; Докажите, что площадь многоугольника, описанного около окружности, равна половине произведения периметра многоугольника на радиус окружности.<br>128<br>50. Через середину высоты треугольника проведена перпендикулярная к ней прямая. В каком отношении она делит площадь треугольника?<br>51.&nbsp;&nbsp;&nbsp; Прямая, перпендикулярная высоте треугольника, делит<br>его площадь пополам. Найдите расстояние от этой прямой<br>до вершины треугольника, из которой проведена высота,<br>если она равна h.<br>129<br>52.&nbsp;&nbsp;&nbsp; Периметры правильных /г-угольников относятся как а:Ь.<br>Как относятся их площади?<br>53. Найдите площадь круга, если длина окружности /. 54. Найдите площадь кругового кольца (рис. 309), заключенного между двумя окружностями с одним и тем же центром и радиусами: 1) 4 см и 6 см; 2) 5,5 м и 6,5 м; 3) а и Ь, а&gt; Ъ.<br>&nbsp;<br><br>&nbsp;<br><br>&nbsp;<br>55.&nbsp;&nbsp;&nbsp; Во СКОЛЬКО раз увеличится площадь круга, если его диаметр увеличить: 1) в 2 раза; 2) в 5 раз; 3) в m раз?<br>56.&nbsp;&nbsp;&nbsp; Найдите отношение площади круга к площади вписанного в него: 1) квадрата; 2) правильного треугольника; 3) правильного шестиугольника.<br>57.&nbsp;&nbsp;&nbsp; Найдите отношение площади круга, вписанного в правильный треугольник, к площади круга, описанного около него.<br>58.&nbsp;&nbsp;&nbsp; Найдите отношение площади круга, описанного около квадрата, к площади круга, вписанного в него.<br>59.&nbsp;&nbsp;&nbsp; Найдите площадь сектора круга радиуса R, если соответствующий этому сектору центральный угол равен: 1) 40"; 2) 90"; 3) 150"; 4) 240"; 5) 300°; 6) 330".<br>60.&nbsp;&nbsp;&nbsp; Дана окружность радиуса R. Найдите площадь сектора, соответствующего дуге с длиной, равной: 1) R; 2) /.<br>61*. Найдите площадь кругового сегмента с основанием а \ 3<br>и высотой -~г-.<br>62. Найдите площадь той части круга, которая расположена вне вписанного в него: 1) квадрата; 2) правильного треугольника; 3) правильного шестиугольника. Радиус круга R (рис. 310).<br>&nbsp;<br><br>&nbsp;<br>&nbsp; + 42. Выведите следующие формулы для радиусов описанной (R<sub>1</sub>) и вписанной (г) окружностей треугольника:
  +  
  + [[Image:29-06-69.jpg]]<br><br>где а, b, с — стороны треугольника, а S — его площадь.
  +  
  + 43. Найдите радиусы описанной (R) и вписанной (г) окружностей для треугольника со сторонами:
  +  
  + 1) 13, 14, 15; 2) 15, 13, 4; 3) 35, 29, 8; 4) 4, 5, 7.
  +  
  + 44.&nbsp;&nbsp;&nbsp; Боковая сторона равнобедренного треугольника 6 см, высота, проведенная к основанию, 4 см. Найдите радиус описанной окружности.
  +  
  + 45.&nbsp;&nbsp;&nbsp; Найдите радиусы окружностей, описанной около равнобедренного треугольника с основанием а и боковой стороной b и вписанной в него.
  +  
  + 46.&nbsp;&nbsp;&nbsp; Найдите радиус г вписанной и радиус R описанной окружностей для равнобедренного треугольника с основанием 10 см и боковой стороной 13 см.
  +  
  + 47.&nbsp;&nbsp;&nbsp; Докажите, что в прямоугольном треугольнике радиус вписанной окружности равен половине разности между суммой катетов и гипотенузой.
  +  
  + 48.&nbsp;&nbsp;&nbsp; Катеты прямоугольного треугольника равны 40 см и 42 см. Найдите радиусы описанной и вписанной окружностей.
  +  
  + 49.&nbsp;&nbsp;&nbsp; Докажите, что площадь многоугольника, описанного около окружности, равна половине произведения периметра многоугольника на радиус окружности.
  +  
  + 50. Через середину высоты треугольника проведена перпендикулярная к ней прямая. В каком отношении она делит площадь треугольника?
  +  
  + 51.&nbsp;&nbsp;&nbsp; Прямая, перпендикулярная высоте треугольника, делит его площадь пополам. Найдите расстояние от этой прямой до вершины треугольника, из которой проведена высота, если она равна h.
  +  
  + 52.&nbsp;&nbsp;&nbsp; Периметры правильных /г-угольников относятся как а:b. Как относятся их площади?
  +  
  + 53. Найдите площадь круга, если длина окружности l.
  +  
  + 54. Найдите площадь кругового кольца (рис. 309), заключенного между двумя окружностями с одним и тем же центром и радиусами:
  +  
  + 1) 4 см и 6 см; 2) 5,5 м и 6,5 м; 3) а и b, а&gt; b.
  +  
  +  
  +  
  + [[Image:29-06-70.jpg]]
  +  
  +  
  +  
  + 55.&nbsp;&nbsp;&nbsp; Во сколько раз увеличится площадь круга, если его диаметр увеличить:
  +  
  + 1) в 2 раза; 2) в 5 раз; 3) в m раз?
  +  
  + 56.&nbsp;&nbsp;&nbsp; Найдите отношение площади круга к площади вписанного в него:  
  +  
  + 1) квадрата; 2) правильного треугольника; 3) правильного шестиугольника.
  +  
  + 57.&nbsp;&nbsp;&nbsp; Найдите отношение площади круга, вписанного в правильный треугольник, к площади круга, описанного около него.
  +  
  + 58.&nbsp;&nbsp;&nbsp; Найдите отношение площади круга, описанного около квадрата, к площади круга, вписанного в него.
  +  
  + 59.&nbsp;&nbsp;&nbsp; Найдите площадь сектора круга радиуса R, если соответствующий этому сектору центральный угол равен:
  +  
  + 1) 40°; 2) 90°; 3) 150°; 4) 240°; 5) 300°; 6) 330°.
  +  
  + 60.&nbsp;&nbsp;&nbsp; Дана окружность радиуса R. Найдите площадь сектора, соответствующего дуге с длиной, равной:
  +  
  + 1) R; 2) l.
  +  
  + 61*. Найдите площадь кругового сегмента с основанием а \ 3 и высотой [[Image:29-06-38.jpg]].<br>62. Найдите площадь той части круга, которая расположена вне вписанного в него:
  +  
  + 1) квадрата; 2) правильного треугольника; 3) правильного шестиугольника. Радиус круга R (рис. 310).<br>&nbsp;<br>[[Image:29-06-71.jpg]]<br>&nbsp;<br>&nbsp;  
  
 <br> ''А. В. Погорелов, Геометрия для 7-11 классов, Учебник для общеобразовательных учреждений'' <br>    <br> ''А. В. Погорелов, Геометрия для 7-11 классов, Учебник для общеобразовательных учреждений'' <br>  

Версия 08:26, 29 июня 2010
 
Гипермаркет знаний>>Математика>>Математика 9 класс>>Математика:Задачи-4(9-класс) 

 
                                                                        ЗАДАЧИ
 
 
1. Докажите, что сумма площадей квадратов, построенных на катетах прямоугольного треугольника, равна площади квадрата, построенного на гипотенузе (рис. 308). 
 
 
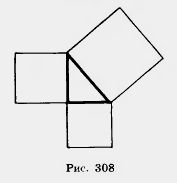
2.Стороны двух участков земли квадратной формы равны 100 м и 150 м. Найдите сторону квадратного участка, равновеликого им. 
3.Найдите площадь квадрата S по его диагонали а. 
4.Во сколько раз площадь квадрата, описанного около окружности, больше площади квадрата, вписанного в ту же окружность? 
5.Как изменится площадь квадрата, если каждую его сторону увеличить в 3 раза? 
6.Во сколько раз надо уменьшить стороны квадрата, чтобы его площадь уменьшилась в 25 раз? 
7. Чему равны стороны прямоугольника, если они относятся как 4:9, а его площадь 144 м²? 
8. Чему равны стороны прямоугольника, если его периметр 74 дм, а  площадь 3 м²? 
9. Параллелограмм и прямоугольник имеют одинаковые стороны. Найдите острый угол параллелограмма, если площадь его равна половине площади прямоугольника. 
10.    Квадрат и ромб имеют одинаковые периметры. Какая из фигур имеет большую площадь? Объясните ответ. 
11.    Найдите площадь ромба, если его высота 10 см, а острый угол 30°. 
12.    Найдите площадь ромба, если его высота 12 см, а меньшая диагональ 13 см. 
13.    Докажите, что площадь ромба равна половине произведения диагоналей. 
14.    Найдите стороны ромба, зная, что его диагонали относятся как 1 : 2, а площадь ромба равна 12 см². 
15. Разделите даный треугольник на три равновеликие части прямыми, проходящими через одну вершину. 
16.* Решите предыдущую задачу, взяв вместо треугольника параллелограмм. 
17.    Чему равна площадь равнобедренного треугольника, если его основание 120 м, а боковая сторона 100 м? 
18.    Найдите площадь равнобедренного прямоугольного треугольника с гипотенузой а. 
19.    У треугольника со сторонами 8 см и 4 см проведены высоты к этим сторонам. Высота, проведенная к стороне 8 см, равна 3 см. Чему равна высота, проведенная к стороне 4 см? 
20.    Докажите, что стороны треугольника обратно пропорциональны его высотам, т. е. 
 
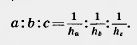
21.    Найдите площадь равностороннего треугольника со стороной а. 
22.    Найдите площадь правильного треугольника, вписанного в круг радиуса R. 
23.    Найдите площадь прямоугольного треугольника, если его высота делит гипотенузу на отрезки 32 см и 18 см. 
24.    Чему равны катеты прямоугольного треугольника, если его гипотенуза равна 73 см, а площадь равна 1320 см²? 
25.    У треугольника ABC АС = а, ВС=b. При каком угле С площадь треугольника будет наибольшей? 
26.    Найдите площадь равнобедренного треугольника, у которого боковые стороны равны 1 м, а угол между ними равен 70°. 
27.    Найдите площадь параллелограмма, если его стороны 2 м и 3 м, а один из углов равен 70°. 
28*. Найдите площадь треугольника по стороне а и прилежащим к ней углам а и (3. 29. Выведите формулу Герона для площади треугольника: 
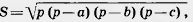, где а, b, с — длины сторон треугольника, а р — полупериметр. 
30.    Найдите площадь треугольника по трем сторонам: 1) 13, 
 
31.    Стороны треугольника а, b, с. Найдите высоту треугольника, опущенную на сторону с. 
32.    Боковые стороны треугольника 30 см и 25 см. Найдите высоту треугольника, опущенную на основание, равное: 
1) 25 см; 2) 11 см. 
33.    Периметр равнобедренного треугольника равен 64 см, а его боковая сторона на 11 см больше основания. Найдите высоту треугольника, опущенную на боковую сторону. 
34.    Найдите высоты треугольника, у которого стороны равны 13 см, 14 см и 15 см. 
35.    Найдите высоту треугольника со сторонами 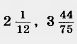 ;1,83 проведенную к стороне . 
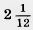36.    Найдите наименьшую высоту треугольника со сторонами: 1) 5, 5, 6; 2) 17, 65, 80 и наибольшую высоту треугольника
со сторонами: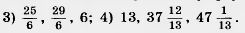 
37. Найдите площадь трапеции, у которой параллельные стороны 60 см и 20 см, а непараллельные — 13 см и 37 см. 
38.    В равнобокой трапеции основания равны 10 см и 24 см, боковая сторона 25 см. Найдите площадь трапеции. 
39.    В равнобокой трапеции большее основание равно 44 м, боковая сторона 17 м и диагональ 39 м. Найдите площадь трапеции. 
40.    Докажите, что если диагонали четырехугольника пересекаются, то площадь четырехугольника равна половине произведения его диагоналей на синус угла между ними. 
41*. Докажите, что среди всех параллелограммов с данными диагоналями наибольшую площадь имеет ромб. 
42. Выведите следующие формулы для радиусов описанной (R₁) и вписанной (г) окружностей треугольника:


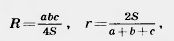
где а, b, с — стороны треугольника, а S — его площадь.
43. Найдите радиусы описанной (R) и вписанной (г) окружностей для треугольника со сторонами:
1) 13, 14, 15; 2) 15, 13, 4; 3) 35, 29, 8; 4) 4, 5, 7.
44.    Боковая сторона равнобедренного треугольника 6 см, высота, проведенная к основанию, 4 см. Найдите радиус описанной окружности.
45.    Найдите радиусы окружностей, описанной около равнобедренного треугольника с основанием а и боковой стороной b и вписанной в него.
46.    Найдите радиус г вписанной и радиус R описанной окружностей для равнобедренного треугольника с основанием 10 см и боковой стороной 13 см.
47.    Докажите, что в прямоугольном треугольнике радиус вписанной окружности равен половине разности между суммой катетов и гипотенузой.
48.    Катеты прямоугольного треугольника равны 40 см и 42 см. Найдите радиусы описанной и вписанной окружностей.
49.    Докажите, что площадь многоугольника, описанного около окружности, равна половине произведения периметра многоугольника на радиус окружности.
50. Через середину высоты треугольника проведена перпендикулярная к ней прямая. В каком отношении она делит площадь треугольника?
51.    Прямая, перпендикулярная высоте треугольника, делит его площадь пополам. Найдите расстояние от этой прямой до вершины треугольника, из которой проведена высота, если она равна h.
52.    Периметры правильных /г-угольников относятся как а:b. Как относятся их площади?
53. Найдите площадь круга, если длина окружности l.
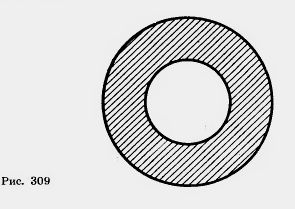
54. Найдите площадь кругового кольца (рис. 309), заключенного между двумя окружностями с одним и тем же центром и радиусами:
1) 4 см и 6 см; 2) 5,5 м и 6,5 м; 3) а и b, а> b.





55.    Во сколько раз увеличится площадь круга, если его диаметр увеличить:
1) в 2 раза; 2) в 5 раз; 3) в m раз?
56.    Найдите отношение площади круга к площади вписанного в него: 
1) квадрата; 2) правильного треугольника; 3) правильного шестиугольника.
57.    Найдите отношение площади круга, вписанного в правильный треугольник, к площади круга, описанного около него.
58.    Найдите отношение площади круга, описанного около квадрата, к площади круга, вписанного в него.
59.    Найдите площадь сектора круга радиуса R, если соответствующий этому сектору центральный угол равен:
1) 40°; 2) 90°; 3) 150°; 4) 240°; 5) 300°; 6) 330°.
60.    Дана окружность радиуса R. Найдите площадь сектора, соответствующего дуге с длиной, равной:
1) R; 2) l.
61*. Найдите площадь кругового сегмента с основанием а \ 3 и высотой .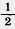
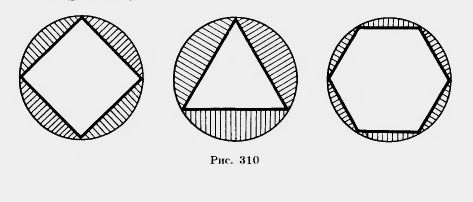
62. Найдите площадь той части круга, которая расположена вне вписанного в него:
1) квадрата; 2) правильного треугольника; 3) правильного шестиугольника. Радиус круга R (рис. 310).
 

 
  

 А. В. Погорелов, Геометрия для 7-11 классов, Учебник для общеобразовательных учреждений 
 
_{Планы конспектов уроков по математике 9 класса скачать, учебники и книги бесплатно, разработки уроков по математике онлайн} 

 

Содержание урока
 конспект урока                       
 опорный каркас  
 презентация урока
 акселеративные методы 
 интерактивные технологии 

Практика
 задачи и упражнения 
 самопроверка
 практикумы, тренинги, кейсы, квесты
 домашние задания
 дискуссионные вопросы
 риторические вопросы от учеников
 
Иллюстрации
 аудио-, видеоклипы и мультимедиа 
 фотографии, картинки 
 графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты

Дополнения
 рефераты
 статьи 
 фишки для любознательных 
 шпаргалки 
 учебники основные и дополнительные
 словарь терминов                          
 прочие 

Совершенствование учебников и уроков
 исправление ошибок в учебнике
 обновление фрагмента в учебнике 
 элементы новаторства на уроке 
 замена устаревших знаний новыми 
 
Только для учителей
 идеальные уроки 
 календарный план на год  
 методические рекомендации  
 программы
 обсуждения


Интегрированные уроки



 
Если у вас есть исправления или предложения к данному уроку, напишите нам. 
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.

Источник — «http://edufuture.biz/index.php?title=%D0%97%D0%B0%D0%B4%D0%B0%D1%87%D0%B8-4(9-%D0%BA%D0%BB%D0%B0%D1%81%D1%81)»
@@ Строка 5: / Строка 5: @@
 <br>
-'''&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp; ЗАДАЧИ'''<br>&nbsp;<br>122<br><br>2.<br><br>3. 4.<br>&nbsp;<br>1. Докажите, что сумма площадей квадратов, построенных на катетах прямоугольного треугольника, равна площади квадрата, построенного на гипотенузе (рис. 308). <br>
+'''&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp; ЗАДАЧИ'''<br>&nbsp;<br>&nbsp;<br>1. Докажите, что сумма площадей квадратов, построенных на катетах прямоугольного треугольника, равна площади квадрата, построенного на гипотенузе (рис. 308). <br>
 [[Image:29-06-62.jpg]]
 .Стороны двух участков земли квадратной формы равны 100 м и 150 м. Найдите сторону квадратного участка, равновеликого им.
 .Найдите площадь квадрата S по его диагонали а.
 .Во сколько раз площадь квадрата, описанного около окружности, больше площади квадрата, вписанного в ту же окружность?
 .Как изменится площадь квадрата, если каждую его сторону увеличить в 3 раза?
 .Во сколько раз надо уменьшить стороны квадрата, чтобы его площадь уменьшилась в 25 раз?
 . Чему равны стороны прямоугольника, если они относятся как 4:9, а его площадь 144 м<sup>2</sup>?
 . Чему равны стороны прямоугольника, если его периметр 74 дм, а&nbsp; площадь 3 м<sup>2</sup>?
 . Параллелограмм и прямоугольник имеют одинаковые стороны. Найдите острый угол параллелограмма, если площадь его равна половине площади прямоугольника.
 .&nbsp;&nbsp;&nbsp; Квадрат и ромб имеют одинаковые периметры. Какая из фигур имеет большую площадь? Объясните ответ.
 .&nbsp;&nbsp;&nbsp; Найдите площадь ромба, если его высота 10 см, а острый угол 30°.
 .&nbsp;&nbsp;&nbsp; Найдите площадь ромба, если его высота 12 см, а меньшая диагональ 13 см.
 .&nbsp;&nbsp;&nbsp; Докажите, что площадь ромба равна половине произведения диагоналей.
-.&nbsp;&nbsp;&nbsp; Найдите стороны ромба, зная, что его диагонали относятся как 1 : 2, а площадь ромба равна 12 см<sup>2</sup>.
+.&nbsp;&nbsp;&nbsp; Найдите стороны ромба, зная, что его диагонали относятся как 1&nbsp;: 2, а площадь ромба равна 12 см<sup>2</sup>.
 . Разделите даный треугольник на три равновеликие части прямыми, проходящими через одну вершину.
 .* Решите предыдущую задачу, взяв вместо треугольника параллелограмм.
 .&nbsp;&nbsp;&nbsp; Чему равна площадь равнобедренного треугольника, если его основание 120 м, а боковая сторона 100 м?
 .&nbsp;&nbsp;&nbsp; Найдите площадь равнобедренного прямоугольного треугольника с гипотенузой а.
 .&nbsp;&nbsp;&nbsp; У треугольника со сторонами 8 см и 4 см проведены высоты к этим сторонам. Высота, проведенная к стороне 8 см, равна 3 см. Чему равна высота, проведенная к стороне 4 см?
 .&nbsp;&nbsp;&nbsp; Докажите, что стороны треугольника обратно пропорциональны его высотам, т. е.
 [[Image:29-06-63.jpg]]
 .&nbsp;&nbsp;&nbsp; Найдите площадь равностороннего треугольника со стороной а.
 .&nbsp;&nbsp;&nbsp; Найдите площадь правильного треугольника, вписанного в круг радиуса R.
 .&nbsp;&nbsp;&nbsp; Найдите площадь прямоугольного треугольника, если его высота делит гипотенузу на отрезки 32 см и 18 см.
 .&nbsp;&nbsp;&nbsp; Чему равны катеты прямоугольного треугольника, если его гипотенуза равна 73 см, а площадь равна 1320 см<sup>2</sup>?
 .&nbsp;&nbsp;&nbsp; У треугольника ABC АС = а, ВС=b. При каком угле С площадь треугольника будет наибольшей?
 .&nbsp;&nbsp;&nbsp; Найдите площадь равнобедренного треугольника, у которого боковые стороны равны 1 м, а угол между ними равен 70°.
 .&nbsp;&nbsp;&nbsp; Найдите площадь параллелограмма, если его стороны 2 м и 3 м, а один из углов равен 70°.
 *. Найдите площадь треугольника по стороне а и прилежащим к ней углам а и (3. 29. Выведите формулу Герона для площади треугольника:
 [[Image:29-06-64.jpg]], где а, b, с — длины сторон треугольника, а р — полупериметр.
 .&nbsp;&nbsp;&nbsp; Найдите площадь треугольника по трем сторонам: 1) 13,
 [[Image:29-06-65.jpg]]
 .&nbsp;&nbsp;&nbsp; Стороны треугольника а, b, с. Найдите высоту треугольника, опущенную на сторону с.
 .&nbsp;&nbsp;&nbsp; Боковые стороны треугольника 30 см и 25 см. Найдите высоту треугольника, опущенную на основание, равное:
 ) 25 см; 2) 11 см.
 .&nbsp;&nbsp;&nbsp; Периметр равнобедренного треугольника равен 64 см, а его боковая сторона на 11 см больше основания. Найдите высоту треугольника, опущенную на боковую сторону.
 .&nbsp;&nbsp;&nbsp; Найдите высоты треугольника, у которого стороны равны 13 см, 14 см и 15 см.
-.&nbsp;&nbsp;&nbsp; Найдите высоту треугольника со сторонами [[Image:29-06-66.jpg]] ;1,83 проведенную к стороне [[Image:29-06-67.jpg]].
+.&nbsp;&nbsp;&nbsp; Найдите высоту треугольника со сторонами [[Image:29-06-66.jpg]]&nbsp;;1,83 проведенную к стороне [[Image:29-06-67.jpg]].
 .&nbsp;&nbsp;&nbsp; Найдите наименьшую высоту треугольника со сторонами: 1) 5, 5, 6; 2) 17, 65, 80 и наибольшую высоту треугольника<br>со сторонами:[[Image:29-06-68.jpg]]
 . Найдите площадь трапеции, у которой параллельные стороны 60 см и 20 см, а непараллельные — 13 см и 37 см.
 .&nbsp;&nbsp;&nbsp; В равнобокой трапеции основания равны 10 см и 24 см, боковая сторона 25 см. Найдите площадь трапеции.
 .&nbsp;&nbsp;&nbsp; В равнобокой трапеции большее основание равно 44 м, боковая сторона 17 м и диагональ 39 м. Найдите площадь трапеции.
 .&nbsp;&nbsp;&nbsp; Докажите, что если диагонали четырехугольника пересекаются, то площадь четырехугольника равна половине произведения его диагоналей на синус угла между ними.
 *. Докажите, что среди всех параллелограммов с данными диагоналями наибольшую площадь имеет ромб.
-. Выведите следующие формулы для радиусов описанной (Д) и вписанной (г) окружностей треугольника:<br>4S&nbsp;&nbsp;&nbsp; а + Ь + с<br>где а, Ь, с — стороны треугольника, а S — его площадь.<br>&nbsp;<br>43- Найдите радиусы описанной (R) и вписанной (г) окружностей для треугольника со сторонами: 1) 13, 14, 15; 2) 15, 13, 4; 3) 35, 29, 8; 4) 4, 5, 7.<br>44.&nbsp;&nbsp;&nbsp; Боковая сторона равнобедренного треугольника 6 см, вы-<br>сота, проведенная к основанию, 4 см. Найдите радиус<br>описанной окружности.<br>45.&nbsp;&nbsp;&nbsp; Найдите радиусы окружностей, описанной около равнобедренного треугольника с основанием а и боковой стороной b и вписанной в него.<br>46.&nbsp;&nbsp;&nbsp; Найдите радиус г вписанной и радиус R описанной окружностей для равнобедренного треугольника с основанием 10 см и боковой стороной 13 см.<br>47.&nbsp;&nbsp;&nbsp; Докажите, что в прямоугольном треугольнике радиус вписанной окружности равен половине разности между суммой катетов и гипотенузой.<br>48.&nbsp;&nbsp;&nbsp; Катеты прямоугольного треугольника равны 40 см и 42 см. Найдите радиусы описанной и вписанной окружностей.<br>49.&nbsp;&nbsp;&nbsp; Докажите, что площадь многоугольника, описанного около окружности, равна половине произведения периметра многоугольника на радиус окружности.<br>128<br>50. Через середину высоты треугольника проведена перпендикулярная к ней прямая. В каком отношении она делит площадь треугольника?<br>51.&nbsp;&nbsp;&nbsp; Прямая, перпендикулярная высоте треугольника, делит<br>его площадь пополам. Найдите расстояние от этой прямой<br>до вершины треугольника, из которой проведена высота,<br>если она равна h.<br>129<br>52.&nbsp;&nbsp;&nbsp; Периметры правильных /г-угольников относятся как а:Ь.<br>Как относятся их площади?<br>53. Найдите площадь круга, если длина окружности /. 54. Найдите площадь кругового кольца (рис. 309), заключенного между двумя окружностями с одним и тем же центром и радиусами: 1) 4 см и 6 см; 2) 5,5 м и 6,5 м; 3) а и Ь, а&gt; Ъ.<br>&nbsp;<br><br>&nbsp;<br><br>&nbsp;<br>55.&nbsp;&nbsp;&nbsp; Во СКОЛЬКО раз увеличится площадь круга, если его диаметр увеличить: 1) в 2 раза; 2) в 5 раз; 3) в m раз?<br>56.&nbsp;&nbsp;&nbsp; Найдите отношение площади круга к площади вписанного в него: 1) квадрата; 2) правильного треугольника; 3) правильного шестиугольника.<br>57.&nbsp;&nbsp;&nbsp; Найдите отношение площади круга, вписанного в правильный треугольник, к площади круга, описанного около него.<br>58.&nbsp;&nbsp;&nbsp; Найдите отношение площади круга, описанного около квадрата, к площади круга, вписанного в него.<br>59.&nbsp;&nbsp;&nbsp; Найдите площадь сектора круга радиуса R, если соответствующий этому сектору центральный угол равен: 1) 40"; 2) 90"; 3) 150"; 4) 240"; 5) 300°; 6) 330".<br>60.&nbsp;&nbsp;&nbsp; Дана окружность радиуса R. Найдите площадь сектора, соответствующего дуге с длиной, равной: 1) R; 2) /.<br>61*. Найдите площадь кругового сегмента с основанием а \ 3<br>и высотой -~г-.<br>62. Найдите площадь той части круга, которая расположена вне вписанного в него: 1) квадрата; 2) правильного треугольника; 3) правильного шестиугольника. Радиус круга R (рис. 310).<br>&nbsp;<br><br>&nbsp;<br>&nbsp;
+. Выведите следующие формулы для радиусов описанной (R<sub>1</sub>) и вписанной (г) окружностей треугольника:
+[[Image:29-06-69.jpg]]<br><br>где а, b, с — стороны треугольника, а S — его площадь.
+. Найдите радиусы описанной (R) и вписанной (г) окружностей для треугольника со сторонами:
+) 13, 14, 15; 2) 15, 13, 4; 3) 35, 29, 8; 4) 4, 5, 7.
+.&nbsp;&nbsp;&nbsp; Боковая сторона равнобедренного треугольника 6 см, высота, проведенная к основанию, 4 см. Найдите радиус описанной окружности.
+.&nbsp;&nbsp;&nbsp; Найдите радиусы окружностей, описанной около равнобедренного треугольника с основанием а и боковой стороной b и вписанной в него.
+.&nbsp;&nbsp;&nbsp; Найдите радиус г вписанной и радиус R описанной окружностей для равнобедренного треугольника с основанием 10 см и боковой стороной 13 см.
+.&nbsp;&nbsp;&nbsp; Докажите, что в прямоугольном треугольнике радиус вписанной окружности равен половине разности между суммой катетов и гипотенузой.
+.&nbsp;&nbsp;&nbsp; Катеты прямоугольного треугольника равны 40 см и 42 см. Найдите радиусы описанной и вписанной окружностей.
+.&nbsp;&nbsp;&nbsp; Докажите, что площадь многоугольника, описанного около окружности, равна половине произведения периметра многоугольника на радиус окружности.
+. Через середину высоты треугольника проведена перпендикулярная к ней прямая. В каком отношении она делит площадь треугольника?
+.&nbsp;&nbsp;&nbsp; Прямая, перпендикулярная высоте треугольника, делит его площадь пополам. Найдите расстояние от этой прямой до вершины треугольника, из которой проведена высота, если она равна h.
+.&nbsp;&nbsp;&nbsp; Периметры правильных /г-угольников относятся как а:b. Как относятся их площади?
+. Найдите площадь круга, если длина окружности l.
+. Найдите площадь кругового кольца (рис. 309), заключенного между двумя окружностями с одним и тем же центром и радиусами:
+) 4 см и 6 см; 2) 5,5 м и 6,5 м; 3) а и b, а&gt; b.
+[[Image:29-06-70.jpg]]
+.&nbsp;&nbsp;&nbsp; Во сколько раз увеличится площадь круга, если его диаметр увеличить:
+) в 2 раза; 2) в 5 раз; 3) в m раз?
+.&nbsp;&nbsp;&nbsp; Найдите отношение площади круга к площади вписанного в него:
+) квадрата; 2) правильного треугольника; 3) правильного шестиугольника.
+.&nbsp;&nbsp;&nbsp; Найдите отношение площади круга, вписанного в правильный треугольник, к площади круга, описанного около него.
+.&nbsp;&nbsp;&nbsp; Найдите отношение площади круга, описанного около квадрата, к площади круга, вписанного в него.
+.&nbsp;&nbsp;&nbsp; Найдите площадь сектора круга радиуса R, если соответствующий этому сектору центральный угол равен:
+) 40°; 2) 90°; 3) 150°; 4) 240°; 5) 300°; 6) 330°.
+.&nbsp;&nbsp;&nbsp; Дана окружность радиуса R. Найдите площадь сектора, соответствующего дуге с длиной, равной:
+) R; 2) l.
+*. Найдите площадь кругового сегмента с основанием а \ 3 и высотой [[Image:29-06-38.jpg]].<br>62. Найдите площадь той части круга, которая расположена вне вписанного в него:
+) квадрата; 2) правильного треугольника; 3) правильного шестиугольника. Радиус круга R (рис. 310).<br>&nbsp;<br>[[Image:29-06-71.jpg]]<br>&nbsp;<br>&nbsp;
 <br> ''А. В. Погорелов, Геометрия для 7-11 классов, Учебник для общеобразовательных учреждений'' <br>

Авторські права | Privacy Policy |FAQ | Партнери | Контакти | Кейс-уроки

© Автор системы образования 7W и Гипермаркета Знаний - Владимир Спиваковский

При использовании материалов ресурса
ссылка на edufuture.biz обязательна (для интернет ресурсов - гиперссылка).
edufuture.biz 2008-© Все права защищены.
Сайт edufuture.biz является порталом, в котором не предусмотрены темы политики, наркомании, алкоголизма, курения и других "взрослых" тем.

Разработка - Гипермаркет знаний 2008-

Ждем Ваши замечания и предложения на email:
По вопросам рекламы и спонсорства пишите на email: