|
|
|
| Строка 1: |
Строка 1: |
| - | <metakeywords>Гипермаркет Знаний - первый в мире!, Гипермаркет Знаний, Математика, 9 класс, Алгебра, урок, на Тему, Построение некоторых правильных многоугольников</metakeywords> | + | <metakeywords>Гипермаркет Знаний - первый в мире!, Гипермаркет Знаний, Математика, 9 класс, Геометрия, урок, на Тему, Построение некоторых правильных многоугольников</metakeywords> |
| | | | |
| | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Математика|Математика]]>>[[Математика 9 класс|Математика 9 класс]]>>Математика:Построение некоторых правильных многоугольников''' | | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Математика|Математика]]>>[[Математика 9 класс|Математика 9 класс]]>>Математика:Построение некоторых правильных многоугольников''' |
Версия 15:43, 29 июня 2010
Гипермаркет знаний>>Математика>>Математика 9 класс>>Математика:Построение некоторых правильных многоугольников
ПОСТРОЕНИЕ НЕКОТОРЫХ ПРАВИЛЬНЫХ МНОГОУГОЛЬНИКОВ
Для построения правильного многоугольника, вписанного в окружность, достаточно построить его центральный угол.
У правильного шестиугольника такой угол равен 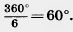
Поэтому для построения правильного шестиугольника одну вершину (A1) на окружности берем произвольно. Из нее как из центра радиусом, равным радиусу окружности, делаем засечку и получаем вершину Аг (рис. 282). Затем аналогично строим остальные вершины А3, А4, А5, A6 и соединяем их отрезками.
Для построения правильного вписанного треугольника достаточно соединить через одну вершины правильного вписанного шестиугольника (рис. 283).
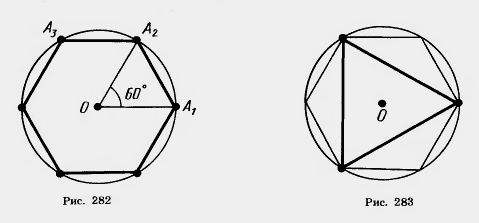
Для построения правильного вписанного четырехугольника (квадрата) достаточно провести через центр окружности перпендикулярные прямые. Они пересекут окружность в вершинах квадрата (рис. 284).
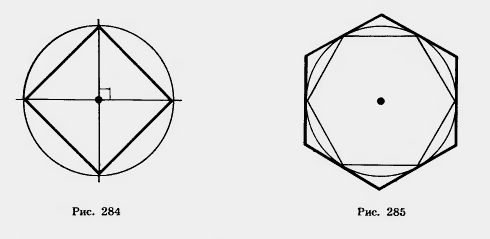
Для построения правильного описанного многоугольника достаточно провести касательные к окружности в вершинах правильного вписанного многоугольника. Касательные, проходящие через вершины правильного вписанного многоугольника, пересекаются в вершинах правильного описанного многоугольника (рис. 285).
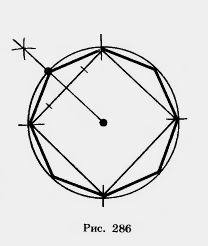
Если в окружность вписан правильный n-угольник, то легко построить правильный вписанный 2n-угольник. На рисунке 286 показано построение правильного восьмиугольника.
А. В. Погорелов, Геометрия для 7-11 классов, Учебник для общеобразовательных учреждений
Учебники по всему предметам скачать, разработка планов уроков для учителей, Математика для 9 класса онлайн
Содержание урока
 конспект урока конспект урока
 опорный каркас опорный каркас
 презентация урока презентация урока
 акселеративные методы акселеративные методы
 интерактивные технологии
Практика интерактивные технологии
Практика
 задачи и упражнения задачи и упражнения
 самопроверка самопроверка
 практикумы, тренинги, кейсы, квесты практикумы, тренинги, кейсы, квесты
 домашние задания домашние задания
 дискуссионные вопросы дискуссионные вопросы
 риторические вопросы от учеников
Иллюстрации риторические вопросы от учеников
Иллюстрации
 аудио-, видеоклипы и мультимедиа аудио-, видеоклипы и мультимедиа
 фотографии, картинки фотографии, картинки
 графики, таблицы, схемы графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты
Дополнения притчи, поговорки, кроссворды, цитаты
Дополнения
 рефераты рефераты
 статьи статьи
 фишки для любознательных фишки для любознательных
 шпаргалки шпаргалки
 учебники основные и дополнительные учебники основные и дополнительные
 словарь терминов словарь терминов
 прочие
Совершенствование учебников и уроков прочие
Совершенствование учебников и уроков
 исправление ошибок в учебнике исправление ошибок в учебнике
 обновление фрагмента в учебнике обновление фрагмента в учебнике
 элементы новаторства на уроке элементы новаторства на уроке
 замена устаревших знаний новыми
Только для учителей замена устаревших знаний новыми
Только для учителей
 идеальные уроки идеальные уроки
 календарный план на год календарный план на год
 методические рекомендации методические рекомендации
 программы программы
 обсуждения
Интегрированные уроки обсуждения
Интегрированные уроки
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.
|













