Версия 15:50, 29 июня 2010

Гипермаркет знаний>>Математика>>Математика 9 класс>>Математика: Задачи-1(9-класс)

                                                                   ЗАДАЧИ

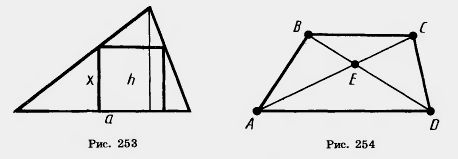
1. При гомотетии точка X переходит в точку X', а точка Y — в точку Y'. Как найти центр гомотетии, если точки X, X', Y, Y' не лежат на одной прямой?

2.    При гомотетии точка X переходит в точку X'. Постройте центр гомотетии, если коэффициент гомотетии равен 2.

3.    Начертите треугольник. Постройте гомотетичный ему треугольник, приняв за центр гомотетии одну из его вершин и коэффициент гомотетии равным 2.

4.    На рисунке 236 изображен план усадьбы в масштабе 1:1000. Определите размеры усадьбы (длину и ширину).

5. Что представляет собой фигура, подобная треугольнику?

6.    У подобных треугольников ABC и А₁В₁С₁ A = 30°, АВ = 1 м, ВС = 2 м, B₁C1=3 м. Чему равны угол А₁ и сторона А₁В₁?

7.    Докажите, что фигура, подобная окружности, есть окружность.

8*. Даны угол и внутри его точка А. Постройте окружность, касающуюся сторон угла и проходящую через точку А.

9*. Впишите в данный треугольник квадрат, у которого две вершины лежат на одной стороне, а две другие вершины — на двух других сторонах.

10. Докажите подобие равнобедренных треугольников с равными углами при вершинах, противолежащих основаниям.

11.    У двух равнобедренных треугольников углы между боковыми сторонами равны. Боковая сторона и основание одного треугольника равны 17 см и 10 см, основание другого равно 8 см. Найдите его боковую сторону.

12.    У треугольников ABC и А₁В₁С₁ ZA=Ai, B=Bi, АВ = 5 м, ВС = 7 м, A,B₁ = 10 м, A₁C₁=8 м. Найдите остальные стороны треугольников.

13.    Решите задачу 12 при условии, что АВ = 16 см, ВС = = 20 см, A₁B₁ = 12 см, АС —A₁С₁ =6 см.

14.    Докажите, что высота прямоугольного треугольника, опущенная из вершины прямого угла, разбивает его на два треугольника, подобные исходному.

15.    Прямая, параллельная стороне АВ треугольника ABC, пересекает его сторону АС в точке A₁, а сторону ВС в точке В₁. Докажите, что

АВС А₁В₁С.

16.    В треугольник с основанием а и высотой h вписан квадрат так, что две его вершины лежат на основании треугольника, а другие две — на боковых сторонах (рис. 253). Вычислите сторону квадрата.

17.    Прямая, параллельная стороне АВ треугольника ABC, делит его сторону АС в отношении т:п, считая от вершины С. В каком отношении она делит сторону ВС?

18.    В треугольнике ABC проведен отрезок DE, параллельный стороне АС (конец D отрезка лежит на стороне АВ, а Е — на стороне ВС). Найдите AD, если АВ=16 см, АС = 20 см и DE=15 см.

19.    В задаче 18 найдите отношение AD:BD, если известно, что AC:DE = 55:28.

20.    Найдите длину отрезка DE в задаче 18, если: 1) АС = = 20 см, АВ = П см и BD = 11,9 см; 2) АС = 18 дм, АВ = 15 дм и AD = 10 дм.

21.    Диагонали трапеции ABCD пересекаются в точке Е (рис. 254). Докажите подобие треугольников ВСЕ и DAE.

 
22.    Найдите отношение отрезков диагонали трапеции, на которые она разбивается другой диагональю, если основания трапеции относятся как m:n.

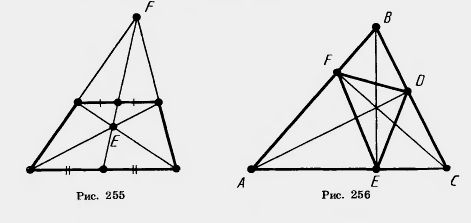
23.    Прямая, проходящая через точку пересечения диагоналей трапеции, делит одно основание в отношении m:n. В каком отношении она делит другое основание?

24.    В трапеции ABCD с диагональю АС углы ABC и ACD равны. Найдите диагональ АС, если основания ВС и AD соответственно равны 12 м и 27 м.

25.    Линия, параллельная основаниям трапеции, делит одну боковую сторону в отношении т:п. В каком отношении делит она другую боковую сторону?

26.    Продолжения боковых сторон АВ и CD трапеции ABCD пересекаются в точке Е. Найдите стороны треугольника AED, если АВ = 5 см, ВС = 10 см, CD = 6 см, AD= 15 см.

27. Найдите высоту треугольника AED из задачи 26, опущенную на сторону AD, если ВС = 7 см, AD = 21 см и высота трапеции равна 3 см.

28*. Диагонали трапеции пересекаются в точке ?, а продолжения боковых сторон — в точке F. Докажите, что прямая EF делит основания трапеции пополам (рис. 255).

29*. У равнобедренного треугольника AВС с основанием АС и противолежащим углом 36° проведена биссектриса AD.

1)    Докажите подобие треугольников ABC и CAD.
2)    Найдите основание треугольника АВС, если его боковая сторона равна а.

30. Углы В и B₁ треугольников ABC и А₁В₁С₁ равны. Стороны треугольника ABC,  прилежащие  к  углу В, в 2,5 раза больше сторон треугольника А₁В₁С₁, прилежащих к углу В₁. Найдите АС и А₁С₁, если их сумма равна 4,2 м.

31. В треугольнике ABC с острым углом С проведены высоты АЕ и BD. Докажите, что ABC EDC.

32*. В остроугольном треугольнике ABC проведены высоты AD, BE, CF. Найдите углы треугольника DEF, зная углы треугольника ABC (рис. 256).

33*. Докажите, что биссектрисы треугольника DEF в задаче 32 лежат на высотах треугольника ABC.

34. Подобны ли два равносторонних треугольника?

35. Подобны ли треугольники ABC и А₁В₁С₁, если:

1)    АВ = 1 м,       АС = 1,5 м,    ВС = 2 м; A,Bi = 10 см, А₁С₁ = 15 см, В₁С₁ = 20 см;
2)    АВ = 1 м,       АС = 2 м,      ВС = 1,5 м; А,В, = 8 дм, А₁С₁ = 16 дм, В₁С₁ = 12 дм;
3)    АВ=1 м,       АС = 2 м,      ВС = 1,25 м; АiB, = 10 см, А₁С₁ = 20 см, В₁С₁ = 13 см?

 
36.    Докажите, что у подобных треугольников периметры относятся как соответствующие стороны.

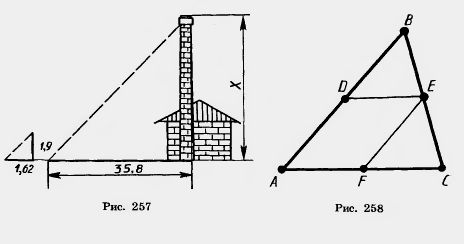
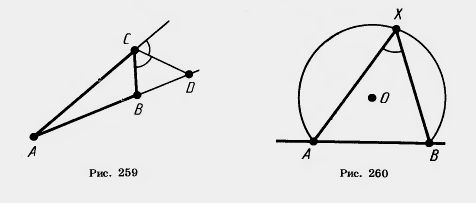
37.    Стороны треугольника равны 0,8 м, 1,6 м и 2 м. Найдите стороны подобного ему треугольника, периметр которого равен 5,5 м.

38. Периметр одного треугольника составляет периметра noдобного ему треугольника. Разность двух соответствующих сторон равна 1 м. Найдите эти стороны.

39. Подобны ли два прямоугольных треугольника, если у одного из них есть угол 40°, а у другого — угол, равный:

1) 50°; 2) 60°?

40.    Основание высоты прямоугольного треугольника, опущенной на гипотенузу, делит ее на отрезки 9 см и 16 см. Найдите стороны треугольника.

41.    Гипотенуза прямоугольного треугольника равна 25 см, а один из катетов равен 10 см. Найдите проекцию другого катета на гипотенузу.

42.    Докажите, что соответствующие высоты подобных треугольников относятся как соответствующие стороны.

43.    Катеты прямоугольного треугольника относятся как т: п. Как относятся проекции катетов на гипотенузу?

44.    Длина тени фабричной трубы равна 35,8 м; в это же время вертикально воткнутый в землю кол высотой 1,9 м дает тень длиной 1,62 м (рис. 257). Найдите высоту трубы.

45.    В треугольник ABC вписан ромб ADEF так, что угол А у них общий, а вершина Е находится на стороне ВС (рис. 258). Найдите сторону ромба, если АВ=с и АС=b.

46*. Биссектриса внешнего угла треугольника ABC при вершине С пересекает прямую АВ в точке D (рис. 259). Докажите, что AD:BD=AC:BC.
 

 
47*. Докажите, что геометрическое место точек, отношение расстояний от которых до двух данных точек постоянно (не равно единице), есть окружность.

48. Найдите дополнительные плоские углы, зная, что:

1) один из них в 5 раз больше другого;

2) один из них на 100° больше другого;

3) разность их равна 20°.

49.    Точки А, В, С лежат на окружности. Чему равна хорда АС, если угол ABC равен 30°, а диаметр окружности 10 см?

50.    Точки А, В, С лежат на окружности. Чему равен угол ABC, если хорда АС равна радиусу окружности? (Два случая.)

51.    Докажите, что центром окружности, описанной около прямоугольного треугольника, является середина гипотенузы.

52.    Докажите, что медиана прямоугольного треугольника, проведенная к гипотенузе, разбивает его на два равнобедренных треугольника.

53.    Постройте прямоугольный треугольник по гипотенузе и высоте, опущенной из вершины прямого угла на гипотенузу.

54.    На окружности отмечены четыре точки А, В, С, D. Чему равен угол ADC, если угол ABC равен а? (Два случая.)

55.    Хорды окружности AD и ВС пересекаются. Угол ABC равен 50°, угол ACD равен 80°. Найдите угол CAD.

56*. Докажите, что у четырехугольника, вписанного в окружность, сумма противолежащих углов равна 180°.

57.    Докажите, что геометрическое место вершин прямых углов, стороны которых проходят через две данные точки, есть окружность.

58.    Докажите, что геометрическое место вершин углов с заданной градусной мерой, стороны которых проходят через две данные точки, а вершины лежат по одну сторону
 

 
от прямой, соединяющей эти точки, есть дуга окружности с концами в этих точках (рис. 260).

59.    Докажите, что острый угол между хордой окружности и касательной к окружности в конце хорды равен половине угла между радиусами, проведенными к концам хорды (рис. 261).

60.    Постройте треугольник по стороне, противолежащему ей углу и высоте, проведенной из вершины этого угла.

61. Из точки С окружности проведен перпендикуляр CD к диаметру АВ. Докажите, что CD²=ADBD.

62. Докажите, что произведение отрезков секущей окружности равно квадрату отрезка касательной, проведенной из той же точки: ACBC = CD² (рис. 262).

 

63.    Как далеко видно из самолета, летящего на высоте 4 км над Землей, если радиус Земли 6370 км?

64.    Вычислите радиус горизонта, видимого с вершины телебашни в Останкине, высота которой 537 м.



 

А. В. Погорелов, Геометрия для 7-11 классов, Учебник для общеобразовательных учреждений

_{Сборник конспектов уроков по математике скачать, календарно-тематическое планирование, учебники по всем предметам онлайн}

Содержание урока
 конспект урока                       
 опорный каркас  
 презентация урока
 акселеративные методы 
 интерактивные технологии 

Практика
 задачи и упражнения 
 самопроверка
 практикумы, тренинги, кейсы, квесты
 домашние задания
 дискуссионные вопросы
 риторические вопросы от учеников
 
Иллюстрации
 аудио-, видеоклипы и мультимедиа 
 фотографии, картинки 
 графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты

Дополнения
 рефераты
 статьи 
 фишки для любознательных 
 шпаргалки 
 учебники основные и дополнительные
 словарь терминов                          
 прочие 

Совершенствование учебников и уроков
 исправление ошибок в учебнике
 обновление фрагмента в учебнике 
 элементы новаторства на уроке 
 замена устаревших знаний новыми 
 
Только для учителей
 идеальные уроки 
 календарный план на год  
 методические рекомендации  
 программы
 обсуждения


Интегрированные уроки

Если у вас есть исправления или предложения к данному уроку, напишите нам.

Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.