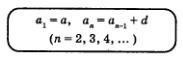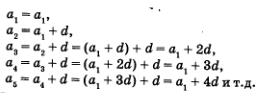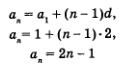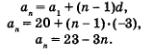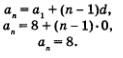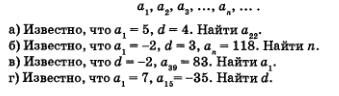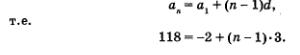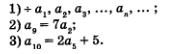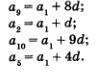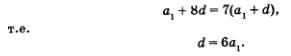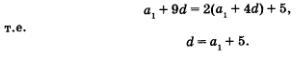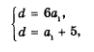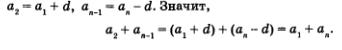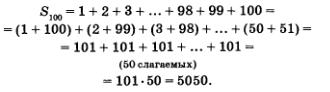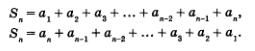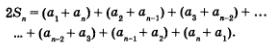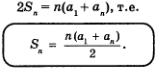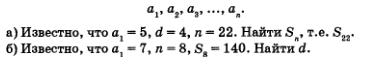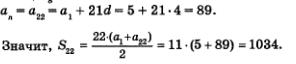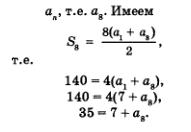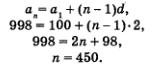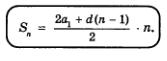|
|
|
| Строка 51: |
Строка 51: |
| | В итоге получаем очень простую систему двух линейных уравнений с двумя переменными а<sub>1</sub> и d: | | В итоге получаем очень простую систему двух линейных уравнений с двумя переменными а<sub>1</sub> и d: |
| | | | |
| - | [[Image:Al91633.jpg]]<br>которая в сочетании с записанным выше условием 1) и представляет собой математическую модель задачи.<br>'''Второй этап. '''Работа с составленной моделью.<br>Решая систему, находим a<sub>1</sub> = 1, d = 6.<br>Теперь мы можем записать арифметическую прогрессию 1,7, 13,19, 25,31,....<br>'''Третий этап.''' Ответ на вопрос задачи.<br>Требуется вычислить а<sub>20</sub>. Имеем [[Image:al91634.jpg]]<br>'''О т в е т:''' а<sub>20</sub> = 115.<br>'''Замечание.''' В рассмотренном примере речь шла о конкретной математической модели — арифметической прогрессии. Первый этап решения мы назвали, как обычно, «составление математической модели». Получается, что мы составили математическую модель для математической модели. Как это понимать? Дело в том, что при решении задач очень часто приходится заменять одну математическую модель другой, более простой. Так обстоит дело и в рассмотренной задаче: математическую модель, оформленную в виде условий 1), 2) и 3), нам удалось заменить более привычной моделью — системой уравнений.<br>'''3.''' Формула суммы членов конечной арифметической прогрессии.<br>Пусть дана конечная арифметическая прогрессия | + | [[Image:Al91633.jpg]]<br>которая в сочетании с записанным выше условием 1) и представляет собой математическую модель задачи.<br>'''Второй этап. '''Работа с составленной моделью.<br>Решая систему, находим a<sub>1</sub> = 1, d = 6.<br>Теперь мы можем записать арифметическую прогрессию 1,7, 13,19, 25,31,....<br>'''Третий этап.''' Ответ на вопрос задачи.<br>Требуется вычислить а<sub>20</sub>. Имеем [[Image:Al91634.jpg]]<br>'''О т в е т:''' а<sub>20</sub> = 115.<br>'''Замечание.''' В рассмотренном примере речь шла о конкретной математической модели — арифметической прогрессии. Первый этап решения мы назвали, как обычно, «составление математической модели». Получается, что мы составили математическую модель для математической модели. Как это понимать? Дело в том, что при решении задач очень часто приходится заменять одну математическую модель другой, более простой. Так обстоит дело и в рассмотренной задаче: математическую модель, оформленную в виде условий 1), 2) и 3), нам удалось заменить более привычной моделью — системой уравнений.<br>'''3.''' Формула суммы членов конечной арифметической прогрессии.<br>Пусть дана конечная арифметическая прогрессия |
| | | | |
| - | [[Image:al01635.jpg]]<br>Обозначим через Sn сумму ее членов, т.е.<br>[[Image:al91636.jpg]]<br>Выведем формулу для нахождения этой суммы.<br>Для начала заметим, что [[Image:al91637.jpg]]<br>В самом деле, по определению арифметической прогрессии, | + | [[Image:Al01635.jpg]]<br>Обозначим через Sn сумму ее членов, т.е.<br>[[Image:Al91636.jpg]]<br>Выведем формулу для нахождения этой суммы.<br>Для начала заметим, что [[Image:Al91637.jpg]]<br>В самом деле, по определению арифметической прогрессии, |
| | | | |
| - | [[Image:al91638.jpg]]<br>Аналогично можно установить, что [[Image:al91639.jpg]] и вообще что сумма члена, находящегося на к-м месте от начала конечной арифметической прогрессии, и члена, находящегося на к-м месте от ее конца, равна сумме первого и последнего членов прогрессии.<br>Рассмотрим конкретный пример отыскания Sn. Дана конечная арифметическая прогрессия 1, 2, 3, ..., 98, 99, 100. Сумму ее членов вычислим следующим образом: | + | [[Image:Al91638.jpg]]<br>Аналогично можно установить, что [[Image:Al91639.jpg]] и вообще что сумма члена, находящегося на к-м месте от начала конечной арифметической прогрессии, и члена, находящегося на к-м месте от ее конца, равна сумме первого и последнего членов прогрессии.<br>Рассмотрим конкретный пример отыскания Sn. Дана конечная арифметическая прогрессия 1, 2, 3, ..., 98, 99, 100. Сумму ее членов вычислим следующим образом: |
| | | | |
| - | [[Image:al91640.jpg]]<br>'''Замечание.''' Рассказывают, что немецкий математик XIX века Карл Фридрих Гаусс додумался до приведенного выше решения примера в возрасте 5 лет.<br>Применим аналогичную идею для произвольной арифметической прогрессии. Имеем: | + | [[Image:Al91640.jpg]]<br>'''Замечание.''' Рассказывают, что немецкий математик XIX века Карл Фридрих Гаусс додумался до приведенного выше решения примера в возрасте 5 лет.<br>Применим аналогичную идею для произвольной арифметической прогрессии. Имеем: |
| | | | |
| - | [[Image:al91641.jpg]]<br>Сложив эти два равенства, получим | + | [[Image:Al91641.jpg]]<br>Сложив эти два равенства, получим |
| | | | |
| - | [[Image:al91642.jpg]]<br>В правой части равенства п пар слагаемых, каждая пара, как мы установили выше, равна а<sub>1</sub> + а<sub>n</sub>. Значит, получаем | + | [[Image:Al91642.jpg]]<br>В правой части равенства п пар слагаемых, каждая пара, как мы установили выше, равна а<sub>1</sub> + а<sub>n</sub>. Значит, получаем |
| | | | |
| - | [[Image:al91643.jpg]]<br>Это — формула суммы п членов арифметической прогрессии.<br>127<br>4.16. ||<br>ПРОГРЕССИИ<br>Пример 6. Дана конечная арифметическая прогрессия а . и . а.....а .<br>1' 2 3' ' п<br>а) Известно, что ах = 5, д, = 4, п = 22. Найти <§п, т.е. <§22.<br>б) Известно, что ах = 7, п = 8, 58 = 140. Найти й.<br>Р е ш е н и е. а) Имеем а = а, = а, + 21й = 5 + 21•4 = 89.<br>' Л 1<br>Значит, 522 = 22(а^) = 11 • (5 + 89) = 1034.<br>б) Сначала найдем ап, т.е. а8. Имеем<br>_ 8(а1 + а8) " ^ '<br>т.е.<br>140 = 4 (ах + а8), 140 = 4(7 + а8), 35 = 7 + а8.<br>В итоге получаем, что а8 = 28.<br>А теперь применим к а8 формулу п-го члена арифметической прогрессии а8 = а1 + 16,, т.е. 28 = 7 + Чй, откуда находим 6 = 3. О т в е т: а) 522= 1034; 6)6 = 3.<br>Пример 7. Найти сумму всех четных трехзначных чисел. Решение. Речь идет о сумме членов конечной арифметической прогрессии 100,102,104,..., 998. У этой прогрессии а1 = 100, ап = 998, 6 = 2. Нужно вычислить 8п, но для этого сначала надо узнать, чему равно п, т.е. сколько членов содержится в указанной конечной арифметической прогрессии. Имеем последовательно:<br>а= аг + (л - 1)6, 998 = 100 + (л - 1) • 2, 998 = 2п + 98, п = 450.<br>Итак, а1 = 100, п = 450, ап = 998. Наша задача — вычислить<br>5„> Т-е- 5460-<br>Имеем<br>2<br>Ответ: 247 050.<br>«450 = \ 460 = 225 (100 + 998) = 247050.<br>128<br>4.15.<br>ПРОГРЕССИИ<br>Иногда оказывается полезной несколько видоизмененная формула суммы п членов арифметической прогрессии. Если в формуле для <§п учесть, что ап = а1 + й(п - 1), то получим<br>2а, + Л(п - 1)<br>& = —4- • п.<br>2<br>Пример 8. Турист, двигаясь по сильно пересеченной местности, за первый час пути прошел 800 м, а за каждый следующий час проходил на 25 м меньше, чем за предыдущий. Сколько времени он потратил на весь путь, равный 5700 м?<br>Решение. Первый этап. Составление математической модели.<br>За первый час турист прошел 800 м, за второй — 775 м, за третий — 750 м и т.д. Математической моделью является конечная арифметическая прогрессия<br>+ а1> а2>аз> —>ап><br>у которой аг = 800, Л = -25, 5п = 5700. Надо найти п (в часах — время движения туриста).<br>Второй этап. Работа с составленной моделью. Воспользуемся второй формулой для<br>„ 2а, + Л(п - 1)<br>о = —-- • п,<br>2<br>т.е.<br>5700 = 2 8°°-25(п-1) • п, 2<br>228 = 64 -("-Ц .п 2<br>(обе части уравнения разделили на 25),<br>456 = л(65 - п), п2 -65л + 456 = 0, пх = 8, п2 = 57.<br>Третий этап. Ответ на вопрос задачи.<br>Спрашивается, сколько времени был в пути турист. По смыслу задачи из двух найденных значений п выбираем первое: п = 8. Ответ: турист был в пути 8 часов.<br>9-'6 129<br>4.16. ||<br>ПРОГРЕССИИ<br>4. Характеристическое свойство арифметической прогрессии.<br>Пусть дана арифметическая прогрессия а , а2, а3,..., ап,.... Рассмотрим три ее члена, следующие друг за другом: ап1, ап, ая+1. Известно, что<br>а -& = а .,<br>Л я—1<br>а + (1 = а ,.<br>п п+1<br>Сложив эти равенства, получим<br>а =<br>Это значит, что каждый член арифметической прогрессии (кроме первого и последнего)равен среднему арифметическому предшествующего и последующего членов.<br>Верно и обратное: если последовательность (ая) такова, что для любого п > 1 выполняется равенство<br>а , + а , а = ""<br>то (ап) — арифметическая прогрессия.<br>В самом деле, последнее равенство можно переписать в виде а -а = а - а .<br>п л-1 л+1 п<br>Это значит, в частности, что а2~ ах = а3 - а2, а3 - а2 = а4 - а3 и т.д. Иными словами, разность между любым членом последовательности и предшествующим ему всегда одна и та же, а это и означает, что задана арифметическая прогрессия.<br>Тем самым мы доказали следующую теорему.<br>Числовая последовательность является арифметической прогрессией тогда и только тогда, когда каждый ее член, кроме первого (и последне-Теорема го> в случае конечной последовательности),<br>равен среднему арифметическому предшествующего и последующего членов (характеристическое свойство арифметической прогрессии).<br>Пример 9. При каком значении х числа Зх + 2, Ьх - 4 и Их + 12 образуют конечную арифметическую прогрессию?<br>130<br>4.16.<br>ПРОГРЕССИИ<br>Решение. Согласно характеристическому свойству, заданные выражения должны удовлетворять соотношению<br>5х - 4 = <3*+ 2) + (Их + 12) 2<br>Решая это уравнение, находим:<br>10х - 8 = 14х +14, х = -5,5.<br>При этом значении х заданные выражения Зх + 2, 5х - 4, Их + 12 принимают соответственно значения -14,5, -31,5, -48,5. Это арифметическая прогрессия, ее разность равна -17. О т в е т: х = -5,5. | + | [[Image:Al91643.jpg]]<br>''Это — формула суммы п членов арифметической прогрессии.''<br>'''Пример 6.''' Дана конечная арифметическая прогрессия |
| | + | |
| | + | [[Image:al91644.jpg]]<br>'''Р е ш е н и е. а)''' Имеем |
| | + | |
| | + | [[Image:al91645.jpg]]<br>'''б)''' Сначала найдем |
| | + | |
| | + | [[Image:al91646.jpg]] |
| | + | |
| | + | В итоге получаем, что а<sub>8</sub> = 28.<br>А теперь применим к а<sub>8</sub> формулу п-го члена арифметической прогрессии а<sub>8</sub> = а1 + 16,, т.е. 28 = 7 + d, откуда находим d = 3. |
| | + | |
| | + | '''О т в е т: а) '''S<sub>22</sub>= 1034; '''б)''' d = 3.<br>'''Пример 7.''' Найти сумму всех четных трехзначных чисел. Решение. Речь идет о сумме членов конечной арифметической прогрессии 100,102,104,..., 998. У этой прогрессии а<sub>1</sub> = 100, а<sub>п</sub> = 998, d = 2. Нужно вычислить 8<sub>п</sub>, но для этого сначала надо узнать, чему равно п, т.е. сколько членов содержится в указанной конечной арифметической прогрессии. Имеем последовательно: |
| | + | |
| | + | [[Image:al91647.jpg]]<br>Итак, а<sub>1</sub> = 100, п = 450, а<sub>п</sub> = 998. Наша задача — вычислить<br>[[Image:al91648.jpg]]<br>Имеем<br>[[Image:al91649.jpg]]<br>'''Ответ:''' 247 050.<br>Иногда оказывается полезной несколько видоизмененная формула суммы п членов арифметической прогрессии. Если в формуле для Sn учесть, что аn = а<sub>1</sub> + d(п - 1), то получим |
| | + | |
| | + | [[Image:al91650.jpg]]<br>'''Пример 8.''' Турист, двигаясь по сильно пересеченной местности, за первый час пути прошел 800 м, а за каждый следующий час проходил на 25 м меньше, чем за предыдущий. Сколько времени он потратил на весь путь, равный 5700 м?<br>'''Решение. Первый этап. '''Составление математической модели.<br>За первый час турист прошел 800 м, за второй — 775 м, за третий — 750 м и т.д. Математической моделью является конечная арифметическая прогрессия [[Image:al91651.jpg]] |
| | + | |
| | + | у которой а<sub>1</sub> = 800, d = -25, Sn = 5700. Надо найти п (в часах — время движения туриста).<br>'''Второй этап.''' Работа с составленной моделью. Воспользуемся второй формулой для Sn |
| | + | |
| | + | [[Image:al91652.jpg]]<br>'''Третий этап.''' Ответ на вопрос задачи.<br>Спрашивается, сколько времени был в пути турист. По смыслу задачи из двух найденных значений п выбираем первое: п = 8. |
| | + | |
| | + | '''Ответ:''' турист был в пути 8 часов. |
| | + | |
| | + | <br>9-'6 129<br>4.16. ||<br>ПРОГРЕССИИ<br>4. Характеристическое свойство арифметической прогрессии.<br>Пусть дана арифметическая прогрессия а , а2, а3,..., ап,.... Рассмотрим три ее члена, следующие друг за другом: ап1, ап, ая+1. Известно, что<br>а -& = а .,<br>Л я—1<br>а + (1 = а ,.<br>п п+1<br>Сложив эти равенства, получим<br>а =<br>Это значит, что каждый член арифметической прогрессии (кроме первого и последнего)равен среднему арифметическому предшествующего и последующего членов.<br>Верно и обратное: если последовательность (ая) такова, что для любого п > 1 выполняется равенство<br>а , + а , а = ""<br>то (ап) — арифметическая прогрессия.<br>В самом деле, последнее равенство можно переписать в виде а -а = а - а .<br>п л-1 л+1 п<br>Это значит, в частности, что а2~ ах = а3 - а2, а3 - а2 = а4 - а3 и т.д. Иными словами, разность между любым членом последовательности и предшествующим ему всегда одна и та же, а это и означает, что задана арифметическая прогрессия.<br>Тем самым мы доказали следующую теорему.<br>Числовая последовательность является арифметической прогрессией тогда и только тогда, когда каждый ее член, кроме первого (и последне-Теорема го> в случае конечной последовательности),<br>равен среднему арифметическому предшествующего и последующего членов (характеристическое свойство арифметической прогрессии).<br>Пример 9. При каком значении х числа Зх + 2, Ьх - 4 и Их + 12 образуют конечную арифметическую прогрессию?<br>130<br>4.16.<br>ПРОГРЕССИИ<br>Решение. Согласно характеристическому свойству, заданные выражения должны удовлетворять соотношению<br>5х - 4 = <3*+ 2) + (Их + 12) 2<br>Решая это уравнение, находим:<br>10х - 8 = 14х +14, х = -5,5.<br>При этом значении х заданные выражения Зх + 2, 5х - 4, Их + 12 принимают соответственно значения -14,5, -31,5, -48,5. Это арифметическая прогрессия, ее разность равна -17. О т в е т: х = -5,5. |
| | | | |
| | А.Г. Мордкович Алгебра 9 класс | | А.Г. Мордкович Алгебра 9 класс |
Версия 10:43, 1 июля 2010
Гипермаркет знаний>>Математика>>Математика 9 класс>>Математика: Арифметическая прогрессия
АРИФМЕТИЧЕСКАЯ ПРОГРЕССИЯ
1. Основные понятия.
Определение. Числовую последовательность, каждый член которой, начиная со второго, равен сумме предыдущего члена и одного и того же числа d, называют арифметической прогрессией, а число d — разностью арифметической прогрессии.
Таким образом, арифметическая прогрессия — это числовая последовательность (аn), заданная рекуррентно соотношениями
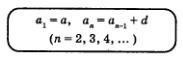
(а и д, — заданные числа).
Можно ли, глядя на числовую последовательность, определить, является ли она арифметической прогрессией? Можно. Если вы убедились в том, что разность между любым членом последовательности и предшествующим ему членом постоянна 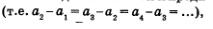 то перед вами — арифметическая прогрессия. Разумеется, при этом предполагается, что обнаруженная закономерность справедлива не только для явно выписанных членов последовательности, но и для всей последовательности в целом. то перед вами — арифметическая прогрессия. Разумеется, при этом предполагается, что обнаруженная закономерность справедлива не только для явно выписанных членов последовательности, но и для всей последовательности в целом.
Пример 1. 1, 3, 5, 7, 9,11,... .
Это арифметическая прогрессия, у которой а1 = 1, d = 2.
Пример 2. 20,17, 14, 11, 8, 5, 2, -1, -4, ... .
Это арифметическая прогрессия, у которой а1 = 20, d = -3.
Пример 3. 8, 8, 8, 8, 8, 8,... .
Это арифметическая прогрессия, у которой а1 = 8, d = 0.
Очевидно, что арифметическая прогрессия является возрастающей последовательностью, если d > 0 (см. пример 1), и убывающей, если d < 0 (см. пример 2).
Для обозначения того, что последовательность (аn) является арифметической прогрессией, иногда бывает удобна следующая запись:
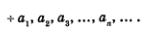
Значок + заменяет словосочетание «арифметическая прогрессия».
Если в арифметической прогрессии отбросить все члены, следующие за каким-то конкретным членом последовательности, например за аn, то получится конечная арифметическая прогрессия
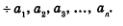
Иногда в конечной арифметической прогрессии удобно записывать не только несколько членов в начале, но и несколько членов в конце, например так:
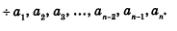
В дальнейших пунктах этого параграфа рассмотрим наиболее важные свойства арифметической прогрессии.
2. Формула п-го члена арифметической прогрессии.
Задание арифметической прогрессии, о котором идет речь в определении, является рекуррентным. Во многих случаях оно неудобно: чтобы вычислить, например, аш, надо предварительно найти предшествующие 99 членов последовательности. Эту вычислительную работу можно существенно упростить, если удастся найти формулу п-го члена, т.е. перейти к аналитическому заданию арифметической прогрессии.
Рассмотрим арифметическую прогрессию 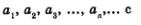 с разностью й. Имеем: с разностью й. Имеем:
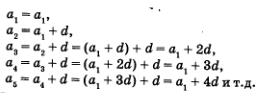
Нетрудно догадаться, что для любого номера п справедливо равенство
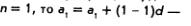
Это — формула п-го члена арифметической прогрессии.
Важное -замечание. «Нетрудно догадаться», «можно сообразить» и т.д. — это стилистические обороты из области интуиции, догадки, озарения. Разумеется, математики ими пользуются, но в основном для открытия каких-то новых фактов, а не для их обоснования. Формулу (1) мы «прочувствовали», но не обосновали. Приведем (для интересующихся) доказательство.
Если 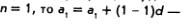 верное равенство, т.е. формула (1) для п = 1 верна. верное равенство, т.е. формула (1) для п = 1 верна.
Предположим, что формула (1) верна для натурального числа п — к, т.е. предположим, что верно равенство 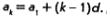 Докажем, что тогда формула (1) верна и для следующего натурального числа л = к+ 1, т.е. докажем, что Докажем, что тогда формула (1) верна и для следующего натурального числа л = к+ 1, т.е. докажем, что 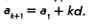
В самом деле, по определению арифметической прогрессии, 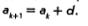 Далее имеем Далее имеем 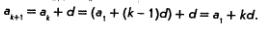
А теперь смотрите: для л = 1 формула (1) верна (это мы проверили). Далее мы доказали, что если формула (1) верна для л = к, то она верна и для п = к + 1. Воспользуемся этим: формула (1) верна для п — 1, значит, она верна и для п = 2; так как она верна для п — 2, то она верна и для п = 3 и т.д. Значит, формула (1) верна для любого натурального числа п.
Приведенный метод рассуждений носит название «метод математической индукции».
Перепишем формулу п-го члена арифметической прогрессии 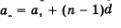 в виде в виде 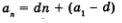 и введем обозначения: и введем обозначения: 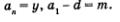 Получим у = dn + m, или, подробнее, Получим у = dn + m, или, подробнее,
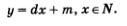
Значит, арифметическую прогрессию можно рассматривать как линейную функцию (у = dх + m), заданную на множестве N натуральных чисел. Угловой коэффициент этой линейной функции равен й — разности арифметической прогрессии. На рис. 95 схематически изображен график арифметической прогрессии — изолированные точки на прямой (с абсциссами х = 1, х = 2, х = 3 и т.д.).
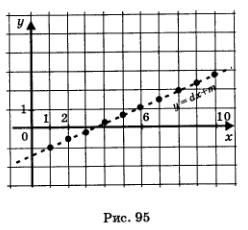
Вернемся к примерам 1, 2 и 3, рассмотренным выше. 1) 1, 3, 5, 7, 9, 11, ... . Это арифметическая прогрессия, у которой ах — 1, d = 2. Составим формулу п-го члена:
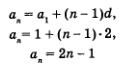
(заметим, что эту формулу нетрудно было угадать, глядя на заданную последовательность нечетных чисел 1, 3, 5, 7, ...).
2) 20, 17, 14, 11, 8, 5, 2, -1, -4, ... . Это арифметическая прогрессия, у которой а1 = 20, d = -3. Составим формулу п-го члена:
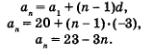
3) 8,8, 8.....Это арифметическая прогрессия, у которой а1 = 8, d = 0. Составим формулу п-го члена:
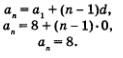
Пример 4. Дана арифметическая прогрессия
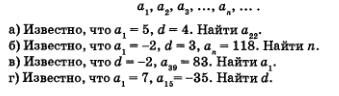
Решение. Во всех случаях в основе решения лежит формула п-го члена арифметической прогрессии
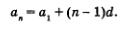
а) Положив в формуле п-го члена арифметической прогрессии п = 22,получим
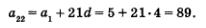
б) Имеем
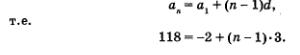
Решая составленное линейное уравнение, находим:
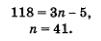
в) Имеем

Из этого уравнения находим а1 = 159.
г) Имеем

Из этого уравнения находим: 14d = -42, d = -3.
О т в е т: а) а22 = 89; б) п = 41; в) а1 = 159; г) d = -3.
Пример 5. При делении девятого члена арифметической прогрессии на второй ее член в частном получается 7; при делении десятого члена прогрессии на ее пятый член в частном получается 2 и в остатке 5. Найти двадцатый член этой прогрессии.
Решение. Первый этап. Составление математической модели.
Условия задачи можно кратко записать так:
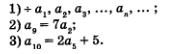
Воспользовавшись (несколько раз) формулой п-го члена арифметической прогрессии, получим:
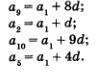
Тогда второе условие задачи (а9 = 7а2) можно записать в виде
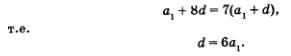
Третье условие задачи (а10= 2а5 + 5) можно записать в виде
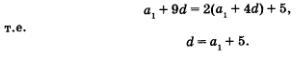
В итоге получаем очень простую систему двух линейных уравнений с двумя переменными а1 и d:
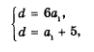
которая в сочетании с записанным выше условием 1) и представляет собой математическую модель задачи.
Второй этап. Работа с составленной моделью.
Решая систему, находим a1 = 1, d = 6.
Теперь мы можем записать арифметическую прогрессию 1,7, 13,19, 25,31,....
Третий этап. Ответ на вопрос задачи.
Требуется вычислить а20. Имеем 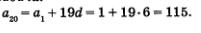
О т в е т: а20 = 115.
Замечание. В рассмотренном примере речь шла о конкретной математической модели — арифметической прогрессии. Первый этап решения мы назвали, как обычно, «составление математической модели». Получается, что мы составили математическую модель для математической модели. Как это понимать? Дело в том, что при решении задач очень часто приходится заменять одну математическую модель другой, более простой. Так обстоит дело и в рассмотренной задаче: математическую модель, оформленную в виде условий 1), 2) и 3), нам удалось заменить более привычной моделью — системой уравнений.
3. Формула суммы членов конечной арифметической прогрессии.
Пусть дана конечная арифметическая прогрессия
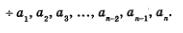
Обозначим через Sn сумму ее членов, т.е.
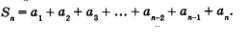
Выведем формулу для нахождения этой суммы.
Для начала заметим, что 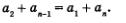
В самом деле, по определению арифметической прогрессии,
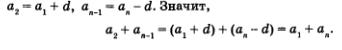
Аналогично можно установить, что 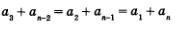 и вообще что сумма члена, находящегося на к-м месте от начала конечной арифметической прогрессии, и члена, находящегося на к-м месте от ее конца, равна сумме первого и последнего членов прогрессии. и вообще что сумма члена, находящегося на к-м месте от начала конечной арифметической прогрессии, и члена, находящегося на к-м месте от ее конца, равна сумме первого и последнего членов прогрессии.
Рассмотрим конкретный пример отыскания Sn. Дана конечная арифметическая прогрессия 1, 2, 3, ..., 98, 99, 100. Сумму ее членов вычислим следующим образом:
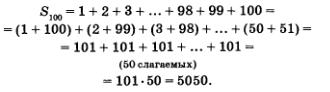
Замечание. Рассказывают, что немецкий математик XIX века Карл Фридрих Гаусс додумался до приведенного выше решения примера в возрасте 5 лет.
Применим аналогичную идею для произвольной арифметической прогрессии. Имеем:
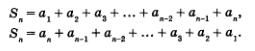
Сложив эти два равенства, получим
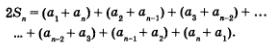
В правой части равенства п пар слагаемых, каждая пара, как мы установили выше, равна а1 + аn. Значит, получаем
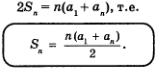
Это — формула суммы п членов арифметической прогрессии.
Пример 6. Дана конечная арифметическая прогрессия
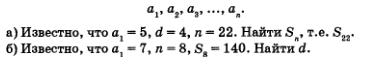
Р е ш е н и е. а) Имеем
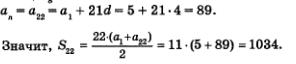
б) Сначала найдем
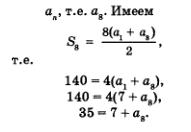
В итоге получаем, что а8 = 28.
А теперь применим к а8 формулу п-го члена арифметической прогрессии а8 = а1 + 16,, т.е. 28 = 7 + d, откуда находим d = 3.
О т в е т: а) S22= 1034; б) d = 3.
Пример 7. Найти сумму всех четных трехзначных чисел. Решение. Речь идет о сумме членов конечной арифметической прогрессии 100,102,104,..., 998. У этой прогрессии а1 = 100, ап = 998, d = 2. Нужно вычислить 8п, но для этого сначала надо узнать, чему равно п, т.е. сколько членов содержится в указанной конечной арифметической прогрессии. Имеем последовательно:
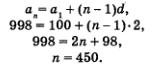
Итак, а1 = 100, п = 450, ап = 998. Наша задача — вычислить
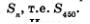
Имеем
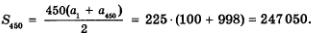
Ответ: 247 050.
Иногда оказывается полезной несколько видоизмененная формула суммы п членов арифметической прогрессии. Если в формуле для Sn учесть, что аn = а1 + d(п - 1), то получим
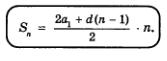
Пример 8. Турист, двигаясь по сильно пересеченной местности, за первый час пути прошел 800 м, а за каждый следующий час проходил на 25 м меньше, чем за предыдущий. Сколько времени он потратил на весь путь, равный 5700 м?
Решение. Первый этап. Составление математической модели.
За первый час турист прошел 800 м, за второй — 775 м, за третий — 750 м и т.д. Математической моделью является конечная арифметическая прогрессия Файл:Al91651.jpg
у которой а1 = 800, d = -25, Sn = 5700. Надо найти п (в часах — время движения туриста).
Второй этап. Работа с составленной моделью. Воспользуемся второй формулой для Sn

Третий этап. Ответ на вопрос задачи.
Спрашивается, сколько времени был в пути турист. По смыслу задачи из двух найденных значений п выбираем первое: п = 8.
Ответ: турист был в пути 8 часов.
9-'6 129
4.16. ||
ПРОГРЕССИИ
4. Характеристическое свойство арифметической прогрессии.
Пусть дана арифметическая прогрессия а , а2, а3,..., ап,.... Рассмотрим три ее члена, следующие друг за другом: ап1, ап, ая+1. Известно, что
а -& = а .,
Л я—1
а + (1 = а ,.
п п+1
Сложив эти равенства, получим
а =
Это значит, что каждый член арифметической прогрессии (кроме первого и последнего)равен среднему арифметическому предшествующего и последующего членов.
Верно и обратное: если последовательность (ая) такова, что для любого п > 1 выполняется равенство
а , + а , а = ""
то (ап) — арифметическая прогрессия.
В самом деле, последнее равенство можно переписать в виде а -а = а - а .
п л-1 л+1 п
Это значит, в частности, что а2~ ах = а3 - а2, а3 - а2 = а4 - а3 и т.д. Иными словами, разность между любым членом последовательности и предшествующим ему всегда одна и та же, а это и означает, что задана арифметическая прогрессия.
Тем самым мы доказали следующую теорему.
Числовая последовательность является арифметической прогрессией тогда и только тогда, когда каждый ее член, кроме первого (и последне-Теорема го> в случае конечной последовательности),
равен среднему арифметическому предшествующего и последующего членов (характеристическое свойство арифметической прогрессии).
Пример 9. При каком значении х числа Зх + 2, Ьх - 4 и Их + 12 образуют конечную арифметическую прогрессию?
130
4.16.
ПРОГРЕССИИ
Решение. Согласно характеристическому свойству, заданные выражения должны удовлетворять соотношению
5х - 4 = <3*+ 2) + (Их + 12) 2
Решая это уравнение, находим:
10х - 8 = 14х +14, х = -5,5.
При этом значении х заданные выражения Зх + 2, 5х - 4, Их + 12 принимают соответственно значения -14,5, -31,5, -48,5. Это арифметическая прогрессия, ее разность равна -17. О т в е т: х = -5,5.
А.Г. Мордкович Алгебра 9 класс
Материалы по математике онлайн, задачи и ответы по классам, планы конспектов уроков по математике скачать
Содержание урока
 конспект урока конспект урока
 опорный каркас опорный каркас
 презентация урока презентация урока
 акселеративные методы акселеративные методы
 интерактивные технологии
Практика интерактивные технологии
Практика
 задачи и упражнения задачи и упражнения
 самопроверка самопроверка
 практикумы, тренинги, кейсы, квесты практикумы, тренинги, кейсы, квесты
 домашние задания домашние задания
 дискуссионные вопросы дискуссионные вопросы
 риторические вопросы от учеников
Иллюстрации риторические вопросы от учеников
Иллюстрации
 аудио-, видеоклипы и мультимедиа аудио-, видеоклипы и мультимедиа
 фотографии, картинки фотографии, картинки
 графики, таблицы, схемы графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты
Дополнения притчи, поговорки, кроссворды, цитаты
Дополнения
 рефераты рефераты
 статьи статьи
 фишки для любознательных фишки для любознательных
 шпаргалки шпаргалки
 учебники основные и дополнительные учебники основные и дополнительные
 словарь терминов словарь терминов
 прочие
Совершенствование учебников и уроков прочие
Совершенствование учебников и уроков
 исправление ошибок в учебнике исправление ошибок в учебнике
 обновление фрагмента в учебнике обновление фрагмента в учебнике
 элементы новаторства на уроке элементы новаторства на уроке
 замена устаревших знаний новыми
Только для учителей замена устаревших знаний новыми
Только для учителей
 идеальные уроки идеальные уроки
 календарный план на год календарный план на год
 методические рекомендации методические рекомендации
 программы программы
 обсуждения
Интегрированные уроки обсуждения
Интегрированные уроки
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.
|