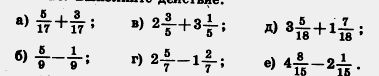|
|
|
| Строка 63: |
Строка 63: |
| | 123. Какие простые числа являются решениями неравенства 17<р<44? | | 123. Какие простые числа являются решениями неравенства 17<р<44? |
| | | | |
| - | 124. Могут ли быть простыми числами координаты точек А, Б, С и D (рис. 5), если р — простое число? | + | 124. Могут ли быть простыми числами координаты точек А, Б, С и D (рис. 5), если р — простое число? |
| | | | |
| - | [[Image:18-07-28.jpg]] <br><br>125. Представьте | + | [[Image:18-07-28.jpg]] <br><br>125. Представьте |
| | | | |
| | а) число 3 в виде дроби со знаменателем 5; | | а) число 3 в виде дроби со знаменателем 5; |
| | | | |
| - | б) число 1 со знаменателем 12. | + | б) число 1 со знаменателем 12. |
| | | | |
| - | 126. Выполните действие: | + | 126. Выполните действие: |
| | | | |
| - | [[Image:18-07-29.jpg]]<br><br>127. Из 35 учащихся пятого класса 22 выписывают журнал «Юный натуралист», 27 — газету «Пионерская правда», а 3 ученика не выписывают ни газету, ни журнал. Сколько учащихся выписывают газету и журнал? | + | [[Image:18-07-29.jpg]]<br><br>127. Из 35 учащихся пятого класса 22 выписывают журнал «Юный натуралист», 27 — газету «Пионерская правда», а 3 ученика не выписывают ни газету, ни журнал. Сколько учащихся выписывают газету и журнал? |
| | | | |
| - | 128. а) Книга на 100% дороже альбома. На сколько процентов альбом дешевле книги? | + | 128. а) Книга на 100% дороже альбома. На сколько процентов альбом дешевле книги? |
| | | | |
| - | б) Масса гуся на 25% больше массы утки. На сколько процентов масса утки меньше массы гуся? | + | б) Масса гуся на 25% больше массы утки. На сколько процентов масса утки меньше массы гуся? |
| | | | |
| - | 129. Для какого числового выражения составлена программа вычислений на микрокалькуляторе: | + | 129. Для какого числового выражения составлена программа вычислений на микрокалькуляторе: |
| | | | |
| | [[Image:18-07-30.jpg]]<br><br>130. Стороны треугольника 12 см, 17 см и х см. | | [[Image:18-07-30.jpg]]<br><br>130. Стороны треугольника 12 см, 17 см и х см. |
| | | | |
| - | а) Составьте выражение для вычисления периметра этого треугольника, | + | а) Составьте выражение для вычисления периметра этого треугольника, |
| | | | |
| | б) Подумайте, каким может быть значение х и каким быть не может. | | б) Подумайте, каким может быть значение х и каким быть не может. |
| | | | |
| - | 131. Решите задачу: | + | 131. Решите задачу: |
| | | | |
| - | 1) Две бригады хлопкоробов собрали вместе 20,4 ц хлопка за день. При атом первая бригада собрала на 1,52 ц больше второй. Сколько центнеров хлопка собрала каждая бригада?<br>2) Два комбайнера убрали пшеницу с 64,2 га. Сколько гектаров убрал каждый комбайнер, если первый убрал на 2,8 га меньше, чем второй? | + | 1) Две бригады хлопкоробов собрали вместе 20,4 ц хлопка за день. При атом первая бригада собрала на 1,52 ц больше второй. Сколько центнеров хлопка собрала каждая бригада?<br>2) Два комбайнера убрали пшеницу с 64,2 га. Сколько гектаров убрал каждый комбайнер, если первый убрал на 2,8 га меньше, чем второй? |
| | | | |
| - | 132. Найдите значение выражения: | + | 132. Найдите значение выражения: |
| | | | |
| - | 1) (13-9,5:3,8)• 0,3; 3) (1,3•2,8 + 1): 0,8;<br>2) (16,1:4,6-3,07)• 0,2; 4) (3,7•2,3-5):0,3. | + | 1) (13-9,5:3,8)• 0,3; 3) (1,3•2,8 + 1): 0,8;<br>2) (16,1:4,6-3,07)• 0,2; 4) (3,7•2,3-5):0,3. |
| | | | |
| - | m 183. На поверхности куба «¦¦ (рис. 6) найдите кратчайший путь:<br>а) из точки А в точку С через точку В;<br>б) из точки А в точку С, который пересекал бы все боковые ребра куба, кроме ребра АС.<br>®134. Разложите на простые множители числа: а> 54; 65; 99; 162; 10 000; б) 1500; 7000; 3240; 4608. 185. Выполните действия:<br>•> i+i-b « i-(i-T> -) -><br> Два тракториста вспахали 12,32 га земли, причем один из них вспахал в 1,2 раза меньше другого. Сколько гектаров земли вспахал каждый тракторист?<br> У покупателя было 22,3 р. В гастрономе он израсходовал в 6 раз меньше денег, чем в универмаге. Сколько денег израсходовал покупатель в универмаге, если у него осталось 1,3 р.?<br> Выполните действия:<br> <br>Рве. 6<br>а) (424,2 - 98,4): 3,6 • 0,9 + 9,1; б) (96,6+98,6): 6,4 • 1,2 - 0,2.<br><br><br><br><br><br>
| + | '''М''' 133. На поверхности куба (рис. 6) найдите кратчайший путь:<br>а) из точки А в точку С через точку В;<br>б) из точки А в точку С, который пересекал бы все боковые ребра куба, кроме ребра АС. |
| | + | |
| | + | [[Image:18-07-31.jpg]] |
| | + | |
| | + | <br>'''Д''' 134. Разложите на простые множители числа: |
| | + | |
| | + | а) 54; 65; 99; 162; 10 000; |
| | + | |
| | + | б) 1500; 7000; 3240; 4608. 185. |
| | + | |
| | + | 135.Выполните действия: |
| | + | |
| | + | [[Image:18-07-32.jpg]]<br><br>136. Два тракториста вспахали 12,32 га земли, причем один из них вспахал в 1,2 раза меньше другого. Сколько гектаров земли вспахал каждый тракторист? |
| | + | |
| | + | 137.У покупателя было 22,3 р. В гастрономе он израсходовал в 6 раз меньше денег, чем в универмаге. Сколько денег израсходовал покупатель в универмаге, если у него осталось 1,3 р.? |
| | + | |
| | + | 138. Выполните действия: |
| | + | |
| | + | а) (424,2 - 98,4): 3,6 • 0,9 + 9,1; |
| | + | |
| | + | б) (96,6+98,6): 6,4 • 1,2 - 0,2.<br><br><br><br><br><br> |
| | | | |
| | <br> ''Н.Я.Виленкин, А.С. Чесноков, С.И. Шварцбурд, В.И.Жохов, Математика для 6 класса, Учебник для средней школы'' <br> | | <br> ''Н.Я.Виленкин, А.С. Чесноков, С.И. Шварцбурд, В.И.Жохов, Математика для 6 класса, Учебник для средней школы'' <br> |
Версия 13:01, 19 июля 2010
Гипермаркет знаний>>Математика>>Математика 6 класс>>Математика:Разложение на простые множители
5. Разложение на простые множители
Число 210 является произведением чисел 21 и 10. Значит, 210=21.10. Числа 21 и 10 составные. Их тоже можно представить в виде произведения: 21 = 3.7, 10=2.7•2•5 все множители — простые числа. Таким образом, число 210 разложено
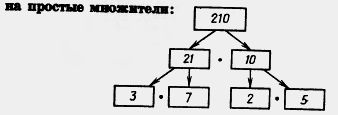
Число 210 можно разложить на простые множители иным способом: 210 = 30•7 = 10•3•7 = 5•2•3•7. Получились те же самые простые множители, только записанные в другом порядке. Обычно записывают множители в порядке их возрастания: 210=2•3•5•7.
Всякое составное число можно разложить на простые множители. При любом способе получается одно и то же разложение, если не учитывать порядка записи множителей.
При разложении чисел на простые множители используют признаки делимости.
Разложим, например, на простые множители число 756. Оно делится на 2, так как оканчивается четной цифрой 6. Имеем 756:2=378. Проведем вертикальную черту и запишем слева от нее делимое 756, а справа делитель 2. Частное запишем под числом 756.
Число 378 тоже делится на 2. При делении получаем в частном 189.

189 не делится на 2, так как оканчивается нечетной цифрой. Но 189 делится на 3, так как сумма его цифр (1+8+9=18) делится на 3. Имеем 189:3=63.
Число 63 также делится на 3. При делении получим число 21.
Число 21 также делим на 3, причем получаем в частном простое число 7.
При делении числа 7 на 7 получаем 1. Разложение на множители закончено. Значит, 756=2•2•3•3•3•7.
? Существуют ли составные числа, которые нельзя разло- жить на простые множители? Чем могут отличаться два разложения одного и того же числа на простые множители?
К 115. Разложите на простые множители числа:
а) 216; 162; 144; 512; 675; 1024;
б) 60; 180; 220; 350; 400; 1200; 8000;
в) 11; 1001; 1225; 21780; 45 630.
116. Напишите все двузначные числа, разложение которых на простые множители состоит:
а) из двух одинаковых множителей;
б) из трех одинаковых множителей.
117. Запишите все двузначные числа, которые раскладываются на два различных простых множителя, один из которых равен:
а) 11; б) 13; в) 23; г) 47.
118. Выясните, делится ли число а на число b без остатка, если:
а) а = 2•2•2•3•5•7 и b = 2•3•7;
б) а = 3•3•5•5•11 и b = 3• 3 5;
в) а = 3•3•5•7•13 и b = 3•5•5•13;
г) а = 2•3 •3 •7 •7 и b = 21;
д) а = 2•2•3•3•3•5•7 и b = 135;
е) а=2•2•2•3•3•5•5•5 и b = 1000.
в случае, когда а делится на b найдите частное.
П 119. Вычислите устно:
а) 3,99 + 2,01; 2,3 + 0,007; 3,62 + 1,08; 3,06 + 1,94; 12,77 + 0,13;
б) 0,7-0,06; 1- 0,48; 2-1,02; 0,65 - 0,5; 0,8-0,25;
в) 1,6:100; 5:10; 12:1000; 2,3:0,1; 4:0,01;
г) 0,4 0,31-25; 3,8-1,7-2,8-1,7; 4,7-12,5-0,8; 3,1 • 3,7 + 3,1 - 6,3; 49,3 + 0 49,3.
120. При каких натуральных значениях а произведение 23а является простым числом?
121. Существует ли прямоугольник, стороны которого выражаются натуральными числами, а периметр — простым числом?
122. Найдите по два простых делителя каждого из чисел: 64; 62; 148; 182; 3333; 5005.
123. Какие простые числа являются решениями неравенства 17<р<44?
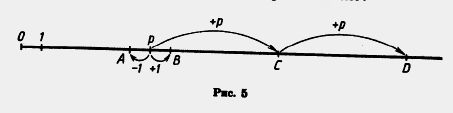
124. Могут ли быть простыми числами координаты точек А, Б, С и D (рис. 5), если р — простое число?
125. Представьте
а) число 3 в виде дроби со знаменателем 5;
б) число 1 со знаменателем 12.
126. Выполните действие:
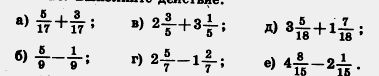
127. Из 35 учащихся пятого класса 22 выписывают журнал «Юный натуралист», 27 — газету «Пионерская правда», а 3 ученика не выписывают ни газету, ни журнал. Сколько учащихся выписывают газету и журнал?
128. а) Книга на 100% дороже альбома. На сколько процентов альбом дешевле книги?
б) Масса гуся на 25% больше массы утки. На сколько процентов масса утки меньше массы гуся?
129. Для какого числового выражения составлена программа вычислений на микрокалькуляторе:
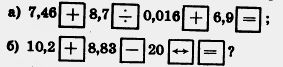
130. Стороны треугольника 12 см, 17 см и х см.
а) Составьте выражение для вычисления периметра этого треугольника,
б) Подумайте, каким может быть значение х и каким быть не может.
131. Решите задачу:
1) Две бригады хлопкоробов собрали вместе 20,4 ц хлопка за день. При атом первая бригада собрала на 1,52 ц больше второй. Сколько центнеров хлопка собрала каждая бригада?
2) Два комбайнера убрали пшеницу с 64,2 га. Сколько гектаров убрал каждый комбайнер, если первый убрал на 2,8 га меньше, чем второй?
132. Найдите значение выражения:
1) (13-9,5:3,8)• 0,3; 3) (1,3•2,8 + 1): 0,8;
2) (16,1:4,6-3,07)• 0,2; 4) (3,7•2,3-5):0,3.
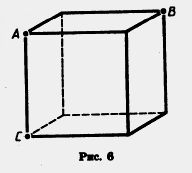
М 133. На поверхности куба (рис. 6) найдите кратчайший путь:
а) из точки А в точку С через точку В;
б) из точки А в точку С, который пересекал бы все боковые ребра куба, кроме ребра АС.
Д 134. Разложите на простые множители числа:
а) 54; 65; 99; 162; 10 000;
б) 1500; 7000; 3240; 4608. 185.
135.Выполните действия:
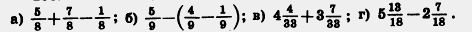
136. Два тракториста вспахали 12,32 га земли, причем один из них вспахал в 1,2 раза меньше другого. Сколько гектаров земли вспахал каждый тракторист?
137.У покупателя было 22,3 р. В гастрономе он израсходовал в 6 раз меньше денег, чем в универмаге. Сколько денег израсходовал покупатель в универмаге, если у него осталось 1,3 р.?
138. Выполните действия:
а) (424,2 - 98,4): 3,6 • 0,9 + 9,1;
б) (96,6+98,6): 6,4 • 1,2 - 0,2.
Н.Я.Виленкин, А.С. Чесноков, С.И. Шварцбурд, В.И.Жохов, Математика для 6 класса, Учебник для средней школы
Книги, учебники математике скачать, конспект на помощь учителю и ученикам, учиться онлайн
Содержание урока
 конспект урока конспект урока
 опорный каркас опорный каркас
 презентация урока презентация урока
 акселеративные методы акселеративные методы
 интерактивные технологии
Практика интерактивные технологии
Практика
 задачи и упражнения задачи и упражнения
 самопроверка самопроверка
 практикумы, тренинги, кейсы, квесты практикумы, тренинги, кейсы, квесты
 домашние задания домашние задания
 дискуссионные вопросы дискуссионные вопросы
 риторические вопросы от учеников
Иллюстрации риторические вопросы от учеников
Иллюстрации
 аудио-, видеоклипы и мультимедиа аудио-, видеоклипы и мультимедиа
 фотографии, картинки фотографии, картинки
 графики, таблицы, схемы графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты
Дополнения притчи, поговорки, кроссворды, цитаты
Дополнения
 рефераты рефераты
 статьи статьи
 фишки для любознательных фишки для любознательных
 шпаргалки шпаргалки
 учебники основные и дополнительные учебники основные и дополнительные
 словарь терминов словарь терминов
 прочие
Совершенствование учебников и уроков прочие
Совершенствование учебников и уроков
 исправление ошибок в учебнике исправление ошибок в учебнике
 обновление фрагмента в учебнике обновление фрагмента в учебнике
 элементы новаторства на уроке элементы новаторства на уроке
 замена устаревших знаний новыми
Только для учителей замена устаревших знаний новыми
Только для учителей
 идеальные уроки идеальные уроки
 календарный план на год календарный план на год
 методические рекомендации методические рекомендации
 программы программы
 обсуждения
Интегрированные уроки обсуждения
Интегрированные уроки
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.
|