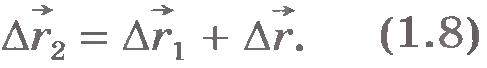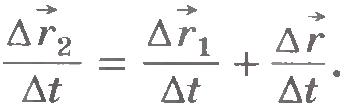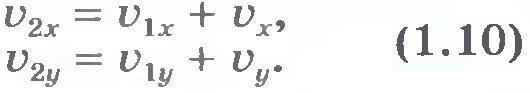|
|
|
| Строка 1: |
Строка 1: |
| | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Физика и астрономия|Физика и астрономия]]>>[[Физика 10 класс|Физика 10 класс]]>>Физика: Сложение скоростей ''' | | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Физика и астрономия|Физика и астрономия]]>>[[Физика 10 класс|Физика 10 класс]]>>Физика: Сложение скоростей ''' |
| | | | |
| | + | <br> |
| | | | |
| | + | <metakeywords>Физика, 10 класс, Сложение скоростей</metakeywords> |
| | | | |
| - | <metakeywords>Физика, 10 класс, Сложение скоростей</metakeywords> | + | Пусть по реке плывет моторная лодка и нам известна ее скорость [[Image:a10-5.jpg]], относительно воды, точнее, относительно системы отсчета ''К<sub>1</sub>'', движущейся вместе с водой.<br> Такую систему отсчета можно связать, например, с мячом, выпавшим из лодки и плывущим по течению. Если известна еще и скорость течения реки [[Image:a10-6.jpg]] относительно системы отсчета ''К<sub>2</sub>'', связанной с берегом, т. е. скорость системы отсчета''К<sub>1</sub>'' относительно системы отсчета ''К<sub>2</sub>'', то можно определить скорость лодки [[Image:a10-7.jpg]] относительно берега (''рис.1.20''). |
| | | | |
| | + | [[Image:a1.20.jpg|center]] За промежуток времени [[Image:a10-8.jpg]] перемещения лодки и мяча относительно берега равны [[Image:a10-9.jpg]] и [[Image:a10-10.jpg]] (''рис.1.20''), а перемещение лодки относительно мяча равно [[Image:a10-11.jpg]]. Из рисунка 1.21 видно, что <br> |
| | | | |
| | + | [[Image:a10-1.jpg|center]][[Image:a1.21.jpg|center]] Разделив левую и правую части уравнения (1.8) на [[Image:a10-8.jpg]], получим<br>[[Image:a10-2.jpg|center]] Учтем также, что отношения перемещений к интервалу времени равны скоростям. Поэтому<br>[[Image:a10-3.jpg|center]] Скорости складываются геометрически, как и все другие векторы.<br> Мы получили простой и замечательный результат, который называется законом сложения скоростей: '''если тело движется относительно некоторой системы отсчета ''К<sub>1</sub>'' со скоростью [[Image:a10-5.jpg]] и сама система отсчета''К<sub>1</sub> ''движется относительно другой системы отсчета ''К<sub>2</sub> ''со скоростью [[Image:a10-7.jpg]], то скорость тела относительно второй системы отсчета равна геометрической сумме скоростей [[Image:a10-5.jpg]] и [[Image:a10-6.jpg]].''' Закон сложения скоростей справедлив и для неравномерного движения. В этом случае складываются мгновенные скорости.<br> Как и любое векторное уравнение, уравнение (1.9) представляет собой компактную запись скалярных уравнений, в данном случае - для сложения проекций скоростей движения на плоскости:<br>[[Image:a10-4.jpg|center]] Проекции скоростей складываются алгебраически.<br> Закон сложения скоростей позволяет определять скорость тела относительно разных систем отсчета, движущихся относительно друг друга.<br> |
| | + | <br> |
| | | | |
| - | ''Г.Я.Мякишев, Б.Б.Буховцев, Н.Н.Сотский, Физика 10 класс'' | + | ''Г.Я.Мякишев, Б.Б.Буховцев, Н.Н.Сотский, Физика 10 класс'' |
| | | | |
| - | <br> <sub>Скачать календарно-тематическое планирование [[Физика_и_астрономия|по физике]], ответы на тесты, задания и ответы школьнику, [[Гипермаркет_знаний_-_первый_в_мире!|книги и учебники]], курсы учителю [[Физика_10_класс|по физике для 10 класса]]</sub> | + | <br> <sub>Скачать календарно-тематическое планирование [[Физика и астрономия|по физике]], ответы на тесты, задания и ответы школьнику, [[Гипермаркет знаний - первый в мире!|книги и учебники]], курсы учителю [[Физика 10 класс|по физике для 10 класса]]</sub> |
| | | | |
| | '''<u>Содержание урока</u>''' | | '''<u>Содержание урока</u>''' |
Версия 21:22, 2 августа 2010
Гипермаркет знаний>>Физика и астрономия>>Физика 10 класс>>Физика: Сложение скоростей
Пусть по реке плывет моторная лодка и нам известна ее скорость 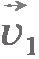 , относительно воды, точнее, относительно системы отсчета К1, движущейся вместе с водой. , относительно воды, точнее, относительно системы отсчета К1, движущейся вместе с водой.
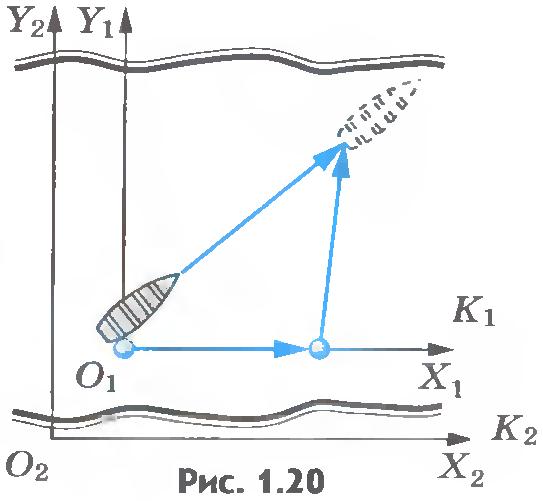
Такую систему отсчета можно связать, например, с мячом, выпавшим из лодки и плывущим по течению. Если известна еще и скорость течения реки 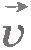 относительно системы отсчета К2, связанной с берегом, т. е. скорость системы отсчетаК1 относительно системы отсчета К2, то можно определить скорость лодки относительно системы отсчета К2, связанной с берегом, т. е. скорость системы отсчетаК1 относительно системы отсчета К2, то можно определить скорость лодки 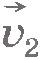 относительно берега (рис.1.20). относительно берега (рис.1.20).
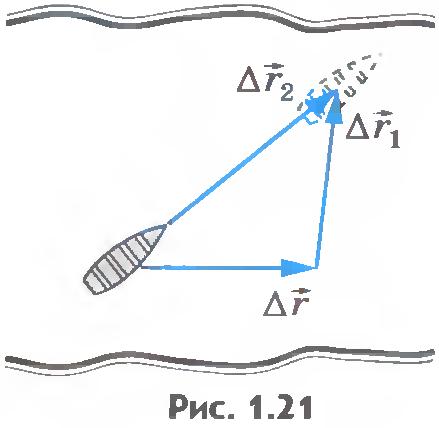
За промежуток времени  перемещения лодки и мяча относительно берега равны перемещения лодки и мяча относительно берега равны 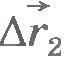 и и  (рис.1.20), а перемещение лодки относительно мяча равно (рис.1.20), а перемещение лодки относительно мяча равно 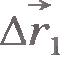 . Из рисунка 1.21 видно, что . Из рисунка 1.21 видно, что
Разделив левую и правую части уравнения (1.8) на  , получим , получим
Учтем также, что отношения перемещений к интервалу времени равны скоростям. Поэтому
Скорости складываются геометрически, как и все другие векторы.
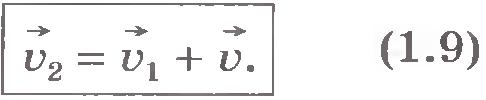
Мы получили простой и замечательный результат, который называется законом сложения скоростей: если тело движется относительно некоторой системы отсчета К1 со скоростью 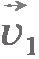 и сама система отсчетаК1 движется относительно другой системы отсчета К2 со скоростью и сама система отсчетаК1 движется относительно другой системы отсчета К2 со скоростью 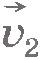 , то скорость тела относительно второй системы отсчета равна геометрической сумме скоростей , то скорость тела относительно второй системы отсчета равна геометрической сумме скоростей 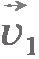 и и 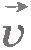 . Закон сложения скоростей справедлив и для неравномерного движения. В этом случае складываются мгновенные скорости. . Закон сложения скоростей справедлив и для неравномерного движения. В этом случае складываются мгновенные скорости.
Как и любое векторное уравнение, уравнение (1.9) представляет собой компактную запись скалярных уравнений, в данном случае - для сложения проекций скоростей движения на плоскости:
Проекции скоростей складываются алгебраически.
Закон сложения скоростей позволяет определять скорость тела относительно разных систем отсчета, движущихся относительно друг друга.
Г.Я.Мякишев, Б.Б.Буховцев, Н.Н.Сотский, Физика 10 класс
Скачать календарно-тематическое планирование по физике, ответы на тесты, задания и ответы школьнику, книги и учебники, курсы учителю по физике для 10 класса
Содержание урока
 конспект урока конспект урока
 опорный каркас опорный каркас
 презентация урока презентация урока
 акселеративные методы акселеративные методы
 интерактивные технологии
Практика интерактивные технологии
Практика
 задачи и упражнения задачи и упражнения
 самопроверка самопроверка
 практикумы, тренинги, кейсы, квесты практикумы, тренинги, кейсы, квесты
 домашние задания домашние задания
 дискуссионные вопросы дискуссионные вопросы
 риторические вопросы от учеников
Иллюстрации риторические вопросы от учеников
Иллюстрации
 аудио-, видеоклипы и мультимедиа аудио-, видеоклипы и мультимедиа
 фотографии, картинки фотографии, картинки
 графики, таблицы, схемы графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты
Дополнения притчи, поговорки, кроссворды, цитаты
Дополнения
 рефераты рефераты
 статьи статьи
 фишки для любознательных фишки для любознательных
 шпаргалки шпаргалки
 учебники основные и дополнительные учебники основные и дополнительные
 словарь терминов словарь терминов
 прочие
Совершенствование учебников и уроков прочие
Совершенствование учебников и уроков
 исправление ошибок в учебнике исправление ошибок в учебнике
 обновление фрагмента в учебнике обновление фрагмента в учебнике
 элементы новаторства на уроке элементы новаторства на уроке
 замена устаревших знаний новыми
Только для учителей замена устаревших знаний новыми
Только для учителей
 идеальные уроки идеальные уроки
 календарный план на год календарный план на год
 методические рекомендации методические рекомендации
 программы программы
 обсуждения
Интегрированные уроки обсуждения
Интегрированные уроки
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.
|
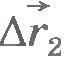 и
и 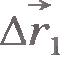 . Из рисунка 1.21 видно, что
. Из рисунка 1.21 видно, что