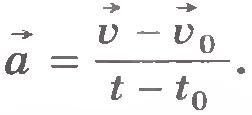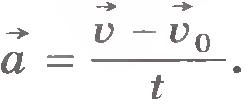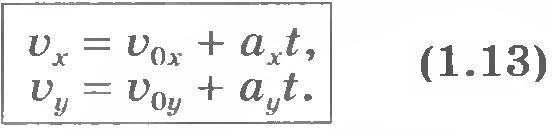|
|
|
| Строка 5: |
Строка 5: |
| | <metakeywords>Физика, 10 класс, Скорость при движении, с постоянным ускорением</metakeywords> | | <metakeywords>Физика, 10 класс, Скорость при движении, с постоянным ускорением</metakeywords> |
| | | | |
| - | Выясним зависимости скорости точки от времени при ее движении с постоянным ускорением. Для этого воспользуемся формулой<br>[[Image:a13-1.jpg|center]] Пусть [[Image:a13-7.jpg]] - скорость точки в начальный момент времени [[Image:a13-8.jpg]], а [[Image:a13-9.jpg]] - ее скорость в некоторый момент времени ''t''. Тогда [[Image:a13-10.jpg]][[Image:a13-11.jpg]], и формула для ускорения примет вид:<br>[[Image:a13-2.jpg|center]] Если начальный момент времени [[Image:a13-8.jpg]] принять равным нулю, то получим<br>[[Image:a13-3.jpg|center]]Отсюда<br>[[Image:a13-4.jpg|center]] Векторному уравнению (1.12) соответствуют в случае движения на плоскости два скалярных уравнения для проекций скорости на координатные оси ''X'' и ''Y'':<br>[[Image:a13-5.jpg|center]] Как видим, при движении с постоянным ускорением скорость со временем меняется по линейному закону.<br> Итак, для определения скорости в произвольный момент времени надо знать начальную скорость [[Image:a13-7.jpg]] и ускорение [[Image:a13-12.jpg]]. Начальную скорость нужно измерить. Ускорение, как мы увидим в дальнейшем, определяется действием на данное тело других тел и может быть вычислено. Начальная скорость зависит не от того, как действуют на данное тело другие тела в рассматриваемый момент времени, а от того, что происходило с телом в предшествующие моменты времени. Например, начальная скорость падающего камня зависит от того, выпустили его из рук или же бросили, совершив некоторое усилие.<br> Ускорение же, наоборот, не зависит от того, что происходило с телом в предыдущие моменты, а зависит лишь от действия на него других тел в данный момент времени.<br> Зависимость проекции скорости от времени можно изобразить наглядно с помощью графика.<br> Если начальная скорость равна нулю, то график зависимости проекции скорости на ось ''X'' от времени имеет вид прямой, выходящей из начала координат. На рисунке 1.29 представлен этот график в виде прямой ''1'' для случая [[Image:a13-13.jpg]]. По этому графику можно найти проекцию ускорения на ось ''X'':<br>[[Image:a13-6.jpg|center]][[Image:a1.29.jpg|center]]Чем больше [[Image:a13-14.jpg]], тем больший угол [[Image:a13-15.jpg]] с осью времени составляет график проекции скорости. Такая зависимость скорости от времени наблюдается при падении тела, покоившегося в начальный момент времени, с некоторой высоты или при движении автомобиля, трогающегося с места.<br> Если начальная скорость отлична от нуля и тело движется с большим ускорением, то график зависимости проекции скорости от времени имеет вид прямой ''2'' (см. ''рис.1.29'').<br> В случае отрицательного ускорения (равнозамедленное движение) с той же начальной скоростью график зависимости [[Image:a13-16.jpg]] от времени имеет вид прямой ''3''. Обратим внимание на то, что так как углы [[Image:a13-17.jpg]] и [[Image:a13-18.jpg]] по модулю равны, то равны по модулю проекции ускорения: [[Image:a13-19.jpg]].<br> Мы научились, таким образом, находить скорость материальной точки при движении с постоянным ускорением. | + | Выясним зависимости скорости точки от времени при ее движении с постоянным ускорением. Для этого воспользуемся формулой<br>[[Image:A13-1.jpg|center|78x44px]] Пусть [[Image:A13-7.jpg|20x27px]] - скорость точки в начальный момент времени [[Image:A13-8.jpg|20x20px]], а [[Image:A13-9.jpg|13x22px]] - ее скорость в некоторый момент времени ''t''. Тогда [[Image:A13-10.jpg|103x20px]], [[Image:A13-11.jpg|100x25px]], и формула для ускорения примет вид:<br>[[Image:A13-2.jpg|center|119x54px]] Если начальный момент времени [[Image:A13-8.jpg|19x20px]] принять равным нулю, то получим<br>[[Image:A13-3.jpg|center|123x51px]]Отсюда<br>[[Image:A13-4.jpg|center|237x48px]] Векторному уравнению (1.12) соответствуют в случае движения на плоскости два скалярных уравнения для проекций скорости на координатные оси ''X'' и ''Y'':<br>[[Image:A13-5.jpg|center|252x59px]] Как видим, при движении с постоянным ускорением скорость со временем меняется по линейному закону.<br> Итак, для определения скорости в произвольный момент времени надо знать начальную скорость [[Image:A13-7.jpg|21x27px]] и ускорение [[Image:A13-12.jpg|15x27px]]. Начальную скорость нужно измерить. Ускорение, как мы увидим в дальнейшем, определяется действием на данное тело других тел и может быть вычислено. Начальная скорость зависит не от того, как действуют на данное тело другие тела в рассматриваемый момент времени, а от того, что происходило с телом в предшествующие моменты времени. Например, начальная скорость падающего камня зависит от того, выпустили его из рук или же бросили, совершив некоторое усилие.<br> Ускорение же, наоборот, не зависит от того, что происходило с телом в предыдущие моменты, а зависит лишь от действия на него других тел в данный момент времени.<br> Зависимость проекции скорости от времени можно изобразить наглядно с помощью графика.<br> Если начальная скорость равна нулю, то график зависимости проекции скорости на ось ''X'' от времени имеет вид прямой, выходящей из начала координат. На рисунке 1.29 представлен этот график в виде прямой ''1'' для случая [[Image:A13-13.jpg|53x18px]]. По этому графику можно найти проекцию ускорения на ось ''X'':<br>[[Image:A13-6.jpg|center|308x40px]][[Image:A1.29.jpg|center|218x207px]]Чем больше [[Image:A13-14.jpg|25x20px]], тем больший угол [[Image:A13-15.jpg|18x16px]] с осью времени составляет график проекции скорости. Такая зависимость скорости от времени наблюдается при падении тела, покоившегося в начальный момент времени, с некоторой высоты или при движении автомобиля, трогающегося с места.<br> Если начальная скорость отлична от нуля и тело движется с большим ускорением, то график зависимости проекции скорости от времени имеет вид прямой ''2'' (см. ''рис.1.29'').<br> В случае отрицательного ускорения (равнозамедленное движение) с той же начальной скоростью график зависимости [[Image:A13-16.jpg|20x17px]] от времени имеет вид прямой ''3''. Обратим внимание на то, что так как углы [[Image:A13-17.jpg|24x18px]] и [[Image:A13-18.jpg|25x18px]] по модулю равны, то равны по модулю проекции ускорения: [[Image:A13-19.jpg|112x23px]].<br> Мы научились, таким образом, находить скорость материальной точки при движении с постоянным ускорением. |
| | | | |
| - | | + | <br> ''Г.Я.Мякишев, Б.Б.Буховцев, Н.Н.Сотский, Физика 10 класс'' |
| - | ''Г.Я.Мякишев, Б.Б.Буховцев, Н.Н.Сотский, Физика 10 класс'' | + | |
| | | | |
| | <br> <sub>Планирование уроков [[Физика и астрономия|по физике]], ответы на тесты, задания и ответы по классам, домашнее задание и работа [[Физика 10 класс|по физике для 10 класса]]</sub> | | <br> <sub>Планирование уроков [[Физика и астрономия|по физике]], ответы на тесты, задания и ответы по классам, домашнее задание и работа [[Физика 10 класс|по физике для 10 класса]]</sub> |
Версия 17:44, 3 августа 2010
Гипермаркет знаний>>Физика и астрономия>>Физика 10 класс>>Физика: Скорость при движении с постоянным ускорением
Выясним зависимости скорости точки от времени при ее движении с постоянным ускорением. Для этого воспользуемся формулой
Пусть 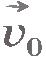 - скорость точки в начальный момент времени - скорость точки в начальный момент времени 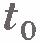 , а , а 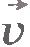 - ее скорость в некоторый момент времени t. Тогда - ее скорость в некоторый момент времени t. Тогда 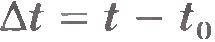 , , 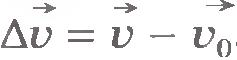 , и формула для ускорения примет вид: , и формула для ускорения примет вид:
Если начальный момент времени  принять равным нулю, то получим принять равным нулю, то получим
Отсюда
Векторному уравнению (1.12) соответствуют в случае движения на плоскости два скалярных уравнения для проекций скорости на координатные оси X и Y:
Как видим, при движении с постоянным ускорением скорость со временем меняется по линейному закону.
Итак, для определения скорости в произвольный момент времени надо знать начальную скорость 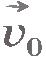 и ускорение и ускорение 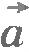 . Начальную скорость нужно измерить. Ускорение, как мы увидим в дальнейшем, определяется действием на данное тело других тел и может быть вычислено. Начальная скорость зависит не от того, как действуют на данное тело другие тела в рассматриваемый момент времени, а от того, что происходило с телом в предшествующие моменты времени. Например, начальная скорость падающего камня зависит от того, выпустили его из рук или же бросили, совершив некоторое усилие. . Начальную скорость нужно измерить. Ускорение, как мы увидим в дальнейшем, определяется действием на данное тело других тел и может быть вычислено. Начальная скорость зависит не от того, как действуют на данное тело другие тела в рассматриваемый момент времени, а от того, что происходило с телом в предшествующие моменты времени. Например, начальная скорость падающего камня зависит от того, выпустили его из рук или же бросили, совершив некоторое усилие.
Ускорение же, наоборот, не зависит от того, что происходило с телом в предыдущие моменты, а зависит лишь от действия на него других тел в данный момент времени.
Зависимость проекции скорости от времени можно изобразить наглядно с помощью графика.
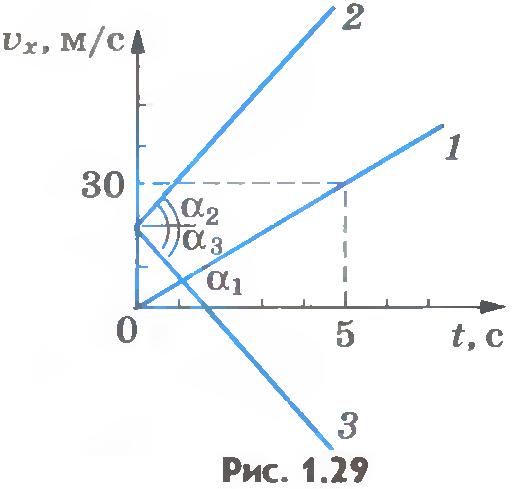
Если начальная скорость равна нулю, то график зависимости проекции скорости на ось X от времени имеет вид прямой, выходящей из начала координат. На рисунке 1.29 представлен этот график в виде прямой 1 для случая 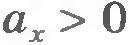 . По этому графику можно найти проекцию ускорения на ось X: . По этому графику можно найти проекцию ускорения на ось X:
Чем больше  , тем больший угол , тем больший угол 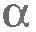 с осью времени составляет график проекции скорости. Такая зависимость скорости от времени наблюдается при падении тела, покоившегося в начальный момент времени, с некоторой высоты или при движении автомобиля, трогающегося с места. с осью времени составляет график проекции скорости. Такая зависимость скорости от времени наблюдается при падении тела, покоившегося в начальный момент времени, с некоторой высоты или при движении автомобиля, трогающегося с места.
Если начальная скорость отлична от нуля и тело движется с большим ускорением, то график зависимости проекции скорости от времени имеет вид прямой 2 (см. рис.1.29).
В случае отрицательного ускорения (равнозамедленное движение) с той же начальной скоростью график зависимости 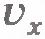 от времени имеет вид прямой 3. Обратим внимание на то, что так как углы от времени имеет вид прямой 3. Обратим внимание на то, что так как углы 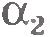 и и 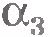 по модулю равны, то равны по модулю проекции ускорения: по модулю равны, то равны по модулю проекции ускорения:  . .
Мы научились, таким образом, находить скорость материальной точки при движении с постоянным ускорением.
Г.Я.Мякишев, Б.Б.Буховцев, Н.Н.Сотский, Физика 10 класс
Планирование уроков по физике, ответы на тесты, задания и ответы по классам, домашнее задание и работа по физике для 10 класса
Содержание урока
 конспект урока конспект урока
 опорный каркас опорный каркас
 презентация урока презентация урока
 акселеративные методы акселеративные методы
 интерактивные технологии
Практика интерактивные технологии
Практика
 задачи и упражнения задачи и упражнения
 самопроверка самопроверка
 практикумы, тренинги, кейсы, квесты практикумы, тренинги, кейсы, квесты
 домашние задания домашние задания
 дискуссионные вопросы дискуссионные вопросы
 риторические вопросы от учеников
Иллюстрации риторические вопросы от учеников
Иллюстрации
 аудио-, видеоклипы и мультимедиа аудио-, видеоклипы и мультимедиа
 фотографии, картинки фотографии, картинки
 графики, таблицы, схемы графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты
Дополнения притчи, поговорки, кроссворды, цитаты
Дополнения
 рефераты рефераты
 статьи статьи
 фишки для любознательных фишки для любознательных
 шпаргалки шпаргалки
 учебники основные и дополнительные учебники основные и дополнительные
 словарь терминов словарь терминов
 прочие
Совершенствование учебников и уроков прочие
Совершенствование учебников и уроков
 исправление ошибок в учебнике исправление ошибок в учебнике
 обновление фрагмента в учебнике обновление фрагмента в учебнике
 элементы новаторства на уроке элементы новаторства на уроке
 замена устаревших знаний новыми
Только для учителей замена устаревших знаний новыми
Только для учителей
 идеальные уроки идеальные уроки
 календарный план на год календарный план на год
 методические рекомендации методические рекомендации
 программы программы
 обсуждения
Интегрированные уроки обсуждения
Интегрированные уроки
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.
|