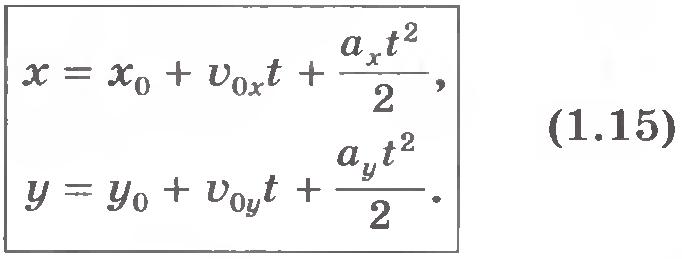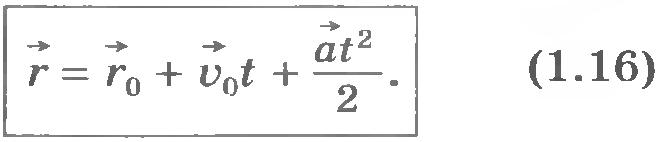|
|
|
| Строка 5: |
Строка 5: |
| | <metakeywords>Физика, 10 класс, Движение с, постоянным ускорением</metakeywords> | | <metakeywords>Физика, 10 класс, Движение с, постоянным ускорением</metakeywords> |
| | | | |
| - | Теперь получим уравнения, которые позволяют рассчитывать для этого движения положение точки в любой момент времени.<br> Допустим, движение с постоянным ускорением совершается в одной плоскости, пусть это будет плоскость ''ХОY''. Если вектор начальной скорости и вектор ускорения не лежат на одной прямой, то точка будет двигаться по кривой линии. Следовательно, в этом случае с течением времени будут изменяться обе ее координаты ''х'' и ''у''. Обозначим через ''x<sub>0</sub>'' и ''y<sub>0</sub>''координаты в начальный момент времени ''t<sub>0</sub>=0'', а через ''х'' и ''у'' координаты в момент времени ''t''. Тогда за время [[Image:a14-10.jpg]] изменения координат будут равны<br>[[Image:a14-1.jpg|center]]Отсюда<br>[[Image:a14-2.jpg|center]] Значит, для нахождения положения точки в любой момент времени надо знать ее начальные координаты и уметь находить изменения координат [[Image:a14-11.jpg]] и [[Image:a14-12.jpg]] за время движения.<br> В случае движения, при котором проекция скорости изменяется со временем (''рис.1.30''), величину [[Image:a14-11.jpg]], за время ''t'' можно найти следующим образом. Из § 8 мы знаем, что при равномерном движении изменение координаты точки за время [[Image:a14-13.jpg]] можно определить на графике зависимости [[Image:a14-14.jpg]] по площади прямоугольника. На рисунке 1.30 длина отрезка ''ОС'' численно равна времени движения. Разделим его на малые интервалы [[Image:a14-13.jpg]], в пределах которых проекцию скорости можно считать постоянной и равной ее среднему значению. Рассмотрим интервал [[Image:a14-15.jpg]]. Тогда [[Image:a14-16.jpg]], и соответственно площадь заштрихованного прямоугольника численно равна изменению координаты точки за время [[Image:a14-15.jpg]]. Сумма всех таких площадей численно равна изменению координаты точки за время ''t''. Чем меньше интервал [[Image:a14-13.jpg]], тем точнее будет результат. При стремлении [[Image:a14-13.jpg]] к нулю площадь фигуры ''АВСО'' будет стремиться к изменению координаты тела [[Image:a14-11.jpg]]. | + | Теперь получим уравнения, которые позволяют рассчитывать для этого движения положение точки в любой момент времени.<br> Допустим, движение с постоянным ускорением совершается в одной плоскости, пусть это будет плоскость ''ХОY''. Если вектор начальной скорости и вектор ускорения не лежат на одной прямой, то точка будет двигаться по кривой линии. Следовательно, в этом случае с течением времени будут изменяться обе ее координаты ''х'' и ''у''. Обозначим через ''x<sub>0</sub>'' и ''y<sub>0</sub>''координаты в начальный момент времени ''t<sub>0</sub>=0'', а через ''х'' и ''у'' координаты в момент времени ''t''. Тогда за время [[Image:A14-10.jpg|103x19px]] изменения координат будут равны<br>[[Image:A14-1.jpg|center|256x21px]]Отсюда<br>[[Image:A14-2.jpg|center|206x38px]] Значит, для нахождения положения точки в любой момент времени надо знать ее начальные координаты и уметь находить изменения координат [[Image:A14-11.jpg|25x15px]] и [[Image:A14-12.jpg|24x20px]] за время движения.<br> В случае движения, при котором проекция скорости изменяется со временем (''рис.1.30''), величину [[Image:A14-11.jpg|27x16px]], за время ''t'' можно найти следующим образом. Из § 8 мы знаем, что при равномерном движении изменение координаты точки за время [[Image:A14-13.jpg|24x18px]] можно определить на графике зависимости [[Image:A14-14.jpg|51x20px]] по площади прямоугольника. На рисунке 1.30 длина отрезка ''ОС'' численно равна времени движения. Разделим его на малые интервалы [[Image:A14-13.jpg|23x17px]], в пределах которых проекцию скорости можно считать постоянной и равной ее среднему значению. Рассмотрим интервал [[Image:A14-15.jpg|27x18px]]. Тогда [[Image:A14-16.jpg|111x22px]], и соответственно площадь заштрихованного прямоугольника численно равна изменению координаты точки за время [[Image:A14-15.jpg|27x18px]]. Сумма всех таких площадей численно равна изменению координаты точки за время ''t''. Чем меньше интервал [[Image:A14-13.jpg|21x16px]], тем точнее будет результат. При стремлении [[Image:A14-13.jpg|23x18px]] к нулю площадь фигуры ''АВСО'' будет стремиться к изменению координаты тела [[Image:A14-11.jpg|25x15px]]. |
| | | | |
| - | [[Image:a1.30.jpg|center]] В случае равноускоренного движения изменение координаты тела [[Image:a14-11.jpg]] численно равно площади трапеции ''АВСО''. Длины оснований ''ОА'' и ''ВС ''этой трапеции численно равны проекциям начальной и конечной скоростей, а длина высоты ''ОС'' - времени движения.<br> По формуле для площади трапеции имеем<br>[[Image:a14-3.jpg|center]] Учитывая, что [[Image:a14-4.jpg]], получаем<br>[[Image:a14-5.jpg|center]] Мы рассмотрели случай, когда [[Image:a14-17.jpg]] и [[Image:a14-18.jpg]]. Но полученная формула справедлива и тогда, когда одна из этих величин отрицательна или когда обе они отрицательны.<br> Изменение координаты [[Image:a14-12.jpg]] можно найти таким же способом, и оно имеет аналогичный вид<br>[[Image:a14-6.jpg|center]] Подставив найденные значения изменения координат [[Image:a14-11.jpg]] и [[Image:a14-12.jpg]] в формулы (1.14), получим выражения для координат при движении с постоянным ускорением как функции времени (их называют кинематическими уравнениями движения):<br>[[Image:a14-7.jpg|center]] Эти формулы применимы для описания как прямолинейного, так и криволинейного движения точки. Важно лишь, чтобы ускорение было постоянным.<br> Обычно в условиях задачи даются значения (модули) скоростей и ускорений. Поэтому удобнее, например, при движении точки по оси ''ОХ'' использовать уравнение [[Image:a14-8.jpg]], где [[Image:a14-19.jpg]] и ''a'' - модули начальной скорости и ускорения.<br> Очевидно, что в этом уравнении знак «+» берется тогда, когда направления скорости [[Image:a14-19.jpg]] и ускорения ''а'' совпадают с направлением оси ''ОХ'', знак «-» - когда они направлены в противоположную сторону.<br> При движении точки в плоскости ''ХОY'' двум уравнениям (1.15) соответствует одно векторное уравнение<br>[[Image:a14-9.jpg|center]] Обратите внимание на то, что с помощью формул (1.15) и (1.16) можно найти только положение движущейся точки в любой момент времени. Для нахождения пути необходимо более подробно исследовать траекторию, определить точки, в которых, возможно, произошло изменение направления движения.<br> Полученные уравнения, совместно с формулами для проекций скорости (1.13), позволяют решать любую задачу о движении с постоянным ускорением.<br> | + | [[Image:A1.30.jpg|center|176x165px]] В случае равноускоренного движения изменение координаты тела [[Image:A14-11.jpg|28x17px]] численно равно площади трапеции ''АВСО''. Длины оснований ''ОА'' и ''ВС ''этой трапеции численно равны проекциям начальной и конечной скоростей, а длина высоты ''ОС'' - времени движения.<br> По формуле для площади трапеции имеем<br>[[Image:A14-3.jpg|center|157x41px]] Учитывая, что [[Image:A14-4.jpg|142x22px]], получаем<br>[[Image:A14-5.jpg|center|343x42px]] Мы рассмотрели случай, когда [[Image:A14-17.jpg|62x19px]] и [[Image:A14-18.jpg|53x22px]]. Но полученная формула справедлива и тогда, когда одна из этих величин отрицательна или когда обе они отрицательны.<br> Изменение координаты [[Image:A14-12.jpg|25x21px]] можно найти таким же способом, и оно имеет аналогичный вид<br>[[Image:A14-6.jpg|center|155x45px]] Подставив найденные значения изменения координат [[Image:A14-11.jpg|27x16px]] и [[Image:A14-12.jpg|25x21px]] в формулы (1.14), получим выражения для координат при движении с постоянным ускорением как функции времени (их называют кинематическими уравнениями движения):<br>[[Image:A14-7.jpg|center|290x109px]] Эти формулы применимы для описания как прямолинейного, так и криволинейного движения точки. Важно лишь, чтобы ускорение было постоянным.<br> Обычно в условиях задачи даются значения (модули) скоростей и ускорений. Поэтому удобнее, например, при движении точки по оси ''ОХ'' использовать уравнение [[Image:A14-8.jpg|160x38px]], где [[Image:A14-19.jpg|21x17px]] и ''a'' - модули начальной скорости и ускорения.<br> Очевидно, что в этом уравнении знак «+» берется тогда, когда направления скорости [[Image:A14-19.jpg|21x18px]] и ускорения ''а'' совпадают с направлением оси ''ОХ'', знак «-» - когда они направлены в противоположную сторону.<br> При движении точки в плоскости ''ХОY'' двум уравнениям (1.15) соответствует одно векторное уравнение<br>[[Image:A14-9.jpg|center|264x56px]] Обратите внимание на то, что с помощью формул (1.15) и (1.16) можно найти только положение движущейся точки в любой момент времени. Для нахождения пути необходимо более подробно исследовать траекторию, определить точки, в которых, возможно, произошло изменение направления движения.<br> Полученные уравнения, совместно с формулами для проекций скорости (1.13), позволяют решать любую задачу о движении с постоянным ускорением.<br> |
| | | | |
| - | | + | <br> ''Г.Я.Мякишев, Б.Б.Буховцев, Н.Н.Сотский, Физика 10 класс'' |
| - | ''Г.Я.Мякишев, Б.Б.Буховцев, Н.Н.Сотский, Физика 10 класс'' | + | |
| | | | |
| | <br> <sub>Скачать календарно-тематическое планирование [[Физика и астрономия|по физике]], ответы на тесты, задания и ответы школьнику, [[Гипермаркет знаний - первый в мире!|книги и учебники]], курсы учителю [[Физика 10 класс|по физике для 10 класса]]</sub> | | <br> <sub>Скачать календарно-тематическое планирование [[Физика и астрономия|по физике]], ответы на тесты, задания и ответы школьнику, [[Гипермаркет знаний - первый в мире!|книги и учебники]], курсы учителю [[Физика 10 класс|по физике для 10 класса]]</sub> |
Версия 18:41, 3 августа 2010
Гипермаркет знаний>>Физика и астрономия>>Физика 10 класс>>Физика: Движение с постоянным ускорением
Теперь получим уравнения, которые позволяют рассчитывать для этого движения положение точки в любой момент времени.
Допустим, движение с постоянным ускорением совершается в одной плоскости, пусть это будет плоскость ХОY. Если вектор начальной скорости и вектор ускорения не лежат на одной прямой, то точка будет двигаться по кривой линии. Следовательно, в этом случае с течением времени будут изменяться обе ее координаты х и у. Обозначим через x0 и y0координаты в начальный момент времени t0=0, а через х и у координаты в момент времени t. Тогда за время  изменения координат будут равны изменения координат будут равны
Отсюда
Значит, для нахождения положения точки в любой момент времени надо знать ее начальные координаты и уметь находить изменения координат  и и  за время движения. за время движения.
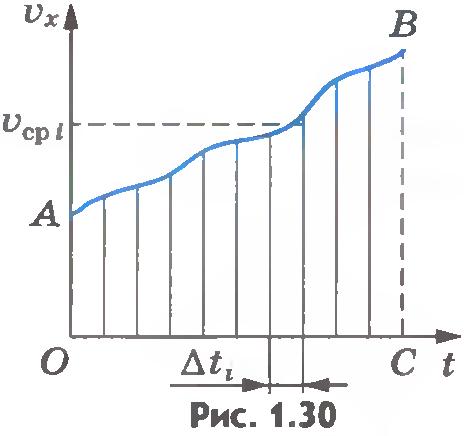
В случае движения, при котором проекция скорости изменяется со временем (рис.1.30), величину  , за время t можно найти следующим образом. Из § 8 мы знаем, что при равномерном движении изменение координаты точки за время , за время t можно найти следующим образом. Из § 8 мы знаем, что при равномерном движении изменение координаты точки за время  можно определить на графике зависимости можно определить на графике зависимости 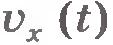 по площади прямоугольника. На рисунке 1.30 длина отрезка ОС численно равна времени движения. Разделим его на малые интервалы по площади прямоугольника. На рисунке 1.30 длина отрезка ОС численно равна времени движения. Разделим его на малые интервалы  , в пределах которых проекцию скорости можно считать постоянной и равной ее среднему значению. Рассмотрим интервал , в пределах которых проекцию скорости можно считать постоянной и равной ее среднему значению. Рассмотрим интервал  . Тогда . Тогда  , и соответственно площадь заштрихованного прямоугольника численно равна изменению координаты точки за время , и соответственно площадь заштрихованного прямоугольника численно равна изменению координаты точки за время  . Сумма всех таких площадей численно равна изменению координаты точки за время t. Чем меньше интервал . Сумма всех таких площадей численно равна изменению координаты точки за время t. Чем меньше интервал  , тем точнее будет результат. При стремлении , тем точнее будет результат. При стремлении  к нулю площадь фигуры АВСО будет стремиться к изменению координаты тела к нулю площадь фигуры АВСО будет стремиться к изменению координаты тела  .
В случае равноускоренного движения изменение координаты тела .
В случае равноускоренного движения изменение координаты тела  численно равно площади трапеции АВСО. Длины оснований ОА и ВС этой трапеции численно равны проекциям начальной и конечной скоростей, а длина высоты ОС - времени движения. численно равно площади трапеции АВСО. Длины оснований ОА и ВС этой трапеции численно равны проекциям начальной и конечной скоростей, а длина высоты ОС - времени движения.
По формуле для площади трапеции имеем
Учитывая, что 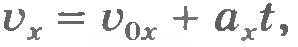 , получаем , получаем
Мы рассмотрели случай, когда  и и 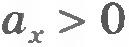 . Но полученная формула справедлива и тогда, когда одна из этих величин отрицательна или когда обе они отрицательны. . Но полученная формула справедлива и тогда, когда одна из этих величин отрицательна или когда обе они отрицательны.
Изменение координаты  можно найти таким же способом, и оно имеет аналогичный вид можно найти таким же способом, и оно имеет аналогичный вид
Подставив найденные значения изменения координат  и и  в формулы (1.14), получим выражения для координат при движении с постоянным ускорением как функции времени (их называют кинематическими уравнениями движения): в формулы (1.14), получим выражения для координат при движении с постоянным ускорением как функции времени (их называют кинематическими уравнениями движения):
Эти формулы применимы для описания как прямолинейного, так и криволинейного движения точки. Важно лишь, чтобы ускорение было постоянным.
Обычно в условиях задачи даются значения (модули) скоростей и ускорений. Поэтому удобнее, например, при движении точки по оси ОХ использовать уравнение 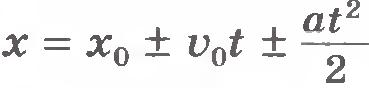 , где , где 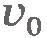 и a - модули начальной скорости и ускорения. и a - модули начальной скорости и ускорения.
Очевидно, что в этом уравнении знак «+» берется тогда, когда направления скорости 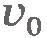 и ускорения а совпадают с направлением оси ОХ, знак «-» - когда они направлены в противоположную сторону. и ускорения а совпадают с направлением оси ОХ, знак «-» - когда они направлены в противоположную сторону.
При движении точки в плоскости ХОY двум уравнениям (1.15) соответствует одно векторное уравнение
Обратите внимание на то, что с помощью формул (1.15) и (1.16) можно найти только положение движущейся точки в любой момент времени. Для нахождения пути необходимо более подробно исследовать траекторию, определить точки, в которых, возможно, произошло изменение направления движения.
Полученные уравнения, совместно с формулами для проекций скорости (1.13), позволяют решать любую задачу о движении с постоянным ускорением.
Г.Я.Мякишев, Б.Б.Буховцев, Н.Н.Сотский, Физика 10 класс
Скачать календарно-тематическое планирование по физике, ответы на тесты, задания и ответы школьнику, книги и учебники, курсы учителю по физике для 10 класса
Содержание урока
 конспект урока конспект урока
 опорный каркас опорный каркас
 презентация урока презентация урока
 акселеративные методы акселеративные методы
 интерактивные технологии
Практика интерактивные технологии
Практика
 задачи и упражнения задачи и упражнения
 самопроверка самопроверка
 практикумы, тренинги, кейсы, квесты практикумы, тренинги, кейсы, квесты
 домашние задания домашние задания
 дискуссионные вопросы дискуссионные вопросы
 риторические вопросы от учеников
Иллюстрации риторические вопросы от учеников
Иллюстрации
 аудио-, видеоклипы и мультимедиа аудио-, видеоклипы и мультимедиа
 фотографии, картинки фотографии, картинки
 графики, таблицы, схемы графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты
Дополнения притчи, поговорки, кроссворды, цитаты
Дополнения
 рефераты рефераты
 статьи статьи
 фишки для любознательных фишки для любознательных
 шпаргалки шпаргалки
 учебники основные и дополнительные учебники основные и дополнительные
 словарь терминов словарь терминов
 прочие
Совершенствование учебников и уроков прочие
Совершенствование учебников и уроков
 исправление ошибок в учебнике исправление ошибок в учебнике
 обновление фрагмента в учебнике обновление фрагмента в учебнике
 элементы новаторства на уроке элементы новаторства на уроке
 замена устаревших знаний новыми
Только для учителей замена устаревших знаний новыми
Только для учителей
 идеальные уроки идеальные уроки
 календарный план на год календарный план на год
 методические рекомендации методические рекомендации
 программы программы
 обсуждения
Интегрированные уроки обсуждения
Интегрированные уроки
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.
|