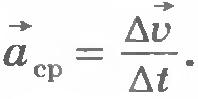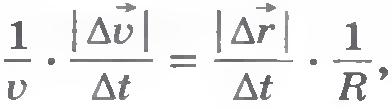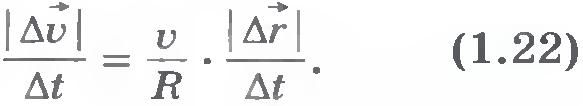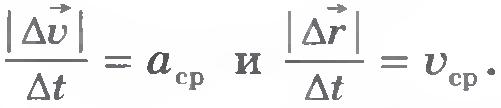|
|
|
| Строка 5: |
Строка 5: |
| | <metakeywords>Физика, 10 класс, Равномерное движение, точки по окружности</metakeywords> | | <metakeywords>Физика, 10 класс, Равномерное движение, точки по окружности</metakeywords> |
| | | | |
| - | Движение тела по окружности или дуге окружности довольно часто встречается в природе и технике. Приблизительно по окружности движется Луна вокруг Земли; каждая точка земной поверхности движется по окружности вокруг земной оси; дуги окружности описывают различные точки самолета во время виража, автомобиля при повороте, поезда на закруглении дороги и т. д. Поэтому знакомство с таким движением имеет большое значение.<br> Рассмотрим равномерное движение тела по окружности. Это такое движение, при котором скорость и ускорение не меняются по модулю, а изменяются лишь по направлению.<br> Найдем модуль и направление вектора ускорения при равномерном движении точки по окружности радиусом ''R''. Пусть точка в момент времени ''t ''занимает положение ''М'', а через интервал времени [[Image:a17-7.jpg]] - положение ''M<sub>1</sub>'' (''рис.1.41''). <br>[[Image:a1.41.jpg|center]]Обозначим ее скорость в положении ''M'' через [[Image:a17-8.jpg]], а в положении ''M<sub>1</sub>'' через [[Image:a17-9.jpg]]. При равномерном движении [[Image:a17-10.jpg]]. Чтобы найти изменение скорости [[Image:a17-11.jpg]] за время [[Image:a17-7.jpg]], надо из вектора [[Image:a17-9.jpg]] вычесть вектор [[Image:a17-8.jpg]]. Разделив вектор [[Image:a17-11.jpg]] на промежуток времени [[Image:a17-7.jpg]], получим среднее ускорение точки за этот промежуток времени:<br>[[Image:a17-1.jpg|center]]При стремлении интервала [[Image:a17-7.jpg]] к нулю вектор среднего ускорения стремится в пределе к определенному вектору, называемому вектором мгновенного ускорения (см. § 11).<br> Сначала найдем модуль мгновенного ускорения. Для этого проведем вектор перемещения [[Image:a17-12.jpg]] и рассмотрим треугольники ''OMM<sub>1</sub>''<sub></sub>и ''M<sub>1</sub>AB''. Эти треугольники подобны как равнобедренные с равными углами при вершинах. Следовательно [[Image:a17-2.jpg]].<br> Разделив левую и правую части этого равенства на промежуток времени [[Image:a17-7.jpg]], получим<br>[[Image:a17-3.jpg|center]]или<br>[[Image:a17-4.jpg|center]]Но<br>[[Image:a17-5.jpg|center]]В пределе, т. е. при стремлении промежутка времени [[Image:a17-7.jpg]] к нулю, модуль вектора [[Image:a17-13.jpg]] будет не чем иным, как модулем ускорения [[Image:a17-14.jpg]] точки в момент времени ''t'', а модуль вектора будет представлять собой модуль вектора мгновенной скорости ****.Тогда равенство (1.22) примет вид<br><br>Так как **** и ***** постоянны, то модуль вектора ускорения при равномерном движении точки по окружности остается все время неизменным.<br> Найдем теперь направление ускорения ***. Вектор ускорения направлен так, как направлен вектор ***** в пределе при стремлении промежутка времени **** к нулю. Из рисун¬ка 1.41 видно, что при стремлении интервала **** к нулю точка ****приближается к точке***** и угол ***** стремится к нулю. Следовательно, угол **** стремится к 90°. Таким образом, угол между вектором ***** и радиусом окружности стремится к нулю. Следовательно в пределе вектор мгно¬венного ускорения направлен к центру окружности. По¬этому ускорение точки при ее равномерном движении по окружности называют центростремительным.<br>Так как в процессе движения точки по окружности ускорение все время направлено по радиусу к центру, то оно непрерывно изменяется по направлению. Следователь¬но, равномерное движение точки по окружности является движением с переменным ускорением и переменной скоро¬стью. Отметим, что модули скорости и ускорения при этом остаются постоянными.<br><br><br>???<br>1. Точка движется равномерно по окружности. Постоянна ли ее скорость?<br>2. Постоянно ли ускорение при равномерном движении точки по окружности?<br>3. Куда направлено ускорение конца стрелки часов?<br> | + | Движение тела по окружности или дуге окружности довольно часто встречается в природе и технике. Приблизительно по окружности движется Луна вокруг Земли; каждая точка земной поверхности движется по окружности вокруг земной оси; дуги окружности описывают различные точки самолета во время виража, автомобиля при повороте, поезда на закруглении дороги и т. д. Поэтому знакомство с таким движением имеет большое значение.<br> Рассмотрим равномерное движение тела по окружности. Это такое движение, при котором скорость и ускорение не меняются по модулю, а изменяются лишь по направлению.<br> Найдем модуль и направление вектора ускорения при равномерном движении точки по окружности радиусом ''R''. Пусть точка в момент времени ''t ''занимает положение ''М'', а через интервал времени [[Image:A17-7.jpg]] - положение ''M<sub>1</sub>'' (''рис.1.41''). <br>[[Image:A1.41.jpg|center]]Обозначим ее скорость в положении ''M'' через [[Image:A17-8.jpg]], а в положении ''M<sub>1</sub>'' через [[Image:A17-9.jpg]]. При равномерном движении [[Image:A17-10.jpg]]. Чтобы найти изменение скорости [[Image:A17-11.jpg]] за время [[Image:A17-7.jpg]], надо из вектора [[Image:A17-9.jpg]] вычесть вектор [[Image:A17-8.jpg]]. Разделив вектор [[Image:A17-11.jpg]] на промежуток времени [[Image:A17-7.jpg]], получим среднее ускорение точки за этот промежуток времени:<br>[[Image:A17-1.jpg|center]]При стремлении интервала [[Image:A17-7.jpg]] к нулю вектор среднего ускорения стремится в пределе к определенному вектору, называемому вектором мгновенного ускорения (см. § 11).<br> Сначала найдем модуль мгновенного ускорения. Для этого проведем вектор перемещения [[Image:A17-12.jpg]] и рассмотрим треугольники ''OMM<sub>1</sub>''<sub></sub>и ''M<sub>1</sub>AB''. Эти треугольники подобны как равнобедренные с равными углами при вершинах. Следовательно [[Image:A17-2.jpg]].<br> Разделив левую и правую части этого равенства на промежуток времени [[Image:A17-7.jpg]], получим<br>[[Image:A17-3.jpg|center]]или<br>[[Image:A17-4.jpg|center]]Но<br>[[Image:A17-5.jpg|center]]В пределе, т. е. при стремлении промежутка времени [[Image:A17-7.jpg]] к нулю, модуль вектора [[Image:A17-13.jpg]] будет не чем иным, как модулем ускорения [[Image:A17-14.jpg]] точки в момент времени ''t'', а модуль вектора [[Image:a17-15.jpg]] будет представлять собой модуль вектора мгновенной скорости [[Image:a17-16.jpg]].Тогда равенство (1.22) примет вид<br>[[Image:f17-6.jpg|center]]Так как ''v'' и ''R'' постоянны, то модуль вектора ускорения при равномерном движении точки по окружности остается все время неизменным.<br> Найдем теперь направление ускорения [[Image:a17-17.jpg]]. Вектор ускорения направлен так, как направлен вектор [[Image:a17-11.jpg]] в пределе при стремлении промежутка времени [[Image:a17-7.jpg]] к нулю. Из рисунка 1.41 видно, что при стремлении интервала [[Image:a17-7.jpg]] к нулю точка ''M<sub>1</sub>'' приближается к точке ''M'' и угол [[Image:a1-18.jpg]] стремится к нулю. Следовательно, угол ''BM<sub>1</sub>A ''стремится к 90°. Таким образом, угол между вектором [[Image:a17-11.jpg]] и радиусом окружности стремится к нулю. Следовательно в пределе вектор мгновенного ускорения направлен к центру окружности. Поэтому ускорение точки при ее равномерном движении по окружности называют '''центростремительным'''.<br> Так как в процессе движения точки по окружности ускорение все время направлено по радиусу к центру, то оно непрерывно изменяется по направлению. Следовательно, равномерное движение точки по окружности является движением с переменным ускорением и переменной скоростью. Отметим, что модули скорости и ускорения при этом остаются постоянными.<br><br><br> ???<br> 1. Точка движется равномерно по окружности. Постоянна ли ее скорость?<br> 2. Постоянно ли ускорение при равномерном движении точки по окружности?<br> 3. Куда направлено ускорение конца стрелки часов?<br> |
| | | | |
| - | | + | <br> ''Г.Я.Мякишев, Б.Б.Буховцев, Н.Н.Сотский, Физика 10 класс'' |
| - | ''Г.Я.Мякишев, Б.Б.Буховцев, Н.Н.Сотский, Физика 10 класс'' | + | |
| | | | |
| | <br> <sub>Полный список тем [[Физика и астрономия|по физике]], календарный план по всем предметам согласно [[Гипермаркет знаний - первый в мире!|школьной программы]], домашнее задание, курсы и задание [[Физика 10 класс|по физике для 10 класса]]</sub> | | <br> <sub>Полный список тем [[Физика и астрономия|по физике]], календарный план по всем предметам согласно [[Гипермаркет знаний - первый в мире!|школьной программы]], домашнее задание, курсы и задание [[Физика 10 класс|по физике для 10 класса]]</sub> |
Версия 21:06, 3 августа 2010
Гипермаркет знаний>>Физика и астрономия>>Физика 10 класс>>Физика: Равномерное движение точки по окружности
Движение тела по окружности или дуге окружности довольно часто встречается в природе и технике. Приблизительно по окружности движется Луна вокруг Земли; каждая точка земной поверхности движется по окружности вокруг земной оси; дуги окружности описывают различные точки самолета во время виража, автомобиля при повороте, поезда на закруглении дороги и т. д. Поэтому знакомство с таким движением имеет большое значение.
Рассмотрим равномерное движение тела по окружности. Это такое движение, при котором скорость и ускорение не меняются по модулю, а изменяются лишь по направлению.
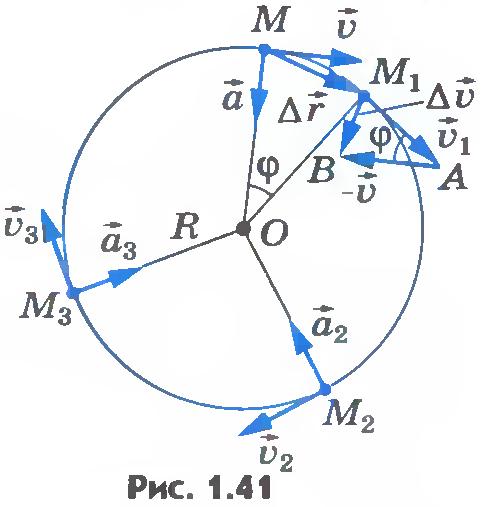
Найдем модуль и направление вектора ускорения при равномерном движении точки по окружности радиусом R. Пусть точка в момент времени t занимает положение М, а через интервал времени  - положение M1 (рис.1.41). - положение M1 (рис.1.41).
Обозначим ее скорость в положении M через  , а в положении M1 через , а в положении M1 через 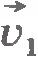 . При равномерном движении . При равномерном движении  . Чтобы найти изменение скорости . Чтобы найти изменение скорости 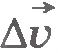 за время за время  , надо из вектора , надо из вектора 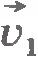 вычесть вектор вычесть вектор  . Разделив вектор . Разделив вектор 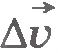 на промежуток времени на промежуток времени  , получим среднее ускорение точки за этот промежуток времени: , получим среднее ускорение точки за этот промежуток времени:
При стремлении интервала  к нулю вектор среднего ускорения стремится в пределе к определенному вектору, называемому вектором мгновенного ускорения (см. § 11). к нулю вектор среднего ускорения стремится в пределе к определенному вектору, называемому вектором мгновенного ускорения (см. § 11).
Сначала найдем модуль мгновенного ускорения. Для этого проведем вектор перемещения  и рассмотрим треугольники OMM1и M1AB. Эти треугольники подобны как равнобедренные с равными углами при вершинах. Следовательно и рассмотрим треугольники OMM1и M1AB. Эти треугольники подобны как равнобедренные с равными углами при вершинах. Следовательно 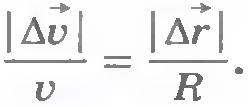 . .
Разделив левую и правую части этого равенства на промежуток времени  , получим , получим
или
Но
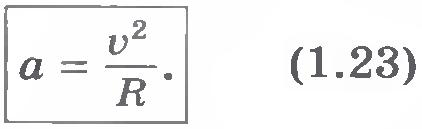
В пределе, т. е. при стремлении промежутка времени  к нулю, модуль вектора к нулю, модуль вектора 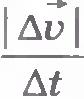 будет не чем иным, как модулем ускорения будет не чем иным, как модулем ускорения 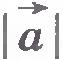 точки в момент времени t, а модуль вектора точки в момент времени t, а модуль вектора 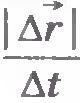 будет представлять собой модуль вектора мгновенной скорости будет представлять собой модуль вектора мгновенной скорости 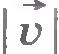 .Тогда равенство (1.22) примет вид .Тогда равенство (1.22) примет вид
Так как v и R постоянны, то модуль вектора ускорения при равномерном движении точки по окружности остается все время неизменным.
Найдем теперь направление ускорения 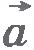 . Вектор ускорения направлен так, как направлен вектор . Вектор ускорения направлен так, как направлен вектор 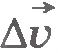 в пределе при стремлении промежутка времени в пределе при стремлении промежутка времени  к нулю. Из рисунка 1.41 видно, что при стремлении интервала к нулю. Из рисунка 1.41 видно, что при стремлении интервала  к нулю точка M1 приближается к точке M и угол к нулю точка M1 приближается к точке M и угол 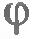 стремится к нулю. Следовательно, угол BM1A стремится к 90°. Таким образом, угол между вектором стремится к нулю. Следовательно, угол BM1A стремится к 90°. Таким образом, угол между вектором 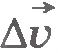 и радиусом окружности стремится к нулю. Следовательно в пределе вектор мгновенного ускорения направлен к центру окружности. Поэтому ускорение точки при ее равномерном движении по окружности называют центростремительным. и радиусом окружности стремится к нулю. Следовательно в пределе вектор мгновенного ускорения направлен к центру окружности. Поэтому ускорение точки при ее равномерном движении по окружности называют центростремительным.
Так как в процессе движения точки по окружности ускорение все время направлено по радиусу к центру, то оно непрерывно изменяется по направлению. Следовательно, равномерное движение точки по окружности является движением с переменным ускорением и переменной скоростью. Отметим, что модули скорости и ускорения при этом остаются постоянными.
???
1. Точка движется равномерно по окружности. Постоянна ли ее скорость?
2. Постоянно ли ускорение при равномерном движении точки по окружности?
3. Куда направлено ускорение конца стрелки часов?
Г.Я.Мякишев, Б.Б.Буховцев, Н.Н.Сотский, Физика 10 класс
Полный список тем по физике, календарный план по всем предметам согласно школьной программы, домашнее задание, курсы и задание по физике для 10 класса
Содержание урока
 конспект урока конспект урока
 опорный каркас опорный каркас
 презентация урока презентация урока
 акселеративные методы акселеративные методы
 интерактивные технологии
Практика интерактивные технологии
Практика
 задачи и упражнения задачи и упражнения
 самопроверка самопроверка
 практикумы, тренинги, кейсы, квесты практикумы, тренинги, кейсы, квесты
 домашние задания домашние задания
 дискуссионные вопросы дискуссионные вопросы
 риторические вопросы от учеников
Иллюстрации риторические вопросы от учеников
Иллюстрации
 аудио-, видеоклипы и мультимедиа аудио-, видеоклипы и мультимедиа
 фотографии, картинки фотографии, картинки
 графики, таблицы, схемы графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты
Дополнения притчи, поговорки, кроссворды, цитаты
Дополнения
 рефераты рефераты
 статьи статьи
 фишки для любознательных фишки для любознательных
 шпаргалки шпаргалки
 учебники основные и дополнительные учебники основные и дополнительные
 словарь терминов словарь терминов
 прочие
Совершенствование учебников и уроков прочие
Совершенствование учебников и уроков
 исправление ошибок в учебнике исправление ошибок в учебнике
 обновление фрагмента в учебнике обновление фрагмента в учебнике
 элементы новаторства на уроке элементы новаторства на уроке
 замена устаревших знаний новыми
Только для учителей замена устаревших знаний новыми
Только для учителей
 идеальные уроки идеальные уроки
 календарный план на год календарный план на год
 методические рекомендации методические рекомендации
 программы программы
 обсуждения
Интегрированные уроки обсуждения
Интегрированные уроки
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.
|
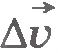 за время
за время 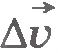 на промежуток времени
на промежуток времени 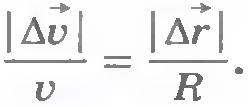 .
.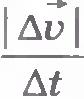 будет не чем иным, как модулем ускорения
будет не чем иным, как модулем ускорения 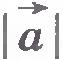 точки в момент времени t, а модуль вектора
точки в момент времени t, а модуль вектора 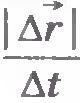 будет представлять собой модуль вектора мгновенной скорости
будет представлять собой модуль вектора мгновенной скорости 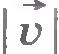 .Тогда равенство (1.22) примет вид
.Тогда равенство (1.22) примет вид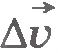 в пределе при стремлении промежутка времени
в пределе при стремлении промежутка времени 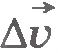 и радиусом окружности стремится к нулю. Следовательно в пределе вектор мгновенного ускорения направлен к центру окружности. Поэтому ускорение точки при ее равномерном движении по окружности называют центростремительным.
и радиусом окружности стремится к нулю. Следовательно в пределе вектор мгновенного ускорения направлен к центру окружности. Поэтому ускорение точки при ее равномерном движении по окружности называют центростремительным.