|
|
|
| Строка 1: |
Строка 1: |
| | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Информатика|Информатика]]>>[[Информатика 11 класс|Информатика 11 класс]]>>Информатика: О статистике и статистических данных''' | | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Информатика|Информатика]]>>[[Информатика 11 класс|Информатика 11 класс]]>>Информатика: О статистике и статистических данных''' |
| | | | |
| - | <br><metakeywords>О статистике и статистических данных</metakeywords> | + | <br><metakeywords>О статистике и статистических данных</metakeywords> |
| | | | |
| | + | <br> |
| | | | |
| | + | ''' О статистике и статистических данных''' |
| | | | |
| - | ''' О статистике и статистических данных'''
| + | <br> '' Рассмотрим способ нахождения зависимости частоты заболеваемости жителей города бронхиальной астмой от качества воздуха (третья задача из сформулированных в начале предыдущего параграфа). Любому человеку понятно, что такая зависимость существует. Очевидно, что чем хуже воздух, тем больше больных астмой. Но это качественное заключение. '' |
| | | | |
| | + | '' Его недостаточно для того, чтобы управлять уровнем загрязненности воздуха . Для управления требуются более конкретные знания. Нужно установить, какие именно примеси сильнее всего влияют на здоровье людей, как связана концентрация этих примесей в воздухе с числом заболеваний. Такую зависимость можно установить только экспериментальным путем: путем сбора многочисленных данных, их анализа и обобщения.'' |
| | | | |
| - | '' Рассмотрим способ нахождения зависимости частоты заболеваемости жителей города бронхиальной астмой от качества воздуха (третья задача из сформулированных в начале предыдущего параграфа). Любому человеку понятно, что такая зависимость существует. Очевидно, что чем хуже воздух, тем больше больных астмой. Но это качественное заключение. '' | + | '' В таких ситуациях на помощь приходит статистика: паука о сборе, измерении и анализе массовых количественных данных. Существуют медицинская статистика, экономическая статистика , социальная статистика и другие Математический аппарат статистики разрабатывает раздел науки под названием «Математическая статистикам».'' |
| | | | |
| - | '' Его недостаточно для того, чтобы управлять уровнем загрязненности воздуха . Для управления требуются более конкретные знания. Нужно установить, какие именно примеси сильнее всего влияют на здоровье людей, как связана концентрация этих примесей в воздухе с числом заболеваний. Такую зависимость можно установить только экспериментальным путем: путем сбора многочисленных данных, их анализа и обобщения.'' | + | '' Рассмотрим пример из области медицинской статистики. Известно, что наиболее сильное влияние на бронхиально-легочные заболевания оказывает угарный газ — оксид углерода. Поставив цель определить эту зависимость, специалисты по медицинской статистике проводят сбор данных. Они собирают сведения из разных городов о средней концентрации угарного газа в атмосфере и о заболеваемости астмой (число хронических больных на 1000 жителей). Полученные данные можно свести в таблицу, а также представить в виде точечной диаграммы (рис. 2.12) .'' |
| | | | |
| - | '' В таких ситуациях на помощь приходит статистика: паука о сборе, измерении и анализе массовых количественных данных. Существуют медицинская статистика, экономическая статистика , социальная статистика и другие Математический аппарат статистики разрабатывает раздел науки под названием «Математическая статистикам».''
| + | '' Статистические данные всегда являются приближенными, усредненными. Поэтому они носят оценочный характер. Однако они верно отражают характер зависимости величин. И еще одно важное замечание: для достоверности результатов, полученных путем анализа статистических данных, этих данных должно быть много.<br> <br>[[Image:инф94.jpg]]<br><br>Рис. 2.12. Табличное и графическое представление статистических данных<br><br>Из полученных данных можно сделать вывод, что при концентрации угарного газа до 3 мг/куб. м его влияние на заболеваемость астмой несильное. С дальнейшим ростом концентрации наступает резкий рост заболеваемости.<br>А как построить математическую модель данного явле¬ния? Очевидно, нужно получить формулу, отражающую за¬висимость числа хронических больных Р от концентрации угарного газа С. На языке математики зто называется функ¬цией зависимости Р от С: Р(С). Вид такой функции неизвес¬тен, ее следует искать методом подбора по эксперименталь¬ным данным.<br>-Понятно нтсл ЛтдоцЬик .искомой 1|*ушкдгаи ^1ЛЛЖЙР луюхр-дить близко к точкам диаграммы экспериментальных дан¬ных* Строить функцию так, чтобы ее график точно прохо¬дил через все данные точки (рис. 2.13 а), не имеет смысла. Во-первых, математический вид такой функции может ока¬заться слишком сложным. Во-вторых, уже говорилось о том, что зксцериментальные значения являются прибли¬женными.<br>Отсюда следуют основные требования к искомой функ¬ции:<br>• она должна быть достаточно простой для использования ее в дальнейших вычислениях;<br>• график этой функции должен проходить вблизи экспери¬ментальных точек так, чтобы отклонения этих точек от графика были минимальны и равномерны (рис. 2.13 б).<br>Подученную функцию, график которой приведен на рис. 2.13 tf, принято называть в статистике регрессионной моделью.<br> <br>а) б)<br><br>Рис. 2.13. Два варианта построения графической зависимости<br>по экспериментальным данным<br><br><br>Коротко о главном<br><br><br>Статистика: наука о сборе, измерении и анализе массо¬вых количественных данных.<br>Статистические данные носят приближенный, усреднен¬ный характер, получаются путем многократных измерений.<br>Регрессионная модель — это функция, описывающая за¬висимость между количественными характеристиками сложных систем. Вид регрессионной функции определяется путем подбора по экспериментальным данным.<br><br><br>Вопросы и задания<br><br><br>1. а) Что такое статистика?<br>б) Являются ли результаты статистических расчетов точными?<br>в) Что такое регрессионная модель?<br>2. Какие из следующих величин можно назвать статистическими:<br>температура вашего тела в данный момент, средняя температу-<br>ра в вашей регионе за последний месяц; максимальная ско-<br>рость, развиваемая данной моделью автомобиля; среднее число<br>осадков, выпавших в вашем регионе в течение года.''<br><br>''Семакин И.Г., Хеннер Е.К., Информатика и ИКТ, 11'' |
| - | | + | |
| - | '' Рассмотрим пример из области медицинской статистики. Известно, что наиболее сильное влияние на бронхиально-легочные заболевания оказывает угарный газ — оксид углерода. Поставив цель определить эту зависимость, специалисты по медицинской статистике проводят сбор данных. Они собирают сведения из разных городов о средней концентрации угарного газа в атмосфере и о заболеваемости астмой (число хронических больных на 1000 жителей). Полученные данные можно свести в таблицу, а также представить в виде точечной диаграммы (рис. 2.12) .''
| + | |
| - | | + | |
| - | '' Статистические данные всегда являются приближенными, усредненными. Поэтому они носят оценочный характер. Однако они верно отражают характер зависимости величин. И еще одно важное замечание: для достоверности результатов, полученных путем анализа статистических данных, этих данных должно быть много.<br> <br><br><br>Рис. 2.12. Табличное и графическое представление статистических данных<br><br>Из полученных данных можно сделать вывод, что при концентрации угарного газа до 3 мг/куб. м его влияние на заболеваемость астмой несильное. С дальнейшим ростом концентрации наступает резкий рост заболеваемости.<br>А как построить математическую модель данного явле¬ния? Очевидно, нужно получить формулу, отражающую за¬висимость числа хронических больных Р от концентрации угарного газа С. На языке математики зто называется функ¬цией зависимости Р от С: Р(С). Вид такой функции неизвес¬тен, ее следует искать методом подбора по эксперименталь¬ным данным.<br>-Понятно нтсл ЛтдоцЬик .искомой 1|*ушкдгаи ^1ЛЛЖЙР луюхр-дить близко к точкам диаграммы экспериментальных дан¬ных* Строить функцию так, чтобы ее график точно прохо¬дил через все данные точки (рис. 2.13 а), не имеет смысла. Во-первых, математический вид такой функции может ока¬заться слишком сложным. Во-вторых, уже говорилось о том, что зксцериментальные значения являются прибли¬женными.<br>Отсюда следуют основные требования к искомой функ¬ции:<br>• она должна быть достаточно простой для использования ее в дальнейших вычислениях;<br>• график этой функции должен проходить вблизи экспери¬ментальных точек так, чтобы отклонения этих точек от графика были минимальны и равномерны (рис. 2.13 б).<br>Подученную функцию, график которой приведен на рис. 2.13 tf, принято называть в статистике регрессионной моделью.<br> <br>а) б)<br><br>Рис. 2.13. Два варианта построения графической зависимости<br>по экспериментальным данным<br><br><br>Коротко о главном<br><br><br>Статистика: наука о сборе, измерении и анализе массо¬вых количественных данных.<br>Статистические данные носят приближенный, усреднен¬ный характер, получаются путем многократных измерений.<br>Регрессионная модель — это функция, описывающая за¬висимость между количественными характеристиками сложных систем. Вид регрессионной функции определяется путем подбора по экспериментальным данным.<br><br><br>Вопросы и задания<br><br><br>1. а) Что такое статистика?<br>б) Являются ли результаты статистических расчетов точными?<br>в) Что такое регрессионная модель?<br>2. Какие из следующих величин можно назвать статистическими:<br>температура вашего тела в данный момент, средняя температу-<br>ра в вашей регионе за последний месяц; максимальная ско-<br>рость, развиваемая данной моделью автомобиля; среднее число<br>осадков, выпавших в вашем регионе в течение года.''<br><br>''Семакин И.Г., Хеннер Е.К., Информатика и ИКТ, 11'' | + | |
| | | | |
| | ''Отослано читателями из интернет-сайтов''<br><br> | | ''Отослано читателями из интернет-сайтов''<br><br> |
Версия 18:34, 19 августа 2010
Гипермаркет знаний>>Информатика>>Информатика 11 класс>>Информатика: О статистике и статистических данных
О статистике и статистических данных
Рассмотрим способ нахождения зависимости частоты заболеваемости жителей города бронхиальной астмой от качества воздуха (третья задача из сформулированных в начале предыдущего параграфа). Любому человеку понятно, что такая зависимость существует. Очевидно, что чем хуже воздух, тем больше больных астмой. Но это качественное заключение.
Его недостаточно для того, чтобы управлять уровнем загрязненности воздуха . Для управления требуются более конкретные знания. Нужно установить, какие именно примеси сильнее всего влияют на здоровье людей, как связана концентрация этих примесей в воздухе с числом заболеваний. Такую зависимость можно установить только экспериментальным путем: путем сбора многочисленных данных, их анализа и обобщения.
В таких ситуациях на помощь приходит статистика: паука о сборе, измерении и анализе массовых количественных данных. Существуют медицинская статистика, экономическая статистика , социальная статистика и другие Математический аппарат статистики разрабатывает раздел науки под названием «Математическая статистикам».
Рассмотрим пример из области медицинской статистики. Известно, что наиболее сильное влияние на бронхиально-легочные заболевания оказывает угарный газ — оксид углерода. Поставив цель определить эту зависимость, специалисты по медицинской статистике проводят сбор данных. Они собирают сведения из разных городов о средней концентрации угарного газа в атмосфере и о заболеваемости астмой (число хронических больных на 1000 жителей). Полученные данные можно свести в таблицу, а также представить в виде точечной диаграммы (рис. 2.12) .
Статистические данные всегда являются приближенными, усредненными. Поэтому они носят оценочный характер. Однако они верно отражают характер зависимости величин. И еще одно важное замечание: для достоверности результатов, полученных путем анализа статистических данных, этих данных должно быть много.
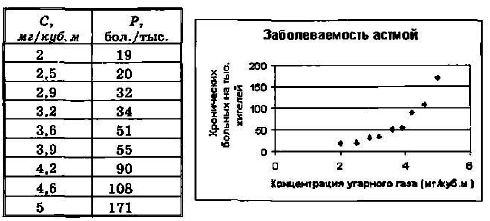
Рис. 2.12. Табличное и графическое представление статистических данных
Из полученных данных можно сделать вывод, что при концентрации угарного газа до 3 мг/куб. м его влияние на заболеваемость астмой несильное. С дальнейшим ростом концентрации наступает резкий рост заболеваемости.
А как построить математическую модель данного явле¬ния? Очевидно, нужно получить формулу, отражающую за¬висимость числа хронических больных Р от концентрации угарного газа С. На языке математики зто называется функ¬цией зависимости Р от С: Р(С). Вид такой функции неизвес¬тен, ее следует искать методом подбора по эксперименталь¬ным данным.
-Понятно нтсл ЛтдоцЬик .искомой 1|*ушкдгаи ^1ЛЛЖЙР луюхр-дить близко к точкам диаграммы экспериментальных дан¬ных* Строить функцию так, чтобы ее график точно прохо¬дил через все данные точки (рис. 2.13 а), не имеет смысла. Во-первых, математический вид такой функции может ока¬заться слишком сложным. Во-вторых, уже говорилось о том, что зксцериментальные значения являются прибли¬женными.
Отсюда следуют основные требования к искомой функ¬ции:
• она должна быть достаточно простой для использования ее в дальнейших вычислениях;
• график этой функции должен проходить вблизи экспери¬ментальных точек так, чтобы отклонения этих точек от графика были минимальны и равномерны (рис. 2.13 б).
Подученную функцию, график которой приведен на рис. 2.13 tf, принято называть в статистике регрессионной моделью.
а) б)
Рис. 2.13. Два варианта построения графической зависимости
по экспериментальным данным
Коротко о главном
Статистика: наука о сборе, измерении и анализе массо¬вых количественных данных.
Статистические данные носят приближенный, усреднен¬ный характер, получаются путем многократных измерений.
Регрессионная модель — это функция, описывающая за¬висимость между количественными характеристиками сложных систем. Вид регрессионной функции определяется путем подбора по экспериментальным данным.
Вопросы и задания
1. а) Что такое статистика?
б) Являются ли результаты статистических расчетов точными?
в) Что такое регрессионная модель?
2. Какие из следующих величин можно назвать статистическими:
температура вашего тела в данный момент, средняя температу-
ра в вашей регионе за последний месяц; максимальная ско-
рость, развиваемая данной моделью автомобиля; среднее число
осадков, выпавших в вашем регионе в течение года.
Семакин И.Г., Хеннер Е.К., Информатика и ИКТ, 11
Отослано читателями из интернет-сайтов
Содержание урока
 конспект урока конспект урока
 опорный каркас опорный каркас
 презентация урока презентация урока
 акселеративные методы акселеративные методы
 интерактивные технологии
Практика интерактивные технологии
Практика
 задачи и упражнения задачи и упражнения
 самопроверка самопроверка
 практикумы, тренинги, кейсы, квесты практикумы, тренинги, кейсы, квесты
 домашние задания домашние задания
 дискуссионные вопросы дискуссионные вопросы
 риторические вопросы от учеников
Иллюстрации риторические вопросы от учеников
Иллюстрации
 аудио-, видеоклипы и мультимедиа аудио-, видеоклипы и мультимедиа
 фотографии, картинки фотографии, картинки
 графики, таблицы, схемы графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты
Дополнения притчи, поговорки, кроссворды, цитаты
Дополнения
 рефераты рефераты
 статьи статьи
 фишки для любознательных фишки для любознательных
 шпаргалки шпаргалки
 учебники основные и дополнительные учебники основные и дополнительные
 словарь терминов словарь терминов
 прочие
Совершенствование учебников и уроков прочие
Совершенствование учебников и уроков
 исправление ошибок в учебнике исправление ошибок в учебнике
 обновление фрагмента в учебнике обновление фрагмента в учебнике
 элементы новаторства на уроке элементы новаторства на уроке
 замена устаревших знаний новыми
Только для учителей замена устаревших знаний новыми
Только для учителей
 идеальные уроки идеальные уроки
 календарный план на год календарный план на год
 методические рекомендации методические рекомендации
 программы программы
 обсуждения
Интегрированные уроки обсуждения
Интегрированные уроки
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.
|











