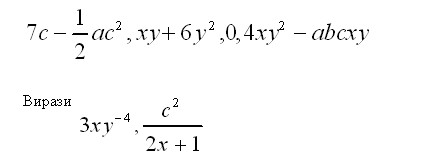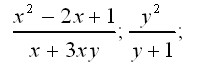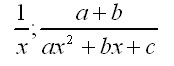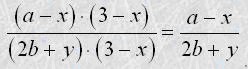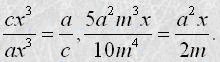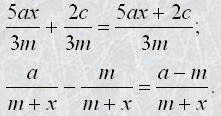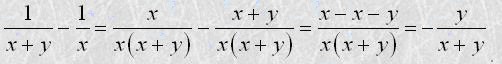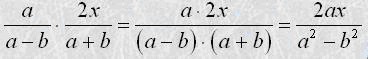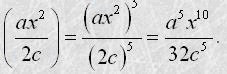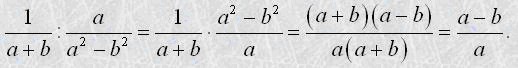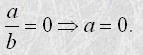Гіпермаркет Знань>>Математика>>Математика 7 клас. Повні уроки>> АЛГЕБРА: Вирази зі змінними. Цілі раціональні вирази.Повні уроки

АЛГЕБРА

Тема 5. Вирази зі змінними. Цілі раціональні вирази

Мета: дізнатися, що таке вирази зі змінними; зрозуміти, які вирази називаються раціональними; навчитися розв’язувати приклади із раціональними виразами.

План: 1. Що таке алгебраїчний вираз? Що таке вирази зі змінними?

           2. Цілі раціональні вирази. Дробові раціональні вирази.

1. Що таке алгебраїчний вираз?Що таке вирази зі змінними?

Якщо з'єднати числа, знаки дій, дужки в одному виразі, то отримаємо числовий вираз. Приклади числових виразів: 1+2 (1 / 2+ 3 / 4) * 15- 8: 2; (3 / 5)- 2 (4 / 5)* 3;

Числовий вираз дорівнює числу, яке ми отримаємо, виконавши всі дії в цьому числовому виразі.

Якщо у виразі крім чисел використовувати букви, то отримаємо буквенний вираз.

Буквеними виразами називають записи, в яких числа і букви з’єднані знаками дій. Наприклад, x-3, x+y, 3a+2b, c:d. Буквений вираз, який показує залежність між величинами, позначеними буквами, називається формулою. Наприклад, позначимо довжину шляху буквою S, швидкість рівномірного руху – буквою V, а час – буквою t. Тоді вираз S=V*t є формулою шляху. Із цієї формули можна виразити інші змінні величини:V=S/t - формула швидкості,t=S/V - формула часу.

Перетворення виразів:

1. При розкритті дужок, перед якими стоїть "+", цей знак і дужки можна опустити. Наприклад, a+(-b+c+4)=a-b+c+4.

2. Щоб розкрити дужки, перед якими стоїть знак "-", слід опустити дужки і знак "-", змінивши знаки всіх доданків у дужках на протилежні. Наприклад, -(a-b)=-a+b; x-(-y+z)=x+y-z.

3. Якщо перед дужками стоїть множник, то на нього умножають кожний доданок у дужках. Наприклад, 6+4(a-b)=6+4a-4b; -4(5-3a)=-20+12a.

Доданки, які мають однакову буквену частину, називають подібними доданками. Наприклад, 4a і (-5a).

Додавання і віднімання подібних доданків називається зведенням подібних доданків. Щоб звести подібні доданки треба додаті їх коефіціенти і результат помножити на їх спільну буквену частину. Наприклад, -4a+6a=(-4+6)a=2a; a-4a+7a=(1-4+7)a=4a.

Якщо доданки мають спільний множник, то його можна винести за дужки. Наприклад,6x+6y=6(x+y); 2ab+b=b(2a+1).

Якщо доданки мають спільний множник, то його можна винести за дужки, а в дужках залишиться сума інших множників. Наприклад, 6a+6b=6(a+b); 2xy+y=y(2x+1).

2. Цілі раціональні вирази. Дробові раціональні вирази

                                                               Цілі раціональні вирази

Цілими раціональними виразами називаються числові вирази, а також вирази із змінними, які можуть містити дії додавання, віднімання, множення, піднесення змінних до натурального степеня. Приклади цілих раціональних виразів:

Вирази не є цілими раціональними, бо містять операції піднесення до від'ємного степеня і ділення на змінні.

                                        Дробові раціональні вирази. Основна властивість раціонального дробу

Дробовими раціональними (дробово-раціональними) виразами називають вирази із змінними, які можуть містити операції додавання, віднімання, множення, піднесення змінних до натурального степеня, а також ділення на вирази із змінними. Приклади дробово-раціональних виразів:

Раціональним дробом називається вираз P/Q , де P і Q – раціональні вирази, причому вираз Q обов'язково містить змінні. Приклади раціональних дробів:

Основна властивість дробу Якщо чисельник і знаменник дробу помножити на один і той самий вираз, то дістанемо дріб, який тотожно дорівнює даному. Наприклад

Основна властивість дробу дає можливість замінити дріб тотожно рівним йому дробом. Таке перетворення називають скороченням дробу (скорочення дробу - reduction of fraction) . Наприклад

Щоб додати дроби з однаковими знаменниками, треба додати їх чисельники, а знаменник залишити той самий. Щоб знайти різницю дробів з однаковими знаменниками, треба від чисельника зменшуваного відняти чисельник від'ємника, а знаменник залишити той самий. Наприклад

Якщо треба знайти суму або різницю дробів з різними знаменниками, то спочатку їх зводять до спільного знаменника. Наприклад

Щоб помножити дріб на дріб, треба перемножити окремо їх чисельники і окремо знаменники і перший добуток записати чисельником, а другий - знаменником дробу. Наприклад

Щоб піднести дріб до степеня, треба піднести до цього степеня чисельник та знаменник і перший результат записати у чисельнику, а другий - у знаменнику дробу. Наприклад

Щоб поділити один дріб на другий, треба перший дріб помножити на дріб, обернений до другого. Наприклад

Значення дробу дорівнює нулю лише, коли чисельник перетворюється на нуль:

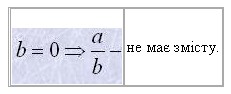
Дріб не має змісту у випадку, коли знаменник перетворюється на нуль:

Вираз, складений з чисел і змінних за допомогою дій додавання, віднімання, множення, ділення і піднесення до степеня, називається раціональним виразом.

Перевір себе:

1. Відомо, що a-b=6; с=5. Знайти значення виразу: 1) a - b+3c; 2) c*(b-a); 3)3/c - 2/a-b.

2. При яких значеннях змінної має сенс вираз: 1) 3х+4; 2) 8/с-5; 3) 1/(1+1/х).

Список використаної літератури:

1. Урок на тему «Вирази зі змінними» викладача Конченко Т. М. , Гімназії міжнародних відносин, м. Київ (СЗШ №323).

2. Урок на тему «Цілі і дробові раціональні вирази» викладача Конченко Т. М. , Гімназії міжнародних відносин, м. Київ (СЗШ №323).

3. Істер О. А. «Алгебра. 7 клас». 4. Мерзляк А. Г., Полонський В. Б., Рабінович Ю. М., ЯкірМ. С. Збірник задач і завдань для тематичного оцінювання з алгебри для 7 класу. – Харків, Гімназія, 2004. – 112 с.: іл.

Відредаговано і надіслано Мазуренко М.С.

Над уроком працювали

Конченко Т. М.

Мазуренко М.С.

Поставить вопрос о современном образовании, выразить идею или решить назревшую проблему Вы можете на Образовательном форуме, где на международном уровне собирается образовательный совет свежей мысли и действия. Создав блог, Вы не только повысите свой статус, как компетентного преподавателя, но и сделаете весомый вклад в развитие школы будущего. Гильдия Лидеров Образования открывает двери для специалистов  высшего ранга и приглашает к сотрудничеству в направлении создания лучших в мире школ.