Гипермаркет знаний>>Математика>>Математика 8 класс. Полные уроки>>Геометрия: Расстояние между точками. Полные уроки

<met akeywords>Гипермаркет знаний, Геометрия, Планиметрия, 8 класс, Расстояние между точками</metakeywords>ТЕМА УРОКА: Расстояние между точками.

Цели урока:

• Углубить знания по геометрии и познакомится с новым материалом для анализирования.
• Познакомиться с новыми определениями и вспомнить некоторые уже изученные.
  
• Научиться применять свойства фигур при решении задач.
• Развивающие – развить внимание учащихся, усидчивость, настойчивость, логическое мышление, математическую речь.
• Воспитательные - посредством урока воспитывать внимательное отношение друг к другу, прививать умение слушать товарищей, взаимовыручке, самостоятельность.

Задачи урока:

• Проверить умение учащихся решать задачи.
• Заинтересовать в геометрии как науке.

План урока:

1. Вступительное слово.
   
2. Повторение ранее изученного материала.
3. Историческая справка.
4. Расстояние между точками.
5. Логические задачи.

Вступительное слово.

В течение почти 2.5 тысячелетий евклидова геометрия является одним из столпов школьной математики. практически в неизменной форме она дошла до нашего времени. Случай этот уникален. почти забыта физика Аристотеля, о математическом анализе Архимеда вспоминают лишь историки математики. Школьная же геометрия базируется на геометрии Евклида. Разница в основном лишь в методике изложения.

Евклид - древнегреческий математик. Мировую известность приобрёл благодаря сочинению по основам математики «Начала» ок. 300 г. до н. э.

Сила   традиционной   геометрии   -   в   ее  общности, универсальности. Слабость  -  в  абстрагировании,  создающем предпосылки для размытия основополагающих понятий геометрии, размытия,   затрудняющего  их   сопоставление  с   реальными объектами,   явлениями  или   процессами.  До  определенного времени   этому  обстоятельству   не  придавали   серьезного значения, однако, когда наступила пора подвергнуть геометрию критическому   переосмысливанию,   высветилась   эта  слабая сторона  геометрии. Возникла  парадоксальная ситуация: самая точная и,  по-видимому, самая наглядная наука  - геометрия - базируется на понятиях,  не поддающихся точным определениям. Чтобы оправдать такое сильное утверждение, полезно напомнить некоторые истины.

Учитель, начиная обучение  геометрии, произносит слова: "Точка  - объект,  лишенный протяженности,  линия -  объект, характеризуемый  длиной,  но  лишенный  ширины"  -  и  затем иллюстрирует эти определения,  отмечая  мелом на доске точку и проводя линию. Однако, размеры такой  точки ~ 1 мм, ширина
линии также  ~ 1 мм  - символ точечности?  Это утверждение в значительной степени базируется на авторитете учителя.

Те  же  трудности  возникают  при  попытках эмпирически воспроизвести  другое  основное  понятие  геометрии - прямую линию.  Обычно полагают,  что эталоном  прямой является  луч света,  распространяющийся в  пустом пространстве.  Однако в соответствии  с  основными  принципами  оптики  и  квантовой механики ширина пучка света  по порядку величины равна длине волны LAM, а это значение невозможно свести к нулю.

Повторение ранее изученного материала.

Файл:O.gif В геометрии, точкой называют абстрактный объект в пространстве, не имеющий ни объёма, ни площади, ни длины, ни каких-либо других измеримых характеристик.

Файл:O.gif Таким образом, точкой называют нульмерный объект.

Файл:O.gif Точка является одним из фундаментальных понятий в математике; любая геометрическая фигура считается состоящей из точек.

С точкой все понятно, но что же подразумевает человек когда говорит "точка в пространстве"?

Мы можем теперь использовать три основные понятия, чтобы дать основные определения.

Пространство - это множество всех точек.

Геометрическая фигура это - любое множество точек, прямых и плоскостей.

Точка, прямая и плоскость являются геометрическими фигурами.

Множество точек называется коллинеарным, если существует прямая, содержащая все эти точки.

Множество точек называется компланарным, если существует плоскость, содержащая все эти точки.

Если точка A расположена на размеченной прямой, которая называется в этом случае "числовая прямая", то число, соответствующее этой точке, называется ее координатой. В дальнейшем, запись A(a) будет обозначать, что координата точки A число a.

Расстояние между точками А(a) и В(b) на прямой - это модуль разности их координат, то есть AB=|(a-b)|.

Историческая справка.

Евклид начинает  "Начала" с определения точки: "Точка есть то, что не имеет частей". Исторические корни  двух названий точки,  можно найти, смотря семантические пучки однокоренных слов, используемых для обозначения точки: здесь и "отпечаток", "след"  и точка.  Например, "stigmh" математическая точка  (Arst), (но: "stigma " наколотая  отметка; "stigmow" - укол, колотая рана). Отсюда понятно, первоначальное понятие точки, как центра . Оно  обозначает колющее орудие, которым в древности погоняли животных в упряжке  (старое русское слово "рожон").

В нашем случае речь идёт об острие ножки циркуля, закреплявшейся при вычер­чивании круга. Этим термином пользовался ещё автор первых  "Элемен­тов"  Гиппократ. .Латинские термины возникают не сразу. У Марциада Капеллы (5 в. н. э.) ещё говорится  "punodum  circult"   (точка круга),  и  "media nota circult" (средняя метка круга).

Расстояние между точками.

В координатах:

Файл:T.gif Теорема. Расстояние между точками A₁ и A₂ можно вычислить по формуле.

 в пространстве:

Файл:81062011 2.gif

на плоскости:

Файл:81062011 3.gif

на прямой:

Файл:81062011 4.gif

Попробуем применить эти формулы на практике и посмотрим что получится.

Пример №1.

Задание:

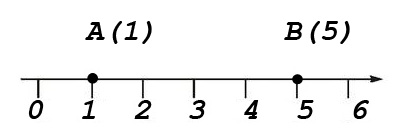
Рассмотрим простейший пример для нахождения расстояния между двумя точками, когда эти точки находятся на прямой. И так у нас есть прямая, на прямой обозначим две точки А и В. Координаты точек равны 2 и 7, соответственно.

Решение:

По формулам: Файл:81062011 6.gif

Ответ: АВ=5

Ответ был очевиден и известен еще до начала решения. Банально, можно было просто посчитать количество единичных отрезков между точками.

Но что делать если точки находятся на плоскости и прямая этих точек не параллельна осям координат.

Пример №2.

Задание:

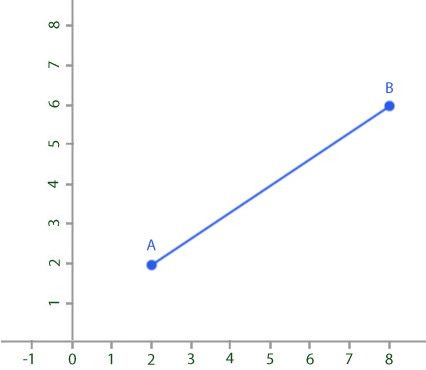
Найти расстояние между точками А и В, если известны их координаты (2;2) и (8;6).

Решение:

Используем формулу для нахождения расстояния на плоскости. Подставляем соответствующие значения, получаем ответ.

Файл:81062011 7.gif

Ответ: АВ=7,211

Для нахождения расстояния мы используем формулы, не обязательно их заучивать, нужно просто их понять. И так в Примере №1 все предельно ясно, но вот в Пример №2 появляется вторая ось и расчеты немного усложняются. Грубо говоря мы находим смещение по каждой из осей(расстояние какое отрезок проходит по каждой из осей), т.е. сначала о оси абсцисс (ОХ) (х2-х1) возносим в квадрат, тоже самое действие проводим для значений по оси ординат (ОУ) (у2-у1) этаже самая манипуляция с квадратом. В конечном итоге суммируем полученные значения и извлекаем корень(корень извлекается потому что ранее значения были возведены в квадрат).

Для внесения полной ясности рассмотрим пример с тремя координатами когда точки находятся в пространстве.

Пример №3.

Задание:

Точка А(2;4;7) точка В(9;4;3).

Найти расстояние между А и В.

Решение:

Файл:81062011 8.gif

Ответ: АВ=8,062

Как видно с уравнения в этом случаи у нас добавилось смещение по оси аппликат (OZ).

Интересный факт:

Эволюция вычислительных средств.

С давних пор люди стремились облегчить вычисления. Самой древней "счётной машиной" были пальцы рук и ног, камешки, раковины и другие мелкие предметы. Ремесленники и торговцы пользовались для счёта доской, разграфлённой на столбцы, на которой с помощью камешков откладывались единицы различных разрядов. Эту доску называли абаком. От римлян к нам пришло слово "калькуляция", что означает буквально "счёт камушками". В настоящее время термин "калькуляция" используется в смысле вычисление. Усовершенствование абака привело к появлению счетов ( в древнем Китае - Суан-чан, в Японии-сорабан). Русские счеты появились в XVI в.

Машину для механического производство арифметических действий называют арифмометром. Одними из первых таких машин были машины, созданные в 1641 году французским учёным Блезом Паскалем (1623 - 1662) и в 1671 году Г.Лейбнцем. Массовое распространение получил арифмометр, сконструированные в 1874 году петербургским механиком В.Однером.

Суммирующая машина Блеза Паскаля

Революцию в вычислительной технике совершили электронные вычислительные машины (ЭВМ), которые появились в середине XX столетия. Первая ЭВМ была создана в США в 1944 году. Первая советская ЭВМ была создана под руководством академика С.А.Лебедева (1902-1974) в 1950 году. Современные ЭВМ производят несколько миллионов операций в секунду и находят широкое применение в различных областях науки и народного хозяйств. Простейшие ЭВМ, получившей широкое распространение в практической деятельности, является микрокалькулятор.

Но есть и множество способов проводить арифметические репарации в уме.

Вопросы:

1. Что такое точка?
2. В каких еще науках используется понятие точки?
3. Какая разница в нахождении расстояния между точками в пространстве и на плоскости?

Список использованных источников:

1. И.Л.Розенталь "Геометрия, динамика, вселенная"
2. Вилофич А. Н., учитель геометрии (9-11 класс), г. Москва, школа №354.
3. Левченко В.С., учитель геометрии.

Над уроком работали:

Потурнак С.А.

Васин Алексей

Поставить вопрос о современном образовании, выразить идею или решить назревшую проблему Вы можете на Образовательном форуме, где на международном уровне собирается образовательный совет свежей мысли и действия. Создав блог, Вы не только повысите свой статус, как компетентного преподавателя, а и сделаете весомый вклад в развитие школы будущего. Гильдия Лидеров Образования открывает двери для специалистов  высшего ранга и приглашает к сотрудничеству в направлении создания лучших в мире школ.