Гипермаркет знаний>>Математика>>Математика 8 класс. Полные уроки>>Геометрия: Уравнение окружности. Полные уроки

ТЕМА УРОКА: Уравнение окружности.

Цели урока:

• Попытаться разобраться как видели геометрию основоположники.
• Познакомиться с новыми определениями и вспомнить некоторые уже изученные.
  
• Сформулировать свойства окружности.
  
• Научиться применять свойства фигур при решении задач.
• Развивающие – развить внимание учащихся, усидчивость, настойчивость, логическое мышление, математическую речь.
• Воспитательные - посредством урока воспитывать внимательное отношение друг к другу, прививать умение слушать товарищей, взаимовыручке, самостоятельность.

Задачи урока:

• Проверить умение учащихся решать задачи.

План урока:

1. Вступительное слово.
   
2. Повторение ранее изученного материала.
3. Уравнение окружности.
   

Вступительное слово.

По традиции начнем с повторения ранее изученного материала. Для того что бы полностью разобраться с уравнением окружности нам нужно вспомнить:

• какие геометрические примитивы существуют
  
• как окружность взаимосвязана с другими примитивами
• что такое прямоугольная система координат
  
• что такое окружность и круг на первый взгляд
  

Вы уверены что знаете, что такое окружность? Окружность- это не только замкнутая линия, но и совершенная линия, так считал Аристотель. А как считают сейчас? Где вы видите окружность? А она... Эллипс - окружность?

Немного истории.

Только в Древней Греции окружность и круг получили свои названия.

Самая простая из всех кривых линий - окружность. Это одна из древнейших геометрических фигур. Философы древности придавали ей большое значение. Согласно Аристотелю, небесная материя, из которой состоят планеты и звезды, как самая совершенная, должна двигаться по самой совершенной линии - окружности. Сотни лет астрономы считали, что планеты двигаются по окружностям. Это ошибочное мнение было опровергнуто лишь в XVII веке учением Коперника, Галилея, Кеплера и Ньютона.

Аристотель, также известный как Стагирит по месту рождения (384, Стагир — 322 до н.э., Халкида на Эвбее) — древнегреческий философ и учёный.

Николай Коперник (1473-1543) — польский астроном, создатель гелиоцентрической системы мира.	Галилео Галилей (итал. Galileo Galilei; 1564-1642) — итальянский физик, механик, астроном, философ и математик, оказавший значительное влияние на науку своего времени.

Иоганн Кеплер (нем. Johannes Kepler; 1571-1630) — немецкий математик, астроном, оптик и астролог. Открыл законы движения планет.	Сэр Исаак Ньютон (англ. Sir Isaac Newton, 1642-1727) — английский физик, математик и астроном, один из создателей классической физики.

Повторение ранее изученного материала.

Круглые тела в древности заинтересовали человека. Так в Древнем Египте для постройки знаменитых египетских пирамид никаких технических сооружений еще не было. Даже шлифовать огромные каменные глыбы приходилось вручную, а перемещали их с помощью бревен круглой формы. Позже вместо бревен стали использовать их части – в виде колес, которые катились уже легче.

Геометрические примитивы.

Фигура – это произвольное множество точек на плоскости. Точка, прямая, отрезок, луч, треугольник, круг, квадрат и так далее – всё это примеры геометрических фигур.

Основными геометрическими фигурами на плоскости являются точка и прямая. Этим фигурам в геометрии не даётся определений.

Неопределяемыми геометрическими фигурами на плоскости являются точка и прямая.

Точки принято обозначать прописными латинскими буквами: А, В, С, D …. Прямые обозначаются строчными латинскими буквами: а, b, с, d ….

Точка — это одно из фундаментальных понятий геометрии, поэтому "точка" не имеет определения. Евклид определил точку как то, что нельзя разделить.
Также в геометрии нет определения "прямой" (имеется в виду прямая линия).

Прямая — одно из основных понятий геометрии.
Геометрическая прямая (прямая линия) — незамкнутый с двух сторон, протяженный не искривляющийся геометрический объект, поперечное сечение которого стремится к нулю, а продольная проекция на плоскость даёт точку.

Файл:O.gif Треугольник — простейший многоугольник, имеющий 3 вершины (угла) и 3 стороны; часть плоскости, ограниченная тремя точками, и тремя отрезками, попарно соединяющими эти точки.

Файл:19102010 8.gif

Файл:O.gif Прямоугольник — это параллелограмм , у которого все углы прямые (равны 90 градусам).

Файл:O.gif Окружность — геометрическое место точек плоскости, равноудалённых от заданной точки, называемой центром, на заданное ненулевое расстояние, называемое её радиусом.

Связь окружности с другими фигурами.

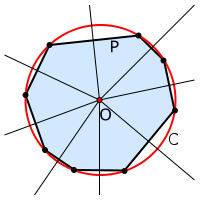
Файл:O.gif Описанная окружность многоугольника — окружность, содержащая все вершины многоугольника. Центром является точка (принято обозначать O) пересечения серединных перпендикуляров к сторонам многоугольника.

Файл:O.gif Окружность называется вписанной в выпуклый многоугольник, если она лежит внутри данного многоугольника и касается всех прямых, проходящих через его стороны.

Прямоугольная система координат.

И так эта система координат имеет два своих вполне оправданных названия. Первым из них является декартова, такое название она получила от фамилии своего автора. И второе не менее интересное и оправданное - прямоугольная система координат, происхождение такого имени становится понятным после первого взгляда на саму систему координат. Угол между двумя направляющими равен 90° такое угол зачастую называют прямым, откуда и пошло второе название.

Окружность и круг.

Файл:O.gif Окружность - это замкнутая прямая линия, все точки которой расположены на одинаковом расстоянии от одной внутренней точки, которая называется центром.

Файл:O.gif А круг - это часть плоскости, ограниченная окружностью.

Файл:13062011 5.gif

Файл:O.gif Диаметр - это отрезок, который соединяет две точки окружности и проходит через центр этой окружности, это максимальное расстояние между точками одной фигуры. А вот половинка диаметра называется радиусом.

Файл:O.gif Радиус соединяет центр окружности с любой точкой окружности. Есть еще такое необычное слово - хорда.

Файл:O.gif Хорда - это отрезок, который соединяет две точки окружности, но, в отличие от диаметра, хорда не проходит через центр окружности - ей больше нравится находиться около окружности.

Файл:O.gif Круговым сектором или просто сектором называется часть круга, ограниченная дугой и двумя радиусами, соединяющими концы дуги с центром круга.

Для построения окружности необходим новый чертежный инструмент – циркуль.

Уравнение окружности.

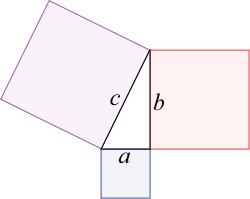
Есть много способов для предоставления уравнения окружности, но как по мне, одним из самых простых это с помощью теоремы Пифагора.

Файл:T.gif теорема Пифагора:

Геометрическая формулировка:

• В прямоугольном треугольнике площадь квадрата, построенного на гипотенузе, равна сумме площадей квадратов, построенных на катетах.
  

Алгебраическая формулировка:

• В прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов.

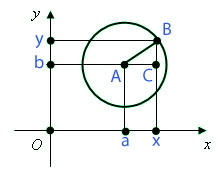
Пусть есть окружность с центром в точке A (a; b) и радиусом R. Возьмем произвольную точку В (x; y) на окружности. Тогда, как видно из рисунка можно применить теорему Пифагора.

Получаем прямоугольный треугольник с сторонами АВ, ВС и СА.

По теореме Пифагора

Файл:13062011 9.gif

Если применить это к нашей окружности получим следующие уравнение

Файл:13062011 7.gif

- это уравнение окружности.

Если центр окружности находится в начале координат, т.е. a=0 и b=0, то уравнение окружности принимает вид:

Обратно: любая точка В, координаты которой удовлетворяет данному уравнению окружности, принадлежат окружности.

Интересный факт:

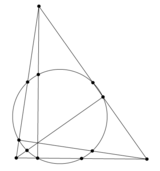
Окружность девяти точек.

В геометрии треугольника окружность девяти точек — это окружность, проходящая через середины всех трёх сторон треугольника. Она также называется окружностью Эйлера, окружностью Фейербаха, окружностью шести точек.

Окружность девяти точек получила такое название из-за следующей теоремы:

Файл:T.gif Основания трёх высот произвольного треугольника, середины трёх его сторон и середины трёх отрезков, соединяющих его вершины с ортоцентром, лежат все на одной окружности.

Окружность девяти точек обладает ещё целым рядом свойств:

• Центр окружности девяти точек лежит на прямой Эйлера, точно в середине отрезка между ортоцентром и центром описанной окружности.
• Радиус окружности девяти точек равен половине радиуса описанной окружности. Более того, описанная окружность есть образ окружности девяти точек относительно гомотетии с центром в ортоцентре и коэффициентом 2.
• (теорема Фейербаха) Окружность девяти точек произвольного треугольника касается вписанной и всех трёх вневписанных окружностей этого треугольника.

Эйлер в 1765 году доказал, что основания высот и середины сторон лежат на одной окружности (отсюда название «окружность шести точек»). Первое полное доказательство общего результата было, по-видимому, опубликовано Карлом Фейербахом в 1821 году (вместе с теоремой, носящей его имя), но есть указания на то, что оно было известно и ранее.

Вопросы:

1. Что такое геометрические примитивы?
   
2. В чем разница между кругом и окружностью?
3. С помощью какой теоремы можно представить уравнение окружности?
   

Список использованных источников:

1. Бубенцова Марина Николаевна, учитель математики МОУ СОШ с. Ульяновка, Тамалинского района
   
2. Понарин Я.П. Элементарная геометрия. В 2 тт.. — М.: МЦНМО, 2004
   
3. Льюис Кэррол, «История с узелками»
   

Над уроком работали:

Потурнак С.А.

Бубенцова Марина Николаевна

Поставить вопрос о современном образовании, выразить идею или решить назревшую проблему Вы можете на Образовательном форуме, где на международном уровне собирается образовательный совет свежей мысли и действия. Создав блог, Вы не только повысите свой статус, как компетентного преподавателя, а и сделаете весомый вклад в развитие школы будущего. Гильдия Лидеров Образования открывает двери для специалистов  высшего ранга и приглашает к сотрудничеству в направлении создания лучших в мире школ.