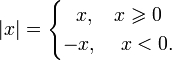Гипермаркет знаний>>Математика>>Математика 6 класс. Полные уроки>>Математика: Модуль числа. Полные уроки

Тема урока

• Модуль числа
  

Тип урока

• изучение и первичное усвоение нового материала

Цели урока

• формирование понятия «модуль», умения находить модуль числа.
• развитие логического мышления, математической речи, сознательного восприятия учебного материала.
• Углубить знания по геометрии, изучить историю происхождения.
• Развивающие – развить внимание учащихся, усидчивость, настойчивость, логическое мышление, математическую речь.
• Воспитательные - посредством урока воспитывать внимательное отношение друг к другу, прививать умение слушать товарищей, взаимовыручке, самостоятельность.

Задачи урока

• узнать, что такое модуль
• научиться использовать это понятие при решении задач
• проверить умение учащихся решать задачи.

План урока

1. Введение.
2. Теоретическая часть
3. Практическая часть.
4. Домашнее задание.
5. Интересные факты
6. Вывод

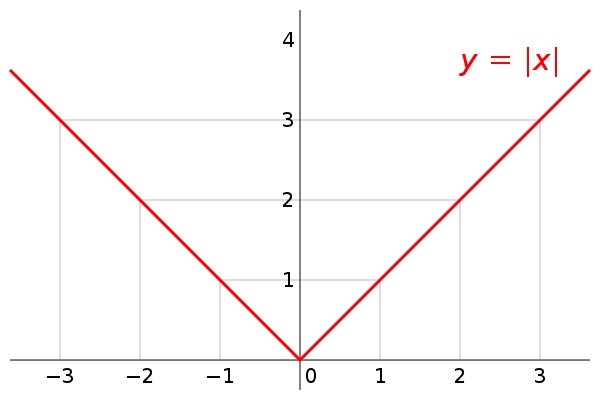
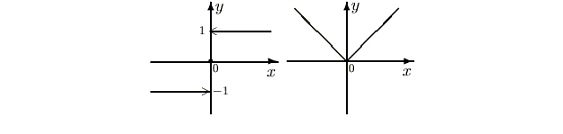
Введение

Сегодня на уроке предстоит сделать немало открытий. Чтобы узнать тему урока, решите ребус.

На рисунке зашифровано слово «модуль». Итак, тема урока – «Модуль числа». В переводе с латинского modulus – «мера». Считают, что термин предложил использовать Котс, ученик Ньютона. Лейбниц тоже использовал эту функцию, которую называл модулем и обозначал: mol x. Общепринятое обозначение абсолютной величины введено в 1841 году Вейерштрассом. Для комплексных чисел это понятие ввели Коши и Арган в начале XIX века.

Теоретическая часть

Определения и основные факты

Как известно, каждое действительное число можно отождествить с точкой на числовой прямой. Поскольку про каждую отличную от нуля точку можно сказать, лежит она левее нуля или правее, а также измерить расстояние от этой точки до нуля, мы можем связать с каждым действительным числом две величины: его знак и его модуль. А именно, если точка, изображающая число х, лежит левее нуля, то говорят, что знак числа х отрицателен, а если правее нуля, то говорят, что знак числа х положителен; число 0 знака не имеет. Модуль числа х, равный расстоянию от точки, изображающей число х, до нуля можно измерить для всех действительных чисел. Например, число 3 положительно, а его модуль равен 3, число -5 отрицательно, а его модуль равен 5; модуль нуля равен нулю. Как мы видим, модуль положительного числа равен самому этому числа. Модуль отрицательного числа равен "минус"-этому числу, то есть противоположному числу; например, модуль числа -5 равен –(–5)=5. Таким образом, каждое действительно число х можно записать в виде х =знак х модуль х.

Например: Расстояние до точки М (-6) от начала отсчета O равно 6 единичным отрезкам. Число 6 называют модулем числа -6. Пишут: |-6| = 6.

Модулем числа а называют расстояние (в единичных отрезках) от начала координат до точки А (а).

Модуль числа 5 равен 5, так как точка В (5) удалена от начала отсчета на 5 единичных отрезков. Пишут: |5| = 5. Модуль числа 0 равен 0, так как точка с координатой 0 совпадает с началом отсчета O, т.е. удалена от нее на 0 единичных отрезков (см. рис. 63). Пишут: |0| = 0. Модуль числа не может быть отрицательным. Для положительного числа и нуля он равен самому числу, а для отрицательного — противоположному числу. Противоположные числа имеют равные модули: |-а| = |а|.

Например,

Итак, абсолю́тная величина́ или мо́дуль, обозначается |x|. В случае вещественного аргумента — непрерывная кусочно-линейная функция, определённая следующим образом:

Обобщением этого понятия является модуль комплексного числа , также иногда называемый абсолютной величиной. Он определяется по формуле:

Свойства модуля

Следующие свойства справедливы для всех действительных значений входящих в них переменных.

1) , причем |a|=0 тогда и только тогда, когда a=0.

2) |-a|=|a|

3) |ab|=|a||b|; в частности, |a|²=|a²|=a².

4)

5) .

6) |a|=max{a, -a}; в частности 

7)

Видео:

Практическая часть

Пример 1.1

Решить уравнение |x²+|-x||=0.

• РЕШЕНИЕ. Преобразуем левую часть уравнения: |x²+|-x||=x²+|x|. Поскольку каждое из полученных слагаемых неотрицательно при всех значениях x, рассматриваемая сумма также всегда неотрицательно, причем равна нулю тогда и только тогда, когда каждое из слагаемых равно нулю. Таким образом, исходное уравнение равносильно уравнению x=0.
• ОТВЕТ: x=0.

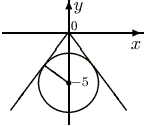
Графики функций – х и |х| выглядят следующим образом. Функция – х разрывна в нуле и нечетна. Функция |х| непрерывна на всей числовой прямой и четна. При отрицательных значениях переменной она убывает? а при положительных - возрастает.

Пример 1.2

При каждом значении параметра a найти число точек пересечения кривых y=a|x| и x²+(y+5)²=9.

• РЕШЕНИЕ. Изобразим на плоскости O_xy данные кривые. Первая из них получается с помощью сжатия и, быть может, симметрии относительно оси O_y графика функции y=|x|, а второе уравнение задает окружность радиуса 3 с центром в точке (0;-5). При a>=0 кривая y=a|x| лежит в первой и второй четвертях включая ось O_x (при a=0 кривая y=a|x| совпадает с осью O_x), а окружность x²+(y+5)²=9 - в третьей и четвертой, не имея общих точек с осью O_x. Следовательно, в этом случае данные кривые не пересекаются.

Пусть теперь a<0. При малых по модулю значениях параметра a у рассматриваемых кривых общих точек по-прежнему не будет. Затем при уменьшении параметра a, произойдет касание (этот момент изображен на рисунке),

а при всех меньших значениях этого параметра будет ровно четыре общие точки. Остается лишь найти то значение параметра a, при котором произойдет касание. Проведя радиус, получим египетский треугольник (то есть треугольник со сторонами 3, 4, 5), из которого нетрудно найти угловой коэффициент соответствующей полупрямой: 4/3 .

• ОТВЕТ: При a<–4/3 число точек пересечения равно четырем, при a=–4/3 - двум, а при a>–4/3 точки пересечения отсутствуют.

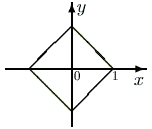
Пример 1.3

Какая геометрическая фигура задается уравнением |x|+|y|=1. Сделать чертеж.

• РЕШЕНИЕ. Нетрудно видеть, что вместе с каждой своей точкой (x, y) наша фигура содержит также точки (– x, y), (x, – y), (– x, – y). Значит, нам достаточно изобразить часть этой фигуры, лежащую в первой четверти, а затем отразить полученную кривую относительно обеих осей и начала координат.

Итак, пусть x>=0 и y>=0. Тогда исходное уравнение принимает вид x+y=1. Значит, лежащей в первой четверти частью фигуры является соответствующий отрезок прямой y=1 – x. Произведя все указанные отражения этого отрезка, получим четырехугольник с равными перпендикулярными диагоналями, то есть квадрат.

• ОТВЕТ: квадрат.

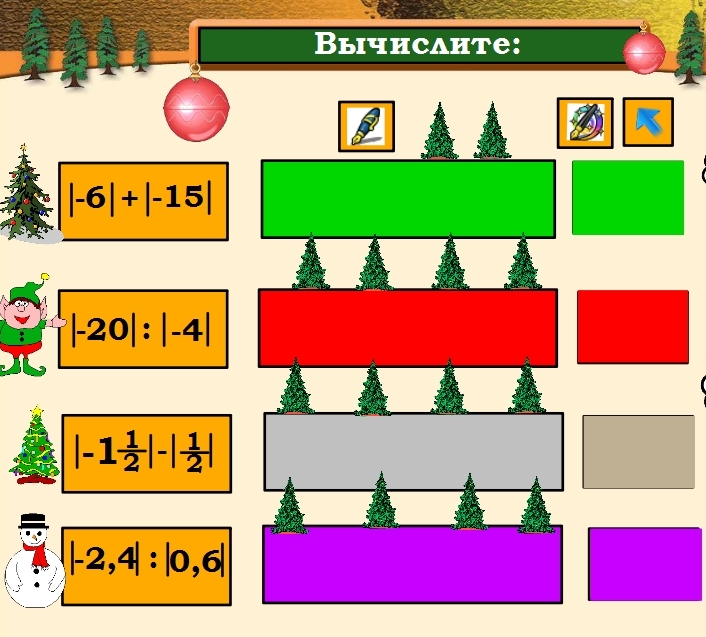
Тест «Модуль числа»

Вариант 1

1. Найдите значение выражения |х|, если х = – 2,5.

А) – 2,5 и 2,5;
Б) 2,5;
С) – 2,5

2. Вставьте вместо точек нужные по смыслу слова: «Модуль отрицательного числа есть число … »

А) ему противоположное;
В) нуль;
С) отрицательное.

3. Выберите верные равенства:1) |– 5| = 5; 2) |– 3| = – 3; 3) |4| = 4.

А) 1;
В) 1 и 2;
С) 2 и 3;
D) 1 и 3;
Е) Все.

4. Известно, что |– а| = 16. Чему равен |а|?

А) – 16;
В) 16 и – 16;
С) 16.

5. Из чисел: 1) – 5,8; 2) 3/7; 3) 0; 4) – 7,35 выберите то, у которого бoльший модуль

А) 4;
В) 3;
С) 2;
D) 1.

6. При каких значениях х верно равенство |х| = 5?

А) – 5 и 5;
В) 5;
С) – 5;
D) Таких чисел нет.

7. Укажите верные неравенства: 1) |– 50| < |30|; 2) |1,5| > |– 0,9|; 3) |13| < |– 13|.

А) 1;
В) 3;
С) 1 и 3;
D) 2;
Е) Все.

8. Найдите расстояние от точки А (– 35, 8) до начала отсчёта.

А) 35,8;
В) 38,5 и – 38,5;
С) 0;

D) – 3,5.

Вариант 2

1.Найдите значение выражения |х|, если х = – 4,3.

А) 4,3;
Б) – 4,3;
С) 4,3 и – 4,3.

2. Вставьте вместо точек нужные по смыслу слова: «Модуль положительного числа есть число … »

А) само это число;
В) отрицательное;
С) нуль.

3. Выберите верные равенства:1) |– 9| = – 9; 2) |– 6| = 6; 3) |– 7| = 7.

А) 2 и 3;
В) 1 и 2;
С) 1 и 3;
D) 3;
Е) Все.

4. Известно, что |– b| = 10. Чему равен |b|?

А) 10;
В) – 10 и 10;
С) – 10.

5. Из чисел:1) – 6,8; 2) 13/7 3) 10;  4) – 11, 5 выберите то, у которого бoльший модуль.

А) 4;
В) 2;
С) 1;
D) 3.

6. При каких значениях х верно равенство | х | = 6?

А) 6;
В) – 6;
С) – 6 и 6;
D) Таких чисел нет.

7. Укажите верные неравенства: 1) |– 60| < |40|; 2) |1,2| > |– 0,12|; 3) |– 15| > |– 15|.

А) 1;
В) 2;
С) 3;
D) 1 и 2;
Е) Все.

8. Найдите расстояние от точки В (– 102,5) до начала отсчёта.

А) 0;
В) – 102,5;
С) 102,5;
D) 102,5 и – 102,5.

Домашнее задание

1. Упростить выражение , если a < 0.
2. Вычислить .

Интересные факты

Поскольку функция «модуль числа» вычисляется достаточно просто (только сравнениями и присваиванием), то обычно она входит в стандартный список функций во все языки программирования. Например, в Pascal есть функция abs(x), а в C fabs(x) для вещественного типа.

Вывод

Модулем неотрицательного действительного числа х называют само это число:

                                                              |х| = х

Модулем отрицательного действительного числа х называют противоположное число:

                                                             |х| = - х

Это записывают так:

Список использованных источников:
1. Математическая энциклопедия (в 5 томах). — М.: Советская Энциклопедия, 2002. — Т. 1.
2. «Новейший справочник школьника» «ДОМ XXI век» 2008 г.
3. Конспект урока на тему "Модуль числа" Автор: Петрова В. П., учитель математики (5-9 класс), г. Киев

Над уроком работали:
Паутинка А.В.
Петрова В.П.

Скомпоновано и отредактировано Паутинкой А.В.

Поставить вопрос о современном образовании, выразить идею или решить назревшую проблему Вы можете на Образовательном форуме, где на международном уровне собирается образовательный совет свежей мысли и действия. Создав блог, Вы не только повысите свой статус, как компетентного преподавателя, а и сделаете весомый вклад в развитие школы будущего. Гильдия Лидеров Образования открывает двери для специалистов  высшего ранга и приглашает к сотрудничеству в направлении создания лучших в мире школ.