Гипермаркет знаний>>Информатика>>Информатика 10 класс>>Информатика: Представление числовой информации с помощью систем счисления

Представление числовой информации с помощью систем счисления

Для записи информации о количестве объектов используются числа. Числа записываются с использованием особых знаковых систем, которые называются системами счисления. Алфавит системы счисления состоит из символов, которые называются цифрами.

Система счисления — это знаковая система, в которой числа записываются по определенным правилам с помощью символов некоторого алфавита, называемых цифрами. Все системы счисления делятся на две большие группы: позиционные и непозиционные. В позиционных системах счисления количественное значение цифры зависит от ее положения в числе, а в непозиционных — не зависит.

Непозиционные системы счисления.

Примером непозиционной системы, которая сохранилась до наших дней, может служить римская система счисления, которая начала применяться более двух с половиной тысяч лет назад в Древнем Риме. В основе римской системы счисления лежат знаки I (один палец) для числа 1, V (раскрытая ладонь) для числа 5, X (две сложенные ладони) для числа 10, а для обозначения чисел 50, 100, 500 и 1000 используются латинские буквы L, С, D и М. В римской системе счисления количественное значение цифры не зависит от ее положения в числе. Например, в римском числе XXX (30) цифра X встречается трижды и в каждом случае обозначает одну и ту же величину — число 10, три раза по 10 в сумме дают 30.

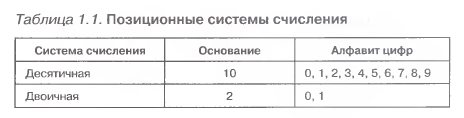
Позиционные системы счисления.

Каждая позиционная система счисления имеет определенный алфавит цифр и основание. Основание системы равно количеству цифр (знаков) в ее алфавите. В позиционных системах счисления количественное значение цифры зависит от ее позиции в числе. Позиция цифры в числе называется разрядом. Разряды числа возрастают справа налево, от младших разрядов к старшим. Основание показывает, во сколько раз изменяется значение цифры при перемещении ее в соседний разряд. В настоящее время наиболее распространенными позиционными системами счисления являются десятичная и двоичная. 

Десятичная система счисления имеет алфавит цифр, который состоит из десяти всем известных, так называемых арабских, цифр {0,1,2,3,4,5,6,7,8,9}, а двоичная — две цифры {0,1} (табл. 1.1).

Десятичная система счисления. В десятичной системе счисления цифра в крайней справа позиции обозначает единицы, цифра, смещенная на одну позицию влево, обозначает десятки, еще левее — сотни, затем — тысячи и т. д.

Рассмотрим в качестве примера десятичное число 333. Цифра 3 встречается в числе трижды, причем самая правая обозначает три единицы, вторая справа — три десятка и, наконец, третья — три сотни. Выше десятичное число 333 было записано в привычной для нас свернутой форме. Мы настолько привыкли к такой форме записи, что уже не замечаем, как в уме умножаем цифры числа на различные степени числа 10, которое является основанием десятичной системы счисления.

В развернутой форме записи числа умножение цифр числа на основание производится в явной форме. Так, в развернутой форме запись числа 333 в десятичной системе будет выглядеть следующим образом: 33310 - 3 • 102 + 3 • 101 + 3 • 100. Для записи десятичных дробей используются разряды с отрицательными значениями степеней основания. Например, число 333,33 в развернутой форме будет записываться следующим образом:

333,33₁₀ = 3 • 10² + 3 • 10¹ + 3 • 10⁰+ 3• 10^-1 + 3 • 10^-2.

Числа в позиционных системах счисления записываются в виде суммы числового ряда степеней основания, в качестве коэффициентов которых выступают цифры данного числа. Умножение или деление десятичного числа на 10 (величину основания) приводит к перемещению запятой, отделяющей

целую часть от дробной, на один разряд вправо или влево. Например:

333,33₁₀ • 10 = 3333,3₁₀,

333,33₁₀ • 10 = 33,333₁₀.

Двоичная система счисления.

Числа в двоичной системе в развернутой форме записываются в виде суммы ряда степеней основания 2 с коэффициентами, в качестве которых выступают цифры 0 или 1. Например, развернутая запись двоичного числа выглядит следующим образом:

А2 = 1 • 2² + 1 • 2¹ + 0 • 2⁰ + 0 • 2^-1 + 1 • 2^-2, а в свернутой форме: А₂ = 110,01₂. Умножение или деление двоичного числа на 2 (величину основания) приводит к перемещению запятой, отделяющей целую часть от дробной на один разряд вправо или влево. Например:

110,01₂ • 2 = 1100,1₂,

110,01₂ : 2 = 11,001₂.

Контрольные вопросы

1. Чем отличаются позиционные системы счисления от непозиционных?

2. Каково основание десятичной системы счисления? Двоичной системы счисления?

3. Какие цифры входят в алфавит десятичной системы счисления? Двоичиой системы счисления?

4. На какую величину в позиционных системах счисления различаются цифры соседних разрядов числа?

Информатика и ИКТ: Учебник для 10 кл. Н.Д. Угринович

Содержание урока
 конспект урока                       
 опорный каркас  
 презентация урока
 акселеративные методы 
 интерактивные технологии 

Практика
 задачи и упражнения 
 самопроверка
 практикумы, тренинги, кейсы, квесты
 домашние задания
 дискуссионные вопросы
 риторические вопросы от учеников

Иллюстрации
 аудио-, видеоклипы и мультимедиа 
 фотографии, картинки 
 графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты

Дополнения
 рефераты
 статьи 
 фишки для любознательных 
 шпаргалки 
 учебники основные и дополнительные
 словарь терминов                          
 прочие 

Совершенствование учебников и уроков
 исправление ошибок в учебнике
 обновление фрагмента в учебнике 
 элементы новаторства на уроке 
 замена устаревших знаний новыми 

Только для учителей
 идеальные уроки 
 календарный план на год  
 методические рекомендации  
 программы
 обсуждения


Интегрированные уроки

Если у вас есть исправления или предложения к данному уроку, напишите нам.

Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.