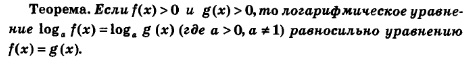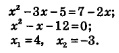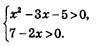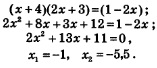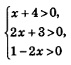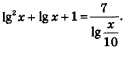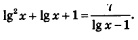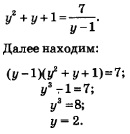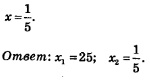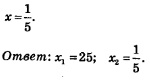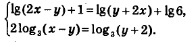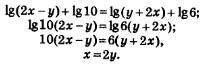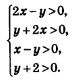Гипермаркет знаний>>Математика>>Математика 10 класс>> Логарифмические уравнения

§ 51. Логарифмические уравнения

Логарифмическими уравнениями называют уравнения вида

где а — положительное число, отличное от 1, и уравнения, сводящиеся к этому виду.
Опираясь на теорему 4 из § 50, согласно которой равенство

справедливо тогда и только тогда, когда 1=8, мы можем сформулировать следующее утверждение.

На практике эту теорему применяют так: переходят от уравнения (1) к уравнению f(х) = g(х) (такой переход называют потенцированием), решают уравнение f(х)= g(х), а затем проверяют его корни по условиям f(х) >0, g(х) >0, определяющим область допустимых значений переменной (ОДЗ). Те корни уравнения f(х) = g(х), которые удовлетворяют этим условиям, являются корнями уравнения (1). Те корни уравнения f(х) =g(х), которые не удовлетворяют хотя бы одному из этих условий, объявляются посторонними корнями для уравнения (1).

Пример 1. Решить уравнение:

Решение.1) Потенцируя (т.е. освободившись от знаков логарифмов), получаем:

2) Проверим наиденные корни по условиям:

Значение x = 4 не удовлетворяет этой системе неравенств (достаточно заметить, что x = 4 не удовлетворяет второму неравенству системы), т.е. x = 4 — посторонний корень для заданного уравнения. Значение x =-3 удовлетворяет обоим неравенствам системы, а потому х = —3 — корень заданного уравнения.

Ответ: х = -3.

Пример 2. Решить уравнение:

Решение. 1) Сначала надо преобразовать уравнение к виду (1). Для этого воспользуемся правилом: «сумма логарифмов равна логарифму произведения». Оно позволяет заменить выражение log₂(х + 4)+ log₂(2x + 3) выражением log²(х + 4)(2x: + 3). Тогда заданное уравнение можно переписать в виде:

2) Потенцируя, получаем:

3) Проверим найденные корни по условиям:

(обратите внимание: условия для проверки всегда определяют по заданному уравнению). Значение x = -1 удовлетворяет этой системе неравенств, а значение х = -5,5 не удовлетворяет (это посторонний корень).
Ответ: х = -1.

Замечание. Иногда удобнее использовать другой порядок ходов: сначала решить систему неравенств — в примере 2 решением системы неравенств будет интервал (-1,5, 0,5); это — область допустимых значений переменной (ОДЗ) или область определения уравнения. Затем найти корни x₁ = -1, х₂ = -5,5. И, наконец, сделать проверку найденных значений х, но уже не с помощью системы неравенств, а по найденной заранее области допустимых значений. В примере 2 значение x = -1 принадлежит интервалу (-1,5, 0,5), а значение x = -5,5 этому интервалу не принадлежит. Следовательно, х = -5,5 — посторонний корень, т.е. x = -1 — единственный корень заданного логарифмического уравнения.

Пример 3. Решить уравнение:

Решение.

Так как

то заданное уравнение можно переписать в виде

Есть смысл ввести новую переменную y = lg х; тогда уравнение примет вид

Это значение удовлетворяет условию (посмотрите: у записанного выше рационального относительно у уравнения переменная содержится в знаменателе, а потому следует проверить, не обращается ли знаменатель в 0 при найденном значении переменной у).

Итак, у = 2. Но у = lg х, значит, нам осталось решить простейшее логарифмическое уравнение lg х = 2, откуда находим х = 100.

Ответ: х = 100.

Подведем некоторые итоги. Можно выделить три основных метода решения логарифмических уравнений.
1) Функционально-графический метод. Он основан на использовании графических иллюстраций или каких-либо свойств функций. Мы применяли этот метод в § 49.

2)Методпотенцирования.  Он основан на теореме, полученной в начале параграфа. Мы применили этот метод в примерах 1 и 2.

3)    Метод введения новой переменной. Мы применили этот метод в примере 3.

Завершая параграф, рассмотрим пример, в котором для решения уравнения используется еще один метод — метод логарифмирования, и пример решения системы логарифмических уравнений.

Пример 4. Решить уравнение

Решение. Возьмем от обеих частей уравнения логарифмы по основанию 5; зто — равносильное преобразование уравнения, поскольку обе его части принимают только положительные значения. Получим:

позволит переписать заданное уравнение в виде: (l - log₅x) ■ log₅ х = -2. Замечаем, что «проявилась» новая переменная у = log₅ х, относительно которой уравнение принимает весьма простой вид: (1 - у)у = -2. Далее получаем:

Но у = log₅ х, значит, нам осталось решить два уравнения:

log₅ x=2, log₅ x=-1. Из первого уравнения находим х = 5', т.е. х = 25; из второго уравнения находим x =5 , т.е.

Пример 5. Решить систему уравнений

Решение. 1) Преобразуем первое уравнение системы к более простому виду:

2)    Преобразуем второе уравнение системы к более простому виду:

3)    Решим полученную систему уравнений:

Подставив 2у вместо х во второе уравнение, получим

Соответственно из соотношения х = 2у находим х₂ = 4, х₂ = -2. 4) Осталось сделать проверку найденных пар (4; 2) и (-2; -1) с помощью условий, которые мы определяем, анализируя исходную систему уравнений:

Пара (4; 2) удовлетворяет этим условиям, а пара (-2; -1) не удовлетворяет (например, она «не проходит» уже через первое условие 2х -у> 0).

Ответ: (4; 2).

А.Г. Мордкович Алгебра 10 класс

_{Видео по математике скачать, домашнее задание, учителям и школьникам на помощь онлайн}

Содержание урока
 конспект урока                       
 опорный каркас  
 презентация урока
 акселеративные методы 
 интерактивные технологии 

Практика
 задачи и упражнения 
 самопроверка
 практикумы, тренинги, кейсы, квесты
 домашние задания
 дискуссионные вопросы
 риторические вопросы от учеников

Иллюстрации
 аудио-, видеоклипы и мультимедиа 
 фотографии, картинки 
 графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты

Дополнения
 рефераты
 статьи 
 фишки для любознательных 
 шпаргалки 
 учебники основные и дополнительные
 словарь терминов                          
 прочие 

Совершенствование учебников и уроков
 исправление ошибок в учебнике
 обновление фрагмента в учебнике 
 элементы новаторства на уроке 
 замена устаревших знаний новыми 

Только для учителей
 идеальные уроки 
 календарный план на год  
 методические рекомендации  
 программы
 обсуждения


Интегрированные уроки

Если у вас есть исправления или предложения к данному уроку, напишите нам.

Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.