Гипермаркет знаний>>Математика>>Математика 11 класс>>Математика:Объем призмы

Объем призмы

Рассмотрим сначала треугольную призму (рис. 478). Дополним ее до параллелепипеда, как указано на рисунке. Точка О является центром симметрии параллелепипеда. Поэтому достроенная призма симметрична исходной относительно точки О, следовательно, имеет объем, равный объему исходной призмы. Таким образом, объем построенного параллелепипеда равен удвоенному'объему данной призмы.

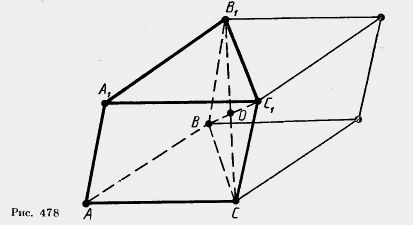
Объем параллелепипеда равен произведению площади его основания на высоту. Площадь его основания равна удвоенной площади треугольника ABC, а высота равна высоте исходной призмы. Отсюда заключаем, что объем исходной призмы равен произведению площади ее основания на высоту.
 

 
Рассмотрим теперь произвольную призму (рис. 479). Разобьем ее основание на треугольники. Пусть — один из этих треугольников. Проведем через произвольную точку X треугольника прямую, параллельную боковым ребрам. Пусть а, — отрезок этой прямой, принадлежащий призме. Когда точка X описывает треугольник , отрезки а, заполняют треугольную призму. Построив такую призму для каждого треугольника , мы получим разбиение данной призмы на треугольные. Все эти призмы имеют одну и ту же высоту, равную высоте исходной призмы.

Объем данной призмы равен сумме объемов треугольных призм, ее составляющих. По доказанному объем треугольной призмы равен произведению площади ее основания на высоту. Отсюда следует, что объем исходной призмы равен:

V=S₁H+S₂H+... + S_nH=(S₁+S₂ + ... + S_n)H,

где S₁, S₂, S_n —площади треугольников, на которые разбито основание призмы, а H — высота призмы. Сумма площадей треугольников равна площади S основания данной призмы. Поэтому

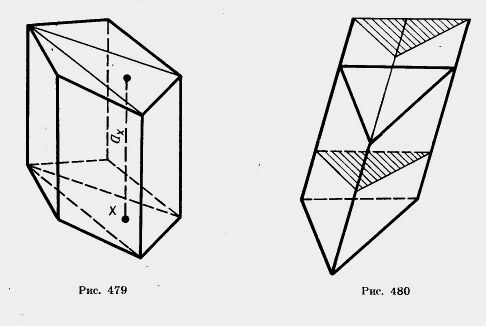
V=SH.

Итак, обтъем любой призмы равен произведению площади ее основания на высоту.

Задача (24). В наклонной призме проведено сечение, перпендикулярное боковым ребрам и пересекающее все боковые ребра. Найдите объем призмы, если площадь сечения Q, а боковые ребра равны I.

Решение. Плоскость проведенного сечения разбивает призму на две части (рис. 480). Подвергнем одну из них параллельному переносу, совмещающему основания призмы. При этом получим прямую призму, у которой основанием служит сечение исходной призмы, а высота равна I. Эта призма имеет тот же объем. Таким образом, объем исходной призмы равен QI.

А. В. Погорелов, Геометрия для 7-11 классов, Учебник для общеобразовательных учреждений

_{Видео по математике скачать, домашнее задание, учителям и школьникам на помощь онлайн}

Содержание урока
 конспект урока                       
 опорный каркас  
 презентация урока
 акселеративные методы 
 интерактивные технологии 

Практика
 задачи и упражнения 
 самопроверка
 практикумы, тренинги, кейсы, квесты
 домашние задания
 дискуссионные вопросы
 риторические вопросы от учеников

Иллюстрации
 аудио-, видеоклипы и мультимедиа 
 фотографии, картинки 
 графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты

Дополнения
 рефераты
 статьи 
 фишки для любознательных 
 шпаргалки 
 учебники основные и дополнительные
 словарь терминов                          
 прочие 

Совершенствование учебников и уроков
 исправление ошибок в учебнике
 обновление фрагмента в учебнике 
 элементы новаторства на уроке 
 замена устаревших знаний новыми 

Только для учителей
 идеальные уроки 
 календарный план на год  
 методические рекомендации  
 программы
 обсуждения


Интегрированные уроки

Если у вас есть исправления или предложения к данному уроку, напишите нам.

Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.