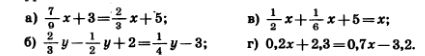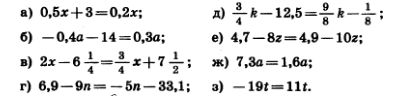Гипермаркет знаний>>Математика>>Математика 6 класс>>Математика: Решение уравнений

Решение уравнений

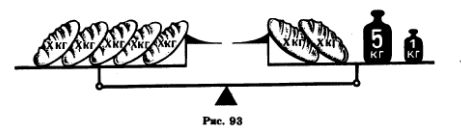
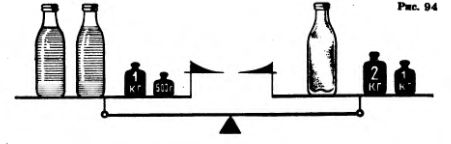
Пример 1. Решим уравнение 4•(x + 5) = 12.

Решение. По правилу отыскания неизвестного множителя имеем х+5 = 12:4, т. е. х + 5 = 3. Это же уравнение можно получить, разделив обе части данного уравнения на 4 или умножив обе части на . Теперь легко найти значение х. Имеем x = 3 — 5, или х = —2.\

Число -2 является корнем уравнения х + 5 = 3 и уравнения 4-(x+5)=12, так как -2 + 5 = 3 и 4-(-2 + 5)=12.

Корни уравнения не изменяются, если его обе части умножить или разделить на одно и то же число, не равное нулю.

Пример 2. Решим уравнение 2х+5 = 17.

Решение. По правилу отыскания неизвестного слагаемого имеем 2х= 17 — 5, т. е. 2x=12. Уравнения 2x + 5 = 17 и 2х= 17—5 имеют один и тот же корень 6, так как 2-6 + 5 = 17 и 2*6 = 17- 5.

Уравнение 2х = 17 — 5 можно записать так: 2х = 17 + (— 5). Видим, что корень уравнения 2x+ 5 =.17 не изменяется, если перенести слагаемое 5 из левой части уравнения в правую, изменив его знак на противоположный.

Пример 3. Решим уравнение 5х = 2х + 6 (рис. 93).

Решение. Вычтем из обеих частей уравнения по 2х (снимем с обеих чашек весов по две буханки хлеба). Получим 5х — 2х = 2х — 2x + 6. Но 2х — 2х = 0, значит, 5х — 2х = 6. Это уравнение можно получить из данного, если слагаемое 2х перенести из правой части в левую, изменив его знак на противоположный. Решая дальше уравнение 5х — 2х = 6, получим 3x = 6 и х=2.

Число 2 есть корень уравнения 5х—2х=6 и уравнения 5x = 2x + 6, так как 5*2 — 2*2 = 6 и 5*2 = 2*2 + 6.

Корни уравнения не изменяются, если какое-нибудь слагаемое перенести из одной части уравнения в другую, изменив при этом его знак.

Пример 4. Решим уравнение
Решение. Умножим левую и правую части уравнения на 3 для того, чтобы освободиться от дробного коэффициента. Получим х + 36 = 3x. Перенесем с противоположными знаками слагаемое 36 из левой части в правую, а слагаемое Зх из правой части в левую: х — 3х= — 36. Упростим левую часть уравнения: — 2х= — 36. Теперь разделим обе части уравнения на —2, получим x = 18.
Число 18 является корнем данного уравнения так как верно равенство .

Во всех рассмотренных примерах мы приводили данные уравнения к виду ах=b, где а0.
Уравнение, которое можно привести к такому виду с помощью переноса слагаемых и приведения подобных слагаемых, называют линейным уравнениемс одним неизвестным.

Обе части уравнения умножили на число, не равное 0. Изменились ли корни данного уравнения? Обе части уравнения разделили на одно и то же число, отличное от нуля. Изменились ли корни данного уравнения? Сформулируйте правило переноса слагаемых из одной части уравнения в другую. Какие уравнения называют линейными?

1298. Перенесите из левой части уравнения в правую то слагаемое, которое не содержит неизвестного:

а) 8x + 5,9 = 7x + 20; б) 6x — 8= —5х—1,6.

1299.    Соберите в левой части уравнения все слагаемые, содержащие неизвестное, а в правой — не содержащие неизвестное:

a) 15y —8= —6y + 4,6; б) — 16z +1,7 = 2z — 1.

1300.    Решите уравнение:

а)    6x -12 = 5х + 4;    д) 4 + 25у = 6 + 24у;
б)    —9a + 8=—10а —2; е) 11 — 5z = 12 — 6z;
в)    7m +1 = 8m + 9;    ж) 4k + 7= — 3 + 5k;
г)    —12n —3 = 11n —3;    з) 6 —2с = 8 —Зс.

Уравнения вида — 7у + 9 = — 8у— 3 читают так: — сумма минус семи игрек и девяти равна сумме минус восьми игрек и минус трех. Корень этого уравнения — число минус двенадцать.

1301.    С помощью умножения обеих частей уравнения на одно и то же число освободитесь от дробных чисел и решите уравнение:

1302.    Решите уравнение и выполните проверку:

а)    —40*( — 7x+ 5)= —1600; в) 2,1*(4-6у)=-42;
б)    (-20*-50)*2 = 100;    г) -3 * (2-15x)=-6.

1303.    Найдите корень уравнения:

1304.    Решите уравнение, используя основное свойство пропорции:

1305.    В первом бидоне в 3 раза больше молока, чем во втором. Если из первого перелить 20 л во второй, то молока в бидонах будет поровну. Сколько молока было в каждом бидоне?

1306.    Длина отрезка АВ на 2 см больше, чем длина отрезка CD. Если длину отрезка АВ увеличить на 10 см, а длину отрезка CD увеличить в 3 раза, то получатся равные результаты. Найдите длину отрезка АВ.

1307.    Автобус проходит расстояние от города до села за 1,8 ч, а легковая автомашина — за 0,8 ч. Найдите скорость автобуса, если известно, что она меньше скорости легковой автомашины на 50 км/ч.

1308.    На первую автомашину погрузили на 0,6 т зерна больше, чем на вторую. Если бы на первую автомашину погрузили в 1,2 раза больше, а на вторую в 1,4 раза больше, то груза на обеих автомашинах было бы поровну. Сколько тонн груза погрузили на каждую автомашину?
1309.    Мама получила премию. На покупку пальто было израсходовано — всей премии, а на покупку туфель премии и еще осталось 75 р. Какую премию получила мама?
1310.    Мебельный гарнитур состоял из стенки, дивана и стола со стульями. Стоимость стенки составляла стоимости всего гарнитура, а стоимость дивана стоимости стенки. Стол со стульями стоил 160 р. Сколько стоил весь гарнитур?
1311.    Три завода получили заказ на изготовление моторов. Первый завод выполнил 0,56 всего заказа, второй того, что выполнил первый завод, а третий завод изготовил остальные 240 моторов. Сколько всего моторов изготовили все три завода?

1312.    Веревку длиной 63 м разрезали на два куска так, что 0,4 длины первого куска были равны 0,3 длины второго куска. Найдите длину каждого куска веревки.

1313.    За 2,5 кг конфет было заплачено 5,5 р. Сколько денег надо доплатить, чтобы купить 2,9 кг таких конфет?

1314.    В растворе содержится 40% соли. Если добавить 120 г соли, то в растворе будет содержаться 70% соли. Сколько граммов соли было в растворе первоначально?

1315. Вычислите устно:

1316.    При каких значениях а верно неравенство: а) а< — а; б) —а<а; в) —а>a?

1317.    Приведите подобные слагаемые:

1318.    Упростите выражение:

а) 2х—(x+ 1); б) n + 2(3n —1).

1319.    Расфасовочная машина может всю привезенную продукцию обработать за 20 ч. Определите: а) какую часть всей продукции она обработает за 1 ч; б) сколько процентов всей продукции она обработает за 1 ч; в) какую часть всей продукции она обработает за 8 ч; г) сколько процентов всей продукции она обработает за 9 ч.
1320.    За какое время все свекловичное поле уберет уборочная машина, если известно, что она за 1 ч убирает:
а) 5% всего поля; б) всего поля; в) 0,4 всего поля?
1321.    За какое время израсходует двигатель весь бензин из бака, если он: а) за 3 ч расходует 12% всего бензина; б) за 3 ч расходует всего бензина; в) за 6 ч расходует 0,24 всего 15 бензина?
1322.    Докажите, что при любом значении буквы значение выражения:

1)    5*(7y-2)-7*(5y + 2) равно -24;
2)    4*(8а + 3)—8*(4а — 3) равно 36.

1323.    Найдите значение выражения:

1)    (503,44:12,4 - 225,36:7,2)• (1,6905:0,49);
2)    (971,1:23,4 - 211,14:6,9)•(6,5704:0,86).

1324. Древнегреческая задача.
— Скажи мне, знаменитый Пифагор, сколько учеников посещают твою школу и слушают твои беседы.
— Вот сколько,— ответил Пифагор,— половина изучает математику, четверть — природу, седьмая часть проводит время в размышлении, и, кроме того, есть еще три женщины.
1325. Решите уравнение и выполните проверку:

1326.    Решите уравнение:

а)    -27x + 220=-5x; ж) -4*(-z + 7)=z + 17;
б)    7a=— 310 + 3а; 3) с-32=(с + 8)*(-7);
в)    -2x+16=5x—19; и) 12 — 2*(k + 3)= 26;
г)    25 — 3b = 9 — 5b; к) — 5(За + 1)-11 = —16;
д)    3 + 11y= 203 +y; Л) -3,2n + 4,8=-2*(1,2n+ 2,4);
е)    3*(4x — 8) = 3x — 6; м) -5*(0,8z-1,2)=-z + 7,2.

1327.    Одно число больше другого в 4,5 раза. Если от большего числа отнять 54, а к меньшему прибавить 72, то получатся равные результаты. Чему равны эти числа?

1328. Бутылка с кефиром в 2 раза тяжелее пустой бутылки (рис. 94). Галя выпила половину бутылки кефира. Сколько граммов кефира выпила Галя?
 

1329. У Миши и Коли было поровну денег. Когда Миша купил себе книгу, а Коля альбом, который в 1,4 раза дешевле книги, то у Миши осталось 20 к., а у Коли 40 к. Сколько стоит альбом, сколько стоит книга и сколько денег было у каждого мальчика?

1330. На одной полке было в 3 раз абольше книг, чем на другой. Когда с одной полки сняли 8 книг, а на другую положили 32, то книг на полках стало поровну. Сколько книг было на каждой полке первоначально?
 1331. В двух бочках 725 л бензина. Когда из первой бочки взяли , а из второй бензина, то в обеих бочках бензина стало поровну.Сколько литров бензина было в каждой бочке первоначально?

1332. Решите уравнение, используя основное свойство пропорции:

1333. Смешали индийский и грузинский чай. Индийский чай составил 30% всей смеси. Если в эту смесь добавить еще 120 г индийского чая, то он будет составлять 45% смеси. Сколько граммов индийского чая было в смеси первоначально?

1334. Поезд шел 3,5 ч со скоростью 64,4 км/ч. На сколько надо увеличить скорость поезда, чтобы пройти это расстояние за 2,8 ч?

1335. Одна поливочная машина может полить всю улицу за 15 мин, а другая — за 12 мин. Какую часть улицы польют обе машины за 1 мин? за 3 мин?

Среди задач, которые с давних времен приходилось решать людям, много было похожих, однотипных: вычисление площадей участков, нахождение объемов фигур определенной формы, деление доходов, вычисление стоимости товара, измерение массы с помощью различных единиц и другие.

Для однотипных задач в разное время, в разных странах пытались отыскать общие способы, правила решения. В этих правилах раскрывалось, как найти неизвестную величину через данные числа для группы похожих задач. Так возниклаАлгебра — один из разделов математики, в котором вначале в основном рассматривалось решение различных уравнений.

Некоторые алгебраические понятия и общие приемы решения задач знали уже в Древнем Вавилоне и Египте более 4000 лет назад. Большой вклад в создание алгебры внес выдающийся древнегреческий математик Диофант (III в.), которого по праву называют «отцом алгебры». Диофант умел решать очень сложные уравнения, применял для неизвестных буквенные обозначения, ввел специальный символ для вычитания, использовал сокращения слов.

В начале нашей эры греческая наука и культура пришли в упадок. Но к тому времени больших успехов в развитии математики достигли индийские ученые. С V по XII в. ими было сделано много открытий, значительно обогатились начала алгебры. Культуру древних индийцев усвоили их соседи — арабы, узбеки, персы, таджики и другие народы. И в IX—XV в. мировым центром наук становится Средняя Азия, подарившая миру много ученых-математиков. Их труды в дальнейшем оказали большое влияние на развитие науки в Европе.
 

В 825 г. арабский ученый а л ь-Х о р е з м й написал книгу «Китаб аль-джебр валь-мукабала», что означает «Книга о восстановлении и противопоставлении». Это был первый в мире учебник алгебры. С этого времени алгебра становится самостоятельной наукой. Само слово «алгебра» произошло от слова «аль-джебр» — восполнение: так аль-Хорезми называл перенос отрицательных слагаемых из одной части уравнения в другую с переменой знака. В дальнейшем большой вклад в развитие алгебры внесли европейские ученые Франсуа В и ё т (1540—1603) и Ренё Декарт, которые ввели в алгебру буквы и разработали правила действий с буквенными выражениями.

Н.Я.Виленкин, А.С. Чесноков, С.И. Шварцбурд, В.И.Жохов, Математика для 6 класса, Учебник для средней школы

_{Календарно-тематическое планирование по математике, задачи и ответы школьнику онлайн, курсы учителю по математике скачать}

Содержание урока
 конспект урока
 опорный каркас  
 презентация урока
 акселеративные методы 
 интерактивные технологии 

Практика
 задачи и упражнения 
 самопроверка
 практикумы, тренинги, кейсы, квесты
 домашние задания
 дискуссионные вопросы
 риторические вопросы от учеников

Иллюстрации
 аудио-, видеоклипы и мультимедиа 
 фотографии, картинки 
 графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты

Дополнения
 рефераты
 статьи 
 фишки для любознательных 
 шпаргалки 
 учебники основные и дополнительные
 словарь терминов                          
 прочие 

Совершенствование учебников и уроков
 исправление ошибок в учебнике
 обновление фрагмента в учебнике 
 элементы новаторства на уроке 
 замена устаревших знаний новыми 

Только для учителей
 идеальные уроки 
 календарный план на год  
 методические рекомендации  
 программы
 обсуждения


Интегрированные уроки

Если у вас есть исправления или предложения к данному уроку, напишите нам.

Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.