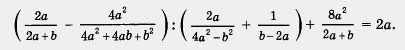Гипермаркет знаний>>Математика>>Математика 8 класс>>Математика:Преобразование рациональных выражений

Преобразование рациональных выражений

Этот параграф подводит итог всему тому, что мы, начиная с 7-го класса, говорили о математическом языке, о математической символике, о числах, переменных, степенях, многочленах и алгебраических дробях. Но сначала совершим небольшой экскурс в прошлое.

Вспомните, как в младших классах обстояло дело с изучением чисел и числовых выражений.

Сначала вы изучали натуральные числа A, 2, 3, 4, 5, ...) и операции над ними (но, конечно, этому предшествовало знакомство с цифрами). Затем появились целые числа (0, 1, -1, 2, -2, 3, -3, ...) — к ним относяся все натуральные числа, число 0 и целые отрицательные числа. Затем вы изучали рациональные числа — к ним относятся все целые числа и все дроби, как положительные, так и отрицательные. Таким образом, ко всякому натуральному числу, например к числу 2, можно «приклеить» три «ярлыка»: число 2 — натуральное, целое, рациональное. И это правильно, просто третий ярлык — рациональное число — достаточно широк, второй ярлык — целое число — поконкретнее, первый ярлык — натуральное число — самый конкретный.

Ко всякому целому числу, например к числу - 2, можно приклеить два ярлыка — целое число, рациональное число.

А, скажем, к дроби можно приклеить только один ярлык — рациональное число.

Аналогично обстоит дело с алгебраическими выражениями: первый этап их изучения — числа, переменные, степени («цифры»); второй этап их изучения — одночлены («натуральные числа»); третий этап их изучения — многочлены («целые числа»); четвертый этап их изучения — алгебраические дроби
(«рациональные числа»). При этом каждый следующий этап как бы вбирает в себя предыдущий: так, числа, переменные, степени — частные случаи одночленов; одночлены — частные •случаи многочленов; многочлены — частные случаи алгебраических дробей. Между прочим, в алгебре используют иногда и такие термины: многочлен — целое выражение, алгебраическая дробь — дробное выражение (это лишь усиливает аналогию).

Продолжим упомянутую аналогию. Вы знаете, что любое числовое выражение после выполнения всех входящих в его состав арифметических действий принимает конкретное числовое значение — рациональное число (разумеется, оно может оказаться и натуральным числом, и целым числом, и дробью — это неважно). Точно так же любое алгебраическое выражение, составленное из чисел и переменных с помощью арифметических операций и возведения в натуральную степень, после выполнения преобразований принимает вид алгебраической дроби и опять-таки, в частности, может получиться не дробь, а многочлен или даже одночлен). Для таких выражений в алгебре используют термин рациональное выражение.

Пример. Доказать тождество

Решение.
Доказать тождество — это значит установить, что при всех допустимых значениях переменных его левая и правая части представляют собой тождественно равные выражения. В алгебре тождества доказывают различными способами:

1) выполняют преобразования левой части и получают в итоге правую часть;

2) выполняют преобразования правой части и получают в итоге левую часть;

3) по отдельности преобразуют правую и левую части и получают и в первом и во втором случае одно и то же выражение;

4) составляют разность левой и правой частей и в результате ее преобразований получают нуль.

Какой способ выбрать — зависит от конкретного вида тождества, которое вам предлагается доказать. В данном примере целесообразно выбрать первый способ.

Для преобразования рациональных выражений принят тот же порядок действий, что и для преобразования числовых выражений. Это значит, что сначала выполняют действия в скобках, затем действия второй ступени (умножение, деление, возведение в степень), затем действия первой ступени (сложение, вычитание).

Выполним преобразования по действиям, опираясь на те правила, алгоритмы, что были выработаны в предыдущих параграфах.

Как видите, нам удалось преобразовать левую часть проверяемого тождества к виду правой части. Это значит, что тождество доказано. Однако напомним, что тождество справедливо лишь для допустимых значений переменных. Таковыми в данном примере являются любые значения а и b, кроме тех, которые обращают знаменатели дробей в нуль. Значит, допустимыми являются любые пары чисел (а; b), кроме тех, при которых выполняется хотя бы одно из равенств:

2а - b = 0, 2а + b = 0, b = 0.

Мордкович А. Г., Алгебра. 8 кл.: Учеб. для общеобразоват. учреждений.— 3-е изд., доработ. — М.: Мнемозина, 2001. — 223 с: ил.

_{Полный перечень тем по классам, календарный план согласно школьной программе по математике онлайн, видеоматериал по математике для 8 класса скачать}

Содержание урока
 конспект урока                       
 опорный каркас  
 презентация урока
 акселеративные методы 
 интерактивные технологии 

Практика
 задачи и упражнения 
 самопроверка
 практикумы, тренинги, кейсы, квесты
 домашние задания
 дискуссионные вопросы
 риторические вопросы от учеников

Иллюстрации
 аудио-, видеоклипы и мультимедиа 
 фотографии, картинки 
 графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты

Дополнения
 рефераты
 статьи 
 фишки для любознательных 
 шпаргалки 
 учебники основные и дополнительные
 словарь терминов                          
 прочие 

Совершенствование учебников и уроков
 исправление ошибок в учебнике
 обновление фрагмента в учебнике 
 элементы новаторства на уроке 
 замена устаревших знаний новыми 

Только для учителей
 идеальные уроки 
 календарный план на год  
 методические рекомендации  
 программы
 обсуждения


Интегрированные уроки

Если у вас есть исправления или предложения к данному уроку, напишите нам.

Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.