Інтегрований урок з математики та історії « Епоха розуму»
             Запропонований інтегрований урок “ Епоха розуму ” розрахований на дві академічні години, проводився у 9 і 10 класах. Об’єднання учнів у команди «Математики» і «Історики» відбувається  заздалегідь з урахуванням уподобань учнів.
                                                     “Недостатньо лише мати добрий розум, головне-–                                                      раціонально його використовувати”
                                                                                                                  Рене Декарт
         Мета:   розширити знання дітей про визначний вклад видатних постатей  науки у розвиток ХVІІ століття; сформувати уявлення про ідеї та методи математики, її роль у  пізнанні навколишнього світу;
сприяти розвитку розумової активності і пізнавальної  самостійності; виховувати інтерес до математики та історії
Обладнання:  проектор, персональний комп’ютер, роздатковий матеріал.
Хід уроку
 Вчитель історії: «Епоха розуму» (розповідь за слайдом)
 


                Вчитель математики:  Дійсно ХVІІ  ст. – є століттям «Епохи розуму». Адже воно нерозривно пов’язане з іменами великих вчених – Р.Декарта, І.Ньютона і Г.Лейбніца. Завдяки їхній праці випала можливість математично вивчати рух, процеси зміни величин і геометричних фігур. У математику входять поняття координат, змінних величин, функцій, диференціальне і інтегральне числення. З багатьма цими поняттями ви вже мали справу під час вивчення алгебри і тригонометрії. Але при цьому ви залишаєтесь лише біля порогу тієї математики, яка протягом останніх 300 років показала як незмінний інструмент виняткової сили і тонкості, що дав можливість поколінням астрологів, фізиків, механіків, представникам інших галузей науки вирішувати найважчі проблеми природознавства і техніки.
                   Вчитель історії: життєвий шлях та філософські погляди Р. Декарта(за слайдом)

 





                               Вчитель математики: 
               Так, Рене Декарт прожив відносно не довге життя (1596-1650), але його філософські погляди і роботи у сфері математики залишили великий слід.
               До  початку ХVІІ  ст. алгебра була вже досить розвинутою наукою, працями багатьох поколінь були підготовлені умови для нового великого відкриття у науці, що послужили поштовхом для її подальшого розвитку. Таким відкриттям стало введення у математику поняття змінної величини, функціональної залежності і прямокутної системи
координат.
                Декарт був великим і різнобічним вченим. Він займався філософією, фізіологією, фізикою, математикою. Так у математиці ним було зроблено різних ново відкриттів і нововведень, але найбільшою його заслугою є введення у математику поняття змінної величини, що він виклав у книзі «Геометрія», виданій у 1637 році (70 сторінок). Це відкриття назвали «поворотним пунктом у математиці».
 



                  Декарт ввів систему прямокутних координат, якою користуємося ми, в широке застосування і поклав початок розвиткові важливої математичної науки – аналітичної геометрії.
                 Основна думка Декарта полягала у тому, щоб примусити алгебру працювати на геометрію і навпаки. Алгебра має справу з числами та рівняннями, лініями, поверхнями. Як він поєднав ці дві науки? У системі координат встановлює відповідність між точкою і впорядкованою парою чисел – її координатами, потім – між кривою та її рівняннями.

       
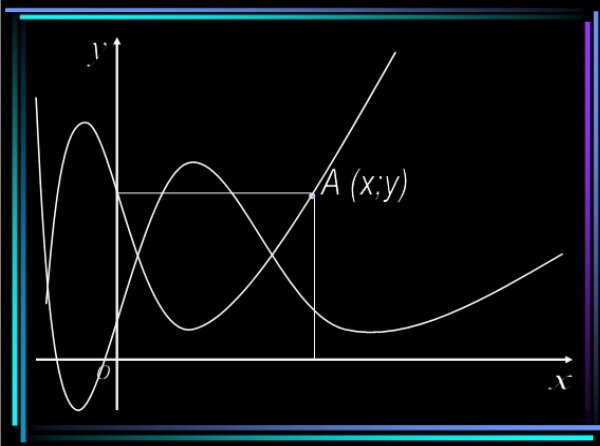
     Що ж це дало математиці? З’явилась можливість за рівнянням з двома змінними будувати  графік та описувати величини графічно. Коли ми бачимо температурну криву чи кардіограму, як штурман прокладає на карті маршрут корабля – це застосування нової геометрії. Навпаки, є можливість записувати рівняння ліній  та легко відповідати на запитання, чи вони перетинаються (якщо це навіть траєкторії космічних тіл), оскільки досить розв’язати  відповідну систему рівнянь. Так можна передбачити сонячні та місячні затемнення, «парад планет», можливість зіткнення комети із Землею. Метод координат подарував людству планету «на кінчику пера». Незалежно один від одного французький астроном Левер’є та англійський вчений Адамс під час дослідження відхилення від розрахункової орбіти у русі планети Уран, висунули припущення про існування невідомої досі планети Сонячної системи і розрахували її координати. Напрямлені телескопи у задані точки відправили в планету Сонячної системи – Нептун. А у 1915 році було математично доведено існування дев’ятої планети – Плутон, яку побачили у телескоп лише у 1930 році.
 

   Велика заслуга Р.Декарта у формуванні алгебри як науки. Для того щоб нерухомі точки А, В, С евклідових «Начал» вперше за 2 тисячі років зрушити з місця, Декарту потрібно було «тільки» 2 латинські букви х і у, якими він позначив змінні. Постійні величини позначав літерами a, b, c, степені  запропонував записувати так, як пишемо їх ми:  a  і т.д, алгебраїчні рівняння – в тому вигляді, в якому пишемо їх ми (нуль праворуч).
                 Згадаймо, як важко  проникали від’ємні числа, були вони і числами від сатани, і абсурдними, і хибними. Рене Декарт вводить знаки + і -  для позначення додатних і від’ємних чисел. Сучасне позначення кореня вперше з’явилося у працях Рене Декарта, він також дав правило знаходження числа додатних і від’ємних  коренів рівняння, заслуговують увагу результати в області розрахунків нескінченно малих величин, з його іменем пов’язані  такі поняття як добуток, парабола, лист, овал, циклоїда, дотична, логарифмічна спіраль і багато іншого. Тобто впродовж 150 років алгебра та аналітична геометрія розвивались у напрямку, що вказав Рене Декарт.
                          Декарт чимало зробив і для фізики. Саме він в оптиці встановив закон заломлення світла, створив теорію райдуги та з’ясував причину її виникнення. У механіці Рене указав на відносність руху та спокою, а також сформулював загальний закон дії і протидії та закон збереження певної кількості руху під час удару двох пружних тіл.
                 Конкурс «Видатна постать науки».
          Пропонується три сюжети, пов’язані з життям видатної особи, які потрібно відгадати. Після кожного сюжету учасники команд записують прізвище особи, про яку на їхню думку йдеться мова. (За правильну відповідь у кожному сюжеті видаються жетони червоного кольору, за неправильну відповідь – зеленого. У кінці уроку за кількістю отриманих жетонів вчителі історії і математики оцінюють роботу учасників команд.)

 

Конкурс «Художник-декоратор» 
            За координатами точок, потрібно намалювати високохудожній твір.
        (0;0), (-1;1), (-3;1), (-2;3), (-3;3), (-4;6), (0;8), (2;5), (2;11), (6;10), (3;9), (4;5), (3;0, (2;0),  (1;-7), (3;-8), (0;-8), (0;0).
Вчитель історії: життєвий шлях і філософські погляди В. Лейбніца(за слайдом)

 

                  Вчитель математики:
                 Про нього говорять, що до наших днів ніхто не поєднував такий яскравий математичний талант з такими широкими гуманітарними нахилами. Його поєднують з Арістотилем  або з  Леонардом да Вінчі. Лейбніц був вундеркіндом: у 8 років він самостійно вивчив латинь, а через два роки – древньогрецьку мову, у 15років стає студентом Лейпцігського університету, а у 20- магістром філософії, доктором права і дипломатом на службі у Курфюрста Майнцського. Наукова і громадсько-політична діяльність Лейбніца дуже різноманітна. Будучи передовою освіченою людиною, він тісно поєднував свої наукові дослідження з практикою, з потребами удосконалення техніки і природничих наук.
                 Але найбільшої слави здобув собі Лейбніц тим, що водночас з Ньютоном розробив основи диференціального та інтегрального числення, спираючись на розроблену Декартом аналітичну геометрію.
                 У проміжку між 1677 і 1684 роками у  своїх математичних працях вчений виклав відповідні правила без доведень, відразу показуючи їх практичне застосування, тобто правила диференціювання суми, добутку, частки, довільного сталого степеня, правила знаходження і встановлення екстремальних точок кривих, точок перегину, (за допомогою другого диференціалу), знайшов взаємно обернений зв'язок  між диференціюванням і інтегруванням, встановив формули для знаходження диференціалів вищого порядку, правила диференціювання важливих трансцендентних функцій, раціональних дробів, розкладав функції у нескінченні степеневі ряди, дав ознаки збіжності знакозмінних рядів та способи розв’язування диференціальних рівнянь. З цим ми зустрічаємось під час вивчення  математики  в 11 класі або у вищій школі.

 

                   Лейбніц ввів терміни і знаки, якими ми користуємося сьогодні, це: знаки множення, ділення, дужки, які необхідні у формулах і різних математичних перетвореннях,  знаки для диференціалу і інтегралу, терміни «диференціал, диференціальні числення», «функція», «змінна», «стала», «ордината», «абсциса»і т.д.
                    Великий вчений зробив ряд важливих відкриттів і у інших галузях математики: в комбінаториці, в алгебрі (теорія визначників), в геометрії (теорія дотичних кривих).
                    Диференціальне та інтегральне числення  виявилось корисним і для розв’язання  задач з фізики, механіки, геодезії. Будучи передовою освіченою людиною, він тісно поєднував свої наукові дослідження з практикою, з потребами удосконалення техніки і природничих наук.
                    Лейбніц брав безпосередню участь у створенні «прабабусі» сучасного калькулятора. Так, коли він познайомився з голландським математиком і астрологом Гюйгенсом і побачив, як багато обчислень доводиться виконувати останньому, то вирішив віднайти механічний пристрій, який полегшив би лічбу. У 1663 році він виготовив механічний калькулятор. Вчений продемонстрував свою машину у Французькій академії наук і Лондонському королівському товаристві. Одна така машина Лейбніца потрапила навіть до Петра I, а той подарував її китайському імператорові, маючи на меті вразити його європейськими технічними досягненнями. Заклав також основи двійкової системи числення, яка пізніше знайшла застосування в автоматичних обчислювальних приладах, зокрема у комп’ютері.
               Учений висунув ідею застосування циліндра і поршня в машинах, яка пізніше була використана у конструюванні парових двигунів.    
                Творчість Лейбніца мала велике значення для розвитку світової науки. У 1697 році  вперше він зустрічається з Петром Великим, який прибув у Голландію для вивчення морської справи. Тоді вчений запропонував проект реформи освіти в Росії і проект створення Петербурзької Академії наук. Восени  наступного року Петро Перший зустрічається з Лейбніцом, який передає йому план створення Академії наук, за що був нагороджений званням таємного радника юстиції російської служби.
                      Берлінська академія наук була теж заснована за пропозицією талановитої людини Лейбніца і він стає першим її президентом.
                      Поет Брюсов писав: «О Лейбніц, о мудрець, засновник віщих книг! Ти вище світу був, як древнії пророки». Захоплювався він і музикою, бачив нерозривний зв'язок її з математикою. Ось таке означення він дає музиці: «Музика – є арифметична вправа для душі».
                      А от обставини смерті вченого досить дивні. 14 листопада 1716 року вчений почував себе гірше, від звичайного. Давній знайомий, що прийшов його відвідати, напоїв його настоєм якогось зілля. Випивши її, Лейбніцу погіршало, і поки прийшов лікар, вчений помер. За труною людини, яка у свій час була гордістю Європейської науки, йшла тільки одна особа – секретар вченого.

          Конкурс «Видатна постать науки»
 


        Конкурс «Відгадай Анаграму»
Розв’язати анаграму та виключити зайве слово у такому переліку
Тадкер, тьонюн, гносканте, бейлцін.
Відповідь до завдання: Декарт, Ньютон, котангенс, Лейбніц.
Вчитель історії: життєвий шлях і філософські погляди І. Ньютона (за слайдом)
 

                  Вчитель математики:
               Якщо змінна Декарта відкрила перед математикою перспективу описання процесів, то похідна Ньютона послужила їй досконалим інструментом для цього описання. За словами самого Ньютона, найбільш плідними у його науковій роботі були 1665 – 1666 роки.
                В історії науки, мабуть, не знайти досягнень, які б могли б зрівнятися з працями Ньютона у ці два золоті роки. Він перший (одночасно з Лейбніцом) створив основи диференціального та інтегрального числення. Введенню поняття похідної, диференціалів, інтеграла, передували роботи багатьох математиків. Зокрема, Архімед ще в III ст. до н.е. розробив методи для знаходження площ і об’ємів геометричних фігур. Але ті задачі розв’язувалися досить важкими, штучними методами, а в багатьох випадках і зовсім не вдавалось знайти відповідь.
 
              Основна заслуга Ньютона і Лейбніца в тому, що вони пов’язали диференціальне числення з інтегральним, створивши тим самим найважливішу науку – математичний аналіз. Спеціалісти вважають відкриття математичного аналізу – найбільшим відкриттям людства XVII ст. Ньютон здійснює відкриття в області нескінченних рядів, встановлює біном Ньютона, розвиває аналітичну теорію тригонометричних і обернено тригонометричних функцій, розвиває вчення про границі, дає теорію конічних перерізів, розглядає криві третього, другого порядків, та їх способи побудови і властивості. Ці праці велику роль відіграли в аналітичній геометрії.
               Всім, мабуть, відомий анекдот про те, як Ньютон у саду спостерігав за яблуками, що падали з дерев. І це начебто наштовхнуло його на відкриття  одного з основних законів, які керують природою, - закону всесвітнього тяжіння. Це звичайно, тільки анекдот, тому що створення теорії гравітації не було випадковим, а було плодом геніального розуму великого фізика і математика. Найвидатніший твір Ньтона мав назву «Математичні начала натуральної філософії» (1687 р.) В ньому Ньютон дав визначення трьох основних принципів класичної механіки і визначив закон тяжіння, на підставі якого розробив теорію руху планети. І пояснив багато інших проблем астрономії (зокрема, причину морських припливів та відпливів, що викликаються притяганням місяця), фізики (вказав на те, що промінь білого світла після проходження через призму розщеплюється на промені різних кольорів).
                  Будучи великим вченим, Ньютон не вихвалявся своїми відкриттями, а завжди віддавав належну шану своїм попередникам і сучасникам. Він дуже пізно друкував свої праці. Закон всесвітнього тяжіння він опублікував через 20 років. Теж саме вийшло з основами диференціального числення, коли подібна праця вийшла у Лейбніца, а Ньютон написав її на 10 років раніше.
                   У повсякденному житті він дотримувався суворого режиму. Цим загартовував свій організм і до 80 років був міцним і здоровим. Він настільки був захоплений наукою, що просто забував поїсти, поспати. Очевидці твердять, що він дуже не любив, коли йому доводилось відриватись від своїх занять. І щоб його кішка могла заходити в кабінет, не відриваючи хазяїна від справи, він у дверях зробив отвір. А коли у кішки з’явилися кошенята, то він додатково проробив отвори для кожного кошеняти.
          Конкурс «Видатна постать науки»
 
Тестові завдання
Вчитель історії:
 
Вчитель математики:
 

Підсумок уроку
 

 


 
Домашнє завдання

Підготувати реферати на тему: «Цікаві історичні факти із життя вчених » (І.Ньютона, Г. Лейбніца, Р. Декарта), скласти анаграми, кросворди.