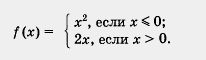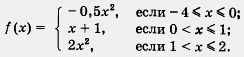Гипермаркет знаний>>Математика>>Математика 8 класс>>Математика:Функция у = kx2, ее свойства и график

ФУНКЦИЯ у = кх1, ЕЕ СВОЙСТВА И ГРАФИК

В 7-м классе мы изучали функции у = С, у = kx, у = kx + m, у = х² и пришли в итоге к выводу о том, что уравнение с двумя переменными вида у = f(x) (функция) есть математическая модель, удобная для того, чтобы, задав конкретное значение независимой переменной х (аргумента), вычислить соот-
ветствующее значение зависимой переменной у. Например, если дана функция у = х², т.е. f(x) = х², то при х = 1 получаем у = 1² = 1; короче это записывают так: f(1) = 1. При х = 2 получаем f(2)= 2² = 4, т. е. у = 4; при х = - 3 получаем f(- 3) = (- З)² = 9, т. е. у = 9, и т. д.

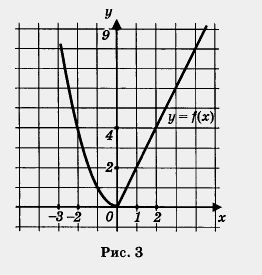
Уже в 7-м классе мы с вами начали понимать, что в равенстве у = f(х) правая часть, т.е. выражение f(x), не исчерпывается перечисленными выше четырьмя случаями (С, kx, kx + m, х²).
Так например, нам уже встречались кусочные функции, т. е. функции, заданные разными формулами на разных промежутках. Вот одна из таких функций:

у = f(x), где

Помните, как строить графики таких функций? Сначала надо построить параболу у = х² и взять ее часть при х < 0 (левая ветвь параболы, рис. 1), затем надо построить прямую у = 2х и взять ее часть при х > 0 (рис. 2). И, наконец, надо обе выделенные части объединить на одном рисунке, т. е. построить на одной координатной плоскости (см. рис. 3).

Теперь наша задача состоит в следующем: пополнить запас изученных функций. В реальной жизни встречаются процессы, описываемые различными математическими моделями вида у = f(x), не только теми, что мы перечислили выше. В этом параграфе мы рассмотрим функцию у = kx², где коэффициент k — любое отличное от нуля число.

На самом деле функция у = kx² в одном случае вам немного знакома. Смотрите: если k = 1, то получаем у = х²; эту функцию вы изучили в 7-м классе и, наверное, помните, что ее графиком является парабола (рис. 1). Обсудим, что происходит при других значениях коэффициента k.
Рассмотрим две функции: у = 2х² и у = 0,5x². Составим таблицу значений для первой функции у = 2х²:

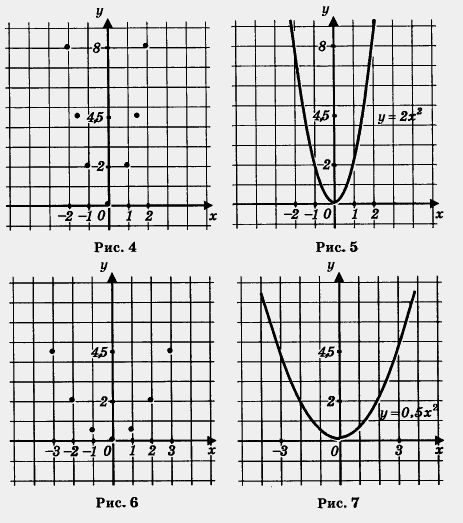
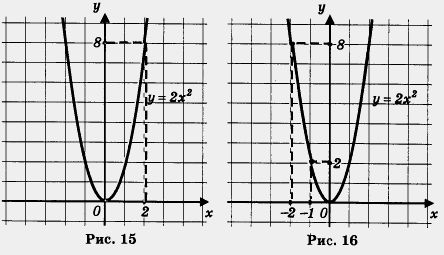
Построим точки (0; 0), (1; 2), (-1; 2), (2; 8), (-2; 8), (1,5; 4,5), (-1,5; 4,5) на координатной плоскости (рис. 4); они намечают некоторую линию, проведем ее

(рис. 5).
Составим таблицу значений для второй функции у = 0,5x²:

Построим точки (0; 0), (1; 0,5), (-1; 0,5), (2; 2), (-2; 2), C; 4,5), (-3; 4,5) на координатной плоскости (рис. 6); они намечают некоторую линию, проведем ее (рис. 7) 

.

Точки, изображенные на рис. 4 и 6, называют иногда контрольными точками для графика соответствующей функции.

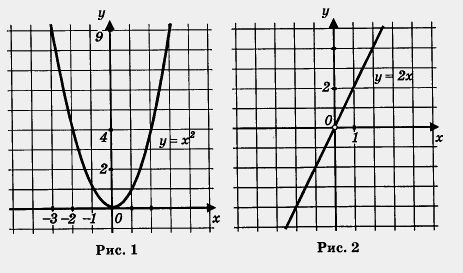
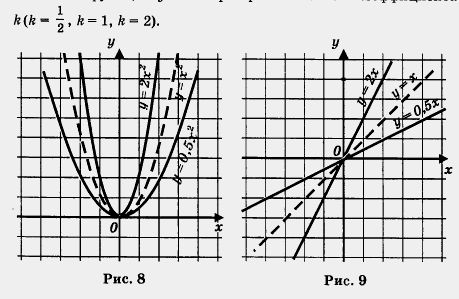
Сравните рисунки 1, 5 и 7. Не правда ли, проведенные линии похожи? Каждую из них называют параболой; при этом точку (0; 0) называют вершиной параболы, а ось у — осью симметрии параболы. От величины коэффициента k зависит «скорость устремления» ветвей параболы вверх или, как еще говорят,
«степень крутизны» параболы. Это хорошо видно на рис. 8, где все три построенные выше параболы расположены на одной координатной плоскости.

Точно так же обстоит дело с любой другой функцией вида у = kx², где k > 0. Графиком ее является парабола с вершиной в начале координат, ветви параболы направлены вверх, причем тем круче, чем больше коэффициент k. Ось у является осью симметрии параболы. Кстати, ради краткости речи математики часто вместо длинной фразы «парабола, служащая графиком функции у = kx²», говорят «парабола у = кх²», а вместо термина «ось симметрии параболы» используют термин «ось параболы».

Вы замечаете, что имеется аналогия с функцией у = kx? Если k > 0, то графиком функции у = kx является прямая, проходящая через начало координат (помните, мы говорили коротко:прямая у = kx), причем и здесь от величины коэффициента k зависит «степень крутизны» прямой. Это хорошо видно на
рис. 9, где в одной системе координат изображены графики линейных функций у = kx при трех значениях коэффициента

Вернемся к функции у = kx². Выясним, как обстоит дело в случае отрицательного коэффициента ft. Построим, например, график функции

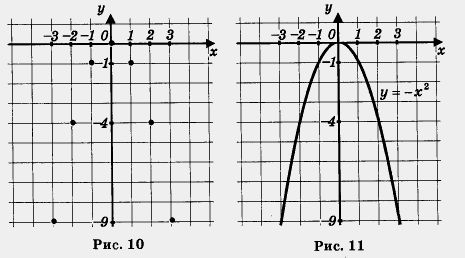
у = - х² (здесь k = - 1). Составим таблицу значении:

Отметим точки (0; 0), (1; -1), (-1; -1), (2; -4), (-2; -4), (3; -9), (- 3; - 9) на координатной плоскости (рис. 10); они намечают некоторую линию, проведем ее (рис. 11). Это — парабола с вершиной в точке (0; 0), ось у — ось симметрии, но в отличие от случая, когда k > 0, на этот раз ветви параболы направлены вниз. Аналогично обстоит дело и для других отрицательных значений коэффициента k.

Итак, графиком функции является парабола с вершиной в начале координат; ось у является осью параболы; ветви параболы направлены вверх приk>0 u вниз при k<0.

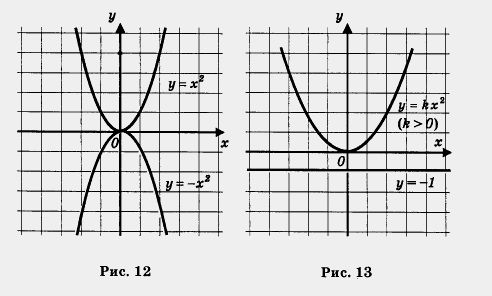
Отметим еще, что парабола у = kx² касается оси х в точке (0; 0), т. е. одна ветвь параболы плавно переходит в другую, как бы прижимаясь к оси х.
Если построить в одной системе координат графики функций у = х² и у = - х2, то нетрудно заметить, что эти параболы симметричны друг другу относительно оси х, что хорошо видно на рис. 12. Точно так же симметричны друг другу относительно оси х параболы у = 2х² и у = - 2х² (не поленитесь, постройте эти
две параболы в одной системе координат и убедитесь в справедливости сделанного утверждения).

Вообще, график функции у = - f(x) симметричен графику функции у = f(x) относительно оси абсцисс.

                                    Свойства функции у = kx² при k > 0

Описывая свойства этой функции, мы будем опираться на ее геометрическую модель — параболу (рис. 13).

1. Так как для любого значения х по формуле у = kx² можно вычислить соответствующее значение у, то функция определена в любой точке х (при любом значении аргумента х). Короче это записывают так: область определения функции есть (-оо, +оо), т. е. вся координатная прямая.

2. у = 0 при х = 0; у > О при . Это видно и по графику функции (он весь расположен выше оси х), но можно обосновать и без помощи графика: если

, то kx² > О как произведение двух положительных чисел k и х².

3. у = kx² — непрерывная функция. Напомним, что этот термин мы рассматриваем пока как синоним предложения «график функции есть сплошная линия, которую можно начертить, не отрывая карандаша от бумаги». В старших классах будет дано более точное математическое истолкование понятия непрерывности функции, не опирающееся на геометрическую иллюстрацию.

4.y/_наим = 0 (достигается при х = 0); у_наи6 не существует.

Напомним, что {/наим — это наименьшее значение функции, а Унаиб. — наибольшее значение функции на заданном промежутке; если промежуток не указан, то унаим- и у_наиб, — соответственно наименьшее и наибольшее значения функции в области определения.

5. Функция у = kx² возрастает при х > О и убывает при х < 0.

Напомним, что в курсе алгебры 7-го класса мы договорились называть функцию, график которой на рассматриваемом промежутке идет слева направо как бы «в горку», возрастающей, а функцию, график которой на рассматриваемом промежутке идет слева направо как бы «под горку», — убывающей. Более точно можно сказать так: функцию у = f (x) называют возрастающей на промежутке X, если на этом промежутке большему значению аргумента соответствует
большее значение функции; функцию у = f (x) называют убывающей на промежутке X, если на этом промежутке большему значению аргумента соответствует меньшее значение функции.

В учебнике «Алгебра—7» процесс перечисления свойств функции мы называли чтением графика. Процесс чтения графика будет у нас постепенно становиться все насыщеннее и интереснее — по мере изучения новых свойств функций. Те пять свойств, которые перечислены выше, мы обсуждали в 7-м классе для изученных там функций. Добавим одно новое свойство.

Функцию у = f(x) называют ограниченной снизу, если все значения функции больше некоторого числа. Геометрически это означает, что график функции расположен выше некоторой прямой, параллельной оси х.

А теперь посмотрите: график функции у = kx² расположен выше прямой у = - 1 (или у = - 2, это неважно) — она проведена на рис. 13. Значит, у — kx2 (k > 0) — ограниченная снизу функция.

Наряду с функциями, ограниченными снизу, рассматривают и функции, ограниченные сверху. Функцию у — f(x) называют ограниченной сверху, если все значения функции меньше некоторого числа. Геометрически это означает, что график функции расположен ниже некоторой прямой, параллельной оси х.
Имеется ли такая прямая для параболы у = kx², где k > 0? Нет. Это значит, что функция не является ограниченной сверху.

Итак, мы получили еще одно свойство, добавим его к тем пяти, что указаны выше.

6. Функция у = kx² (k > 0) ограничена снизу и не ограничена сверху.

                                                 Свойства функции у = kx² при k < 0

При описании свойств этой функции мы опираемся на ее геометрическую модель — параболу (рис. 14).

1.Область определения функции — (—оо, +оо).

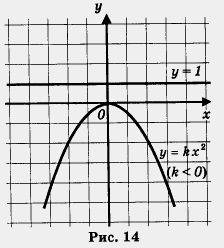
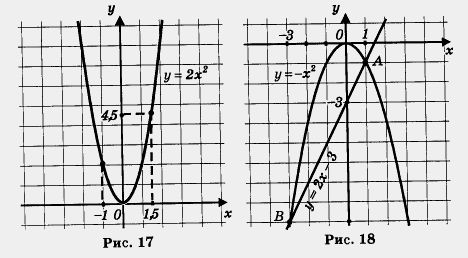
2. у = 0 при х = 0; у < 0 при .

З.у = kx² — непрерывная функция.
4. у_наи6 = 0 (достигается при х = 0), унаим не существует.

5. Функция возрастает при х < 0, убывает при х > 0.

6.Функция ограничена сверху и не ограничена снизу.

Дадим пояснения последнему свойству: имеется прямая, параллельная оси х (например, у = 1, она проведена на рис. 14), такая, что вся парабола лежит ниже этой прямой; это значит, что функция ограничена сверху. С другой стороны, нельзя провести такую прямую, параллельную оси х, чтобы вся парабола была расположена выше этой прямой; это значит, что функция не ограничена снизу.

Использованный выше порядок ходов при перечислении свойств функции не является законом, пока он сложился хронологически именно таким.

Более-менее определенный порядок ходов мы выработаем постепенно и унифицируем в курсе алгебры 9-го класса.

Пример 1. Найти наименьшее и наибольшее значения функции у = 2х² на отрезке: а) [0, 2]; б) [- 2, - 1]; в) [- 1, 1,5].

Решение.
а) Построим график функции у = 2х² и выделим его часть на отрезке [0, 2] (рис. 15). Замечаем, что 1/наим. = 0 (достигается при х = 0), а у_наиб = 8 (достигается при х = 2).

б) Построим график функции у = 2х² и выделим его часть на отрезке [- 2, - 1] (рис. 16). Замечаем, что 2/наим = 2 (достигается при х = - 1), а y_наиб = 8 (достигается при х = - 2).

в) Построим график функции у = 2х² и выделим его часть на отрезке [- 1, 1,5] (рис. 17). Замечаем, что унанм = 0 (достигается при х = 0), а y_наиб достигается в точке х = 1,5; подсчитаем это значение:(1,5) = 2-1,5² = 2- 2,25 = 4,5. Итак, y_наиб =4,5. 

Пример 2. Решить уравнение - х² = 2х - 3.

Решение. В учебнике «Алгебра—7» мы выработали алгоритм графического решения уравнений, напомним его.

Чтобы графически решить уравнение f(x) = g (x), нужно:

1) рассмотреть две функции у = -x² и у = 2x -3;
2) построить график функции i/ = / (х) ;
3) построить график функции у = g (x);
4) найти точки пересечения построенных графиков; абсцис-
сы этих точек — корни уравнения f(x) = g (x).
Применим этот алгоритм к заданному уравнению.
1) Рассмотрим две функции: у = - х2 и у = 2х - 3.
2) Построим параболу — график функции у = - х² (рис. 18).

3) Построим график функции у = 2х - 3. Это — прямая, для ее построения достаточно найти любые две точки графика. Если х = 0, то у = - 3; если х = 1,

то у = -1. Итак, нашли две точки (0; -3) и (1; -1). Прямая, проходящая через эти две точки (график функции у = 2х - 3), изображена на том же

чертеже (см. рис. 18).

4) По чертежу находим, что прямая и парабола пересекаются в двух точках А(1; -1) и Б(-3; -9). Значит, данное уравнение имеет два корня: 1 и - 3 — это абсциссы точек А и В.

Ответ: 1,-3.

Замечание. Разумеется, нельзя слепо доверять графическим иллюстрациям. Может быть, нам только кажется, что точка А имеет координаты (1; — 1), а на
самом деле они другие, например (0,98; - 1,01)?

Поэтому всегда полезно проверить себя. Так, в рассмотренном примере надо убедиться, что точка А(1; —1) принадлежит параболе у = — х² (это легко — достаточно подставить в формулу у = — х² координаты точки А; получим - 1 = - 1² — верное числовое равенство) и прямой у = 2х - 3 (и это легко — достаточно подставить в формулу у = 2х - 3 координаты точки А; получим - 1 =2-3 — верное числовое равенство). То же самое надо сделать и для
точки 8. Эта проверка показывает, что в рассмотренном уравнении графические наблюдения привели к верному результату.

Пример 3. Решить систему уравнений

Решение. Преобразуем первое уравнение системы к виду у = - х². Графиком этой функции является парабола, изображенная на рис. 18.
Преобразуем второе уравнение системы к виду у = 2х - 3. Графиком этой функции является прямая, изображенная на рис. 18.

Парабола и прямая пересекаются в точках А(1; -1) и В (- 3; - 9). Координаты этих точек и служат решениями заданной системы уравнений.

Ответ: (1; -1), (-3; -9).

Пример 4. Дана функция у — f (x), где

Требуется:

а) вычислить f(-4), f(-2), f(0), f(1,5), f(2), f(3);

б) построить график функции;

в) с помощью графика перечислить свойства функции.

Решение,

а) Значение х = - 4 удовлетворяет условию —, следовательно, f(-4) надо вычислять по первой строке задания функции.Имеем f(x) = - 0,5x2, значит,
f(-4) = -0,5.(-4)² = -8.
Аналогично находим:

f(-2) = -0,5.(-2)²=-2;
f(0) = -0,5. 0² = 0.

Значение удовлетворяет условию , поэтому надо вычислять по второй строке задания функции. Имеем f(х) = х + 1, значит,

  Значение х = 1,5 удовлетворяет условию 1 < х < 2, т. е. f(1,5) надо вычислять по третьей строке задания функции. Имеем f (х) = 2х² , значит,
f(1,5) = 2-1,5² = 4,5.
Аналогично получим
 f(2)= 2.2²=8.
Значение х = 3 не удовлетворяет ни одному из трех условий задания функции, а потому f(3) в данном случае вычислить нельзя, точка х = 3 не принадлежит области определения функции. Задание, состоящее в том, чтобы вычислить f(3), — некорректно.

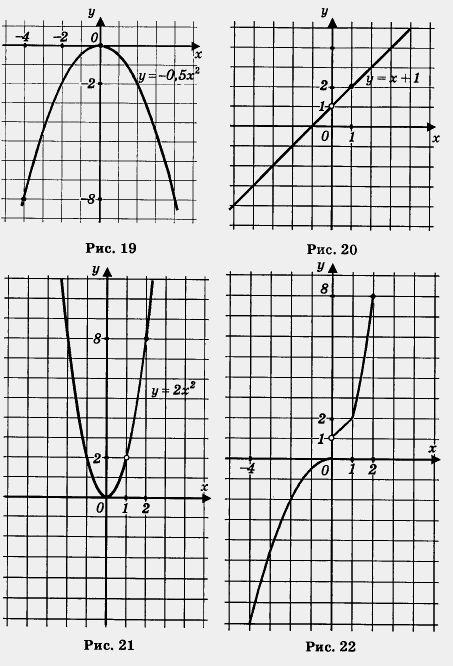
б) Построение графика осуществим «по кусочкам». Сначала построим параболу у = -0,5x² и выделим ее часть на отрезке [-4, 0] (рис. 19). Затем построим прямую у = х + 1 и. выделим ее часть на полуинтервале (0, 1] (рис. 20). Далее построим параболу у = 2х² и выделим ее часть на полуинтервале

(1, 2] (рис. 21).

Наконец, все три «кусочка» изобразим в одной системе координат; получим график функции у = f(x) (рис. 22).

в) Перечислим свойства функции или, как мы условились говорить, прочитаем график.

1. Область определения функции — отрезок [—4, 2].

2. у = 0 при х = 0; у > 0 при 0<х<2;у<0 при - 4 < х < 0.

3. Функция претерпевает разрыв при х = 0.

4. Функция возрастает на отрезке [-4, 2].

5. Функция ограничена и снизу и сверху.

6. y_наим = -8 (достигается при х = -4); y_наи6. = 8 (достигается при х = 2).

Пример 5. Дана функция у = f(x) , где f(x) = Зх². Найти:

f(1), f(- 2), f(а), f(2а), f(а + 1), f(-х), f(Зх),f(x - 1),
f(x + а), f(x) + 5, f(х) + b, f(x + а) + b, f(x²), f(2х³).

Решение. Так как f (х) = Зх², то последовательно получаем:

f(1) =3.1² = 3;    
f(a) = За²;
f(а+1) = 3(а + 1)²;
f(3х) = 3.(3х)² = 27х²;
f(x + а) = 3(х + а)²;

f( x²) +b = 3x² +b
f(x²) = 3. (x²)^{2</sup = 3x4}

^{f(- 2) = З.(-2)2 = 12
f( 2a) =З.(2a)2 =12a2}

^{f(x) =З.(-x)2 =3x2}

<sup>f(-x)+ 5 =3x2 +5
f{x + а) + b = 3 (x + a)2 + b;
f(2x3) = 3. (2x3)2</sup = 12x6



_{Планирование математике, материалы по математике 8 класса скачать, учебники онлайн}</sup>

Содержание урока
 конспект урока                       
 опорный каркас  
 презентация урока
 акселеративные методы 
 интерактивные технологии 

Практика
 задачи и упражнения 
 самопроверка
 практикумы, тренинги, кейсы, квесты
 домашние задания
 дискуссионные вопросы
 риторические вопросы от учеников
 
Иллюстрации
 аудио-, видеоклипы и мультимедиа 
 фотографии, картинки 
 графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты

Дополнения
 рефераты
 статьи 
 фишки для любознательных 
 шпаргалки 
 учебники основные и дополнительные
 словарь терминов                          
 прочие 

Совершенствование учебников и уроков
 исправление ошибок в учебнике
 обновление фрагмента в учебнике 
 элементы новаторства на уроке 
 замена устаревших знаний новыми 
 
Только для учителей
 идеальные уроки 
 календарный план на год  
 методические рекомендации  
 программы
 обсуждения


Интегрированные уроки

^{Если у вас есть исправления или предложения к данному уроку, напишите нам.}

^{Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.}