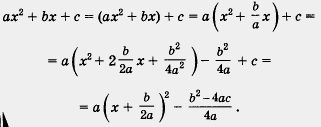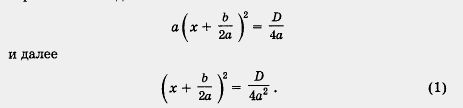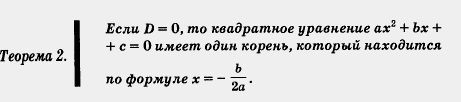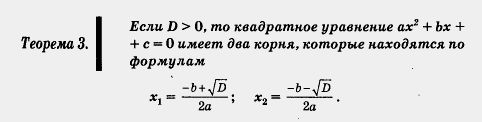|
Гипермаркет знаний>>Математика>>Математика 8 класс>>Математика:Формулы корней квадратных уравнений
ФОРМУЛЫ КОРНЕЙ КВАДРАТНЫХ УРАВНЕНИЙ
Пусть дано квадратное уравнение ах2 + bх + с = 0.
Применим к квадратному трехчлену ах2 + bх + с те же преобразования, которые мы выполняли в § 13, когда доказывали теорему о том, что графиком функции у = ах2 + bх + с является парабола.
Имеем
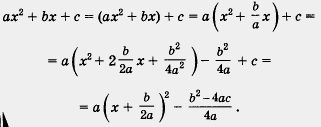
Обычно выражение b2 - 4ас обозначают буквой D и называют дискриминантом квадратного уравнения ах2 + bх + с = 0 (или дискриминантом квадратного трехчлена ах + bх + с).
Таким образом
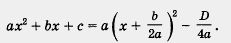
Значит, квадратное уравнение ах2 + их + с = О можно переписать в виде
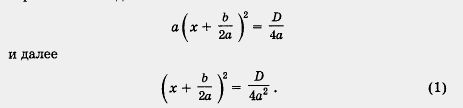
Любое квадратное уравнение можно преобразовать к виду (1), удобному, как мы сейчас убедимся, для того, чтобы определять число корней квадратного уравнения и находить эти корни.
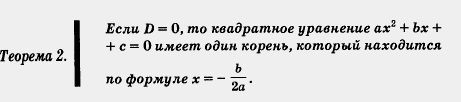
Доказательство. Если D < 0, то правая часть уравнения (1) — отрицательное число; в то же время левая часть уравнения (1) при любых значениях х принимает неотрицательные значения. Значит, нет ни одного значения х, которое удовлетворяло бы уравнению (1), а потому уравнение (1) не имеет корней.
Пример 1. Решить уравнение 2x2 + 4х + 7 = 0.
Решение. Здесь а = 2, b = 4, с = 7,
D = b2-4ac = 42. 4. 2. 7 = 16-56 = -40.
Так как D < 0, то по теореме 1 данное квадратное уравнение не имеет корней.
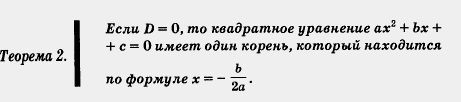
Доказательство. Если D = 0, то уравнение (1) принимает вид
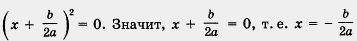 — единственный корень уравнения. — единственный корень уравнения.
Замечание 1. Помните ли вы, что х = - 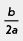 — абсцисса вершины параболы, которая служит графиком функции у = ах2 + их + с? Почему именно это — абсцисса вершины параболы, которая служит графиком функции у = ах2 + их + с? Почему именно это
значение оказалось единственным корнем квадратного уравнения ах2 + их + с — 0? «Ларчик» открывается просто: если D — 0, то, как мы установили ранее,
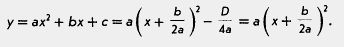
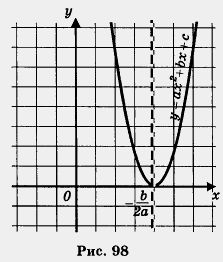
Графиком же функции 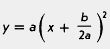 является парабола с вершиной в точке является парабола с вершиной в точке 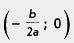 (см., например, рис. 98). Значит, абсцисса вершины параболы и единственный корень квадратного уравнения при D = 0 — одно и то же число. (см., например, рис. 98). Значит, абсцисса вершины параболы и единственный корень квадратного уравнения при D = 0 — одно и то же число.
Пример 2. Решить уравнение 4x2 - 20x + 25 = 0.
Решение. Здесь а = 4, b = -20, с = 25, D = b2 - 4ас = (-20)2 - 4 • 4 • 25 = 400 - 400 = 0.
Так как D = 0, то по теореме 2 данное квадратное уравнение имеет один корень. Этот корень находится по формуле
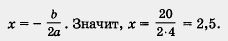
Ответ: 2,5.
Замечание 2. Обратите внимание, что 4х2 - 20х +25 — полный квадрат: 4х2 - 20х + 25 = (2х - 5)2.
Если бы мы это заметили сразу, то решили бы уравнение так: (2х - 5)2 = 0, значит, 2х - 5 = 0, откуда получаем х = 2,5. Вообще, если D = 0, то
ах2 + bх + с = 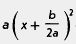 — это мы отметили ранее в замечании 1. — это мы отметили ранее в замечании 1.
Если D > 0, то квадратное уравнение ах2 + bх + с = 0 имеет два корня, которые находятся по формулам
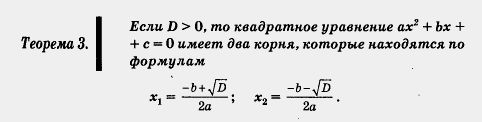
Доказательство. Перепишем квадратное уравнение ах2 + Ьх + с = 0 в виде (1)
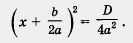
Положим 
По условию, D > 0, значит, правая часть уравнения положительное число. Тогда из уравнения (2) получаем, что

Итак, заданное квадратное уравнение имеет два корня:
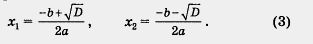
Замечание 3. В математике довольно редко бывает так, чтобы введенный термин не имел, образно выражаясь, житейской подоплеки. Возьмем новое
понятие — дискриминант. Вспомните слово «дискриминация». Что оно означает? Оно означает унижение одних и возвышение других, т.е. различное отноше-
ние к различным пюдям. Оба слова (и дискриминант, и дискриминация) происходят от латинского discriminans — «различающий». Дискриминант различает квадратные уравнения по числу корней.
Пример 3. Решить уравнение Зх2 + 8х - 11 = 0.
Решение. Здесь а = 3, Ъ = 8, с = - 11,
D = Ь2 - 4ас = 82 - 4 • 3 • (-11) = 64 + 132 = 196.
Так как D > 0, то по теореме 3 данное квадратное уравнение
имеет два корня. Эти корни находятся по формулам C)
-b + JP -8 + ^196 -8 + 14
1
2а
-8->/i96 -8-14
П
2а
2
Ответ: 1; -3 , •
Фактически мы с вами выработали следующее правило:
Правило решения уравнения
ах2 + Ъх + с = 0
1. Вычислить дискриминант D по формуле
D = b2- 4ac.
2. Если D < О, то квадратное уравнение не
имеет корней.
3. Если D = О, то квадратное уравнение име-
ет один корень:
__Ъ_
4. Если D > О, то квадратное уравнение
имеет два корня:
х, =
2а
-ь-л/д
2а
Это правило универсально, оно применимо как к полным, так и
к неполным квадратным уравнениям. Однако неполные
квадратные уравнения обычно по этому правилу не решают, их
удобнее решать так, как мы это делали в предыдущем параграфе.
Пример 4. Решить уравнения:
а) х2 + Зх - 5 = 0; б) - 9*2 + 6х - 1 = 0; в) 2х2-х + 3,5 = 0.
Р е ш е н и е. а) Здесь а = 1, Ъ = 3, с = - 5,
D = Ъ2 - 4ас = З2 - 4 • 1 • (- 5) = 9 + 20 = 29.
Так как D > 0, то данное квадратное уравнение имеет два
корня. Эти корни находим по формулам C)
-b+J5 -3+V29
1 2а 2 '
хо =
-3-V29
2а 2
б) Как показывает опыт, удобнее иметь дело с
квадратными уравнениями, у которых старший
коэффициент положителен. Поэтому сначала
умножим обе части уравнения на -1, получим
9*2 - 6* + 1 = 0.
Здесь а = 9, Ь = -6, с = 1, D = Ь2 - Аас = 36 - 36 = 0.
Так как D = 0, то данное квадратное уравнение имеет один
b
корень. Этот корень находится по формуле х = - —. Значит,
6 1.
Х= 2^9 ~3"
Это уравнение можно было решить по-другому: так как
Эх2 - 6* + 1 = (Зх - IJ, то получаем уравнение (Зх - IJ = 0,
откуда находим Зх - 1 = 0, т. е. х = - .
в) Здесь а = 2, b = - 1, с = 3,5, D = Ъ2 - 4ас = 1 - 4 • 2 • 3,5 =
= 1 - 28 = - 27. Так как D < 0, то данное квадратное уравнение не
имеет корней. <Ц
Математики — люди практичные, экономные. Зачем, гово-
рят они, пользоваться таким длинным правилом решения квад-
ратного уравнения, лучше сразу написать общую формулу:
х
1.2
2а
D)
Если окажется, что дискриминант D = Ь2 - 4ас — отрица-
тельное число, то записанная формула не имеет смысла (под
знаком квадратного корня находится отрицательное число),
значит, корней нет. Если же окажется, что дискриминант равен
нулю, то получаем
_ -b±yfd __Ъ_
Xl-2 2а 2а'
т. е. один корень (говорят также, что квадратное уравнение в
= х2
= - —).
этом случае имеет два одинаковых корня: хх = х2
Наконец, если окажется, что Ъ2 - 4ас > 0, то получаются два
корня х1и х2, которые вычисляются по тем же формулам C), что
указаны выше.
Само число уЬ2-4ас в этом случае положительно (как
всякий квадратный корень из положительного числа), а двой-
ной знак перед ним означает, что в одном случае (при отыскании
х± ) это положительное число прибавляется к числу - Ъ, а в
другом случае (при отыскании х2) это положительное число вы-
читается из числа - Ъ.
У вас есть свобода выбора. Хотите —- решайте квадратное
уравнение подробно, используя сформулированное выше прави-
ло; хотите — запишите сразу формулу D) и с ее помощью делайте
необходимые выводы.
Пример 5. Решить уравнения:
2 5 7
б) З*2 - 0,2* + 2,77 = 0.
5 _7_ _
С. 1 О "»
Решение, а) Конечно, можно использовать формулы D)
2 5 7
или C), учитывая, что в данном случае а = ^ , b = ё . с = - — . Но
о О 12
зачем выполнять действия с дробями, когда проще и, главное,
приятнее иметь дело с целыми числами? Давайте освободимся
от знаменателей. Для этого нужно умножить обе части уравне-
ния на 12, т. е. на наименьший общий знаменатель дробей, слу-
жащих коэффициентами уравнения. Получим
откуда 8х2 + 10* - 7 = 0.
А теперь воспользуемся формулой D)
_ -10±N/l02-4.8(-7)
,и далее
•"-1,2
_ -10 + ^100 + 224 _ -lOf^/324 _ -10±18
16
-10+18 1
Значит, хг= ——— = ^, Х2 =
16
-10-18
16
7
4*
16 2' 2 16
б) Мы снова имеем уравнение с дробными коэффициентами:
а = 3, Ъ = - 0,2, с = 2,77. Умножим обе части уравнения на 100,
тогда получим уравнение с целыми коэффициентами:
300*2 - 20* + 277 = 0.
Далее воспользуемся формулой D):
_ 20±7202-4-300-277
Xl'2 2-300 "
Простая прикидка показывает, что дискриминант (подкорен-
ное выражение) — отрицательное число. Значит, уравнение не
имеет корней. <Ц
Пример 6. Решить уравнение 5*2 - 2 <Д5 * + 1 = 0.
Решение. Здесь, в отличие от предыдущего примера,
предпочтительнее действовать по правилу, а не по сокращенной
формуле D). Имеем а = 5, Ъ = -2^15, с = 1, D = Ъ2 - 4ас =
= (- 2 д/Гб J - 4 • 5 • 1 = 60 - 20 = 40. Так как D > 0, то квадратное
уравнение имеет два корня, которые будем искать по формулам C)
2а
2-5
10
10
х,=
2а
10
127
Пример 7. Решить уравнение
х2 - Bр
(р2+р-2) =
Решение. Это квадратное уравнение отли-
чается от всех рассмотренных до сих пор квадрат-
ных уравнений тем, что в роли коэффициентов
выступают не конкретные числа, а буквенные
выражения. Такие уравнения называют уравне-
ниями с буквенными коэффициентами или
уравнениями с параметрами. В данном случае
параметр (буква) р входит в состав второго ко-
эффициента и свободного члена уравнения.
Найдем дискриминант:
D = Bр + IJ - 4 • 1 • (р2 +р - 2) = Dр2 + 4р + 1) - Dр2 + 4р - 8) = 9.
параметр
уравнение
с параметром
Далее,
2(р + 2)
2р+1-3
О т в е т: р + 2; р - 1.
Пример 8. Решить уравнение
р*2 + A - р) х - 1 = 0.
Решение. Это также уравнение с параметром р, но, в отли-
чие от предыдущего примера, его нельзя сразу решать по
формулам D) или C). Дело в том, что указанные формулы
применимы к квадратным уравнениям, а про заданное уравнение
мы этого пока сказать не можем. В самом деле, а вдруг р = 0? Тогда
уравнение примет вид
О-*2+ A-0)*- 1 = 0,
т. е. х - 1 = 0, откуда получаем х = 1. Вот если точно известно,
что р Ф 0, то можно применять формулы корней квадратного
уравнения:
•"-1,2
128
2р
р-1±(р + 1)
4.21.
КВАДРАТНЫЕ УРАВНЕНИЯ
1
2р
_ 2р _ р-\-(р + \) -2
2р ' 2 2р 2р
Ответ: если р = 0, то х = 1; если р + 0, то хг = 1, х2 = - — .
125
Учебники и книги по всему предметам, домашняя работа, онлайн библиотеки книжек, планы конспектов уроков по математике, рефераты и конспекты уроков по математике для 8 класса скачать
Содержание урока
 конспект урока конспект урока
 опорный каркас опорный каркас
 презентация урока презентация урока
 акселеративные методы акселеративные методы
 интерактивные технологии
Практика интерактивные технологии
Практика
 задачи и упражнения задачи и упражнения
 самопроверка самопроверка
 практикумы, тренинги, кейсы, квесты практикумы, тренинги, кейсы, квесты
 домашние задания домашние задания
 дискуссионные вопросы дискуссионные вопросы
 риторические вопросы от учеников
Иллюстрации риторические вопросы от учеников
Иллюстрации
 аудио-, видеоклипы и мультимедиа аудио-, видеоклипы и мультимедиа
 фотографии, картинки фотографии, картинки
 графики, таблицы, схемы графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты
Дополнения притчи, поговорки, кроссворды, цитаты
Дополнения
 рефераты рефераты
 статьи статьи
 фишки для любознательных фишки для любознательных
 шпаргалки шпаргалки
 учебники основные и дополнительные учебники основные и дополнительные
 словарь терминов словарь терминов
 прочие
Совершенствование учебников и уроков прочие
Совершенствование учебников и уроков
 исправление ошибок в учебнике исправление ошибок в учебнике
 обновление фрагмента в учебнике обновление фрагмента в учебнике
 элементы новаторства на уроке элементы новаторства на уроке
 замена устаревших знаний новыми
Только для учителей замена устаревших знаний новыми
Только для учителей
 идеальные уроки идеальные уроки
 календарный план на год календарный план на год
 методические рекомендации методические рекомендации
 программы программы
 обсуждения
Интегрированные уроки обсуждения
Интегрированные уроки
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.
|