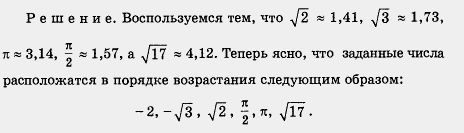Гипермаркет знаний>>Математика>>Математика 8 класс>>Математика:Множество действительных чисел

                                           МНОЖЕСТВО ДЕЙСТВИТЕЛЬНЫХ ЧИСЕЛ

Если множество рациональных чисел дополнить множеством иррациональных чисел, то вместе они составят множество действительных чисел. Множество действительных чисел обычно обозначают буквой R; используют также символическую запись (-оо, +оо) или (-оо, оо).

Множество действительных чисел можно описать так: это множество конечных и бесконечных десятичных дробей; конечные десятичные дроби и бесконечные десятичные периодические дроби — рациональные числа, а бесконечные десятичные непериодические дроби — иррациональные числа.

 Каждое действительное число можно изобразить точкой на координатной прямой. Верно и  обратное: каждая точка координатной прямой  имеет действительную координату. Математики обычно, говорят так: между множеством R действительных чисел и множеством точек координатной прямой установлено взаимно однозначное со ответствие. Координатная прямая есть геометрическая модель множества действительных чисел; по этой причине для координатной прямой часто используют термин числовая прямая.

Вдумайтесь в этот термин: не кажется ли он вам противоестественным? Ведь число — объект алгебры, а прямая — объект геометрии. Нет ли тут «смешения жанров»? Нет, все логично, все продумано. Этот термин в очередной раз подчеркивает единство различных областей математики, дает возможность
отождествления понятий «действительное число» и «точка на координатной (числовой) прямой».

Обратите внимание: координатной прямой вы пользовались начиная с 5-го класса. Но, оказывается, в ваших знаниях был вполне оправданный пробел: не для любой точки координатной прямой вы сумели бы найти координату — просто учитель оберегал вас от такой неприятности.

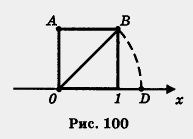
Рассмотрим пример. Дана координатная прямая, на ее единичном отрезке построен квадрат (рис. 100), диагональ квадрата ОВ отложена на координатной прямой от точки О вправо, получилась точка D. Чему равна координата точки D? Она равна длине диагонали квадрата, т. е. . Это число, как
мы теперь знаем, не целое и не дробь. Значит, ни в 5-м, ни в 6-м, ни в 7-м классе координату точки D вы бы найти не смогли.

Потому мы до сих пор и говорили «координатная прямая», а не «числовая прямая».

Заметим, что был еще один оправданный пробел в ваших знаниях по алгебре. Рассматривая выражения с переменными, мы всегда подразумевали, что переменные могут принимать любые допустимые значения, но только рациональные, ведь других-то не было. На самом деле переменные могут принимать
любые допустимые действительные значения. Например, в тождестве
(а + Ь){а-b) = а²-b² в роли а и b могут выступать любые числа, не обязательно
рациональные. Этим мы уже пользовались в конце предыдущего параграфа. Этим же мы пользовались и в § 18 — в частности, в примерах 6, 7, 8 из указанного параграфа.

Для действительных чисел а, b, с выполняются привычные законы:
а + b = b + а;
аЬ = bа;

a + (b + c) = (a + b) + c

a(bc) =(ab)c
(а + b) с = ас + bc и т. д.
Выполняются и привычные правила: произведение (частное) двух положительных чисел — положительное число;
произведение (частное) двух отрицательных чисел — положительное число;
произведение (частное) положительного и отрицательного числа — отрицательное число.

Действительные числа можно сравнивать друг с другом, используя следующее определение.

Определение. Говорят, что действительное число а больше (меньше) действительного числа b, если их разность а - b — положительное (отрицательное) число. Пишут а > b (а < b).

Из этого определения следует, что всякое положительное число а больше нуля (поскольку разность а - 0 = а — положительное число), а всякое отрицательное число b меньше нуля (поскольку разность b - 0 = b — отрицательное число).

Итак, а > 0 означает, что а — положительное число;
а < 0 означает, что а — отрицательное число;
а>b означает, что а -b — положительное число, т. е. а - b > 0;
a<b означает, что а - b — отрицательное число,
т.е. а - b < 0.
Наряду со знаками строгих неравенств (<, >) используют знаки нестрогих неравенств:
а 0 означает, что а больше нуля или равно нулю, т. е. а — неотрицательное число (положительное или 0), или что а не меньше нуля;
а 0 означает, что а меньше нуля или равно нулю, т. е. а — неположительное число (отрицательное или 0), или что а не больше нуля;
а b означает, что а больше или равно b, т. е. а - b — неотрицательное число, или что а не меньше b; а - b 0;
а b означает, что а меньше или равно b, т. е. а - b — неположительное число, или что а не больше Ь; а - b 0.
Например, для любого числа а верно неравенство а² 0;
для любых чисел а и b верно неравенство (а - b)² 0.
Впрочем, для сравнения действительных чисел необязательно каждый раз составлять их разность и выяснять, положительна она или отрицательна. Можно сделать соответствующий вывод, сравнивая записи чисел в виде десятичных дробей.

Геометрическая модель множества действительных чисел, т. е. числовая прямая, делает операцию сравнения чисел особенно наглядной: из двух чисел а, b больше то, которое располагается на числовой прямой правее.

Таким образом, к сравнению действительных чисел нужно подходить достаточно гибко, что мы и используем в следующем примере.

Пример 1. Сравнить числа:

Пример 2. Расположить в порядке возрастания числа

_{Планирование математике, материалы по математике 8 класса скачать, учебники онлайн}

Содержание урока
 конспект урока                       
 опорный каркас  
 презентация урока
 акселеративные методы 
 интерактивные технологии 

Практика
 задачи и упражнения 
 самопроверка
 практикумы, тренинги, кейсы, квесты
 домашние задания
 дискуссионные вопросы
 риторические вопросы от учеников
 
Иллюстрации
 аудио-, видеоклипы и мультимедиа 
 фотографии, картинки 
 графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты

Дополнения
 рефераты
 статьи 
 фишки для любознательных 
 шпаргалки 
 учебники основные и дополнительные
 словарь терминов                          
 прочие 

Совершенствование учебников и уроков
 исправление ошибок в учебнике
 обновление фрагмента в учебнике 
 элементы новаторства на уроке 
 замена устаревших знаний новыми 
 
Только для учителей
 идеальные уроки 
 календарный план на год  
 методические рекомендации  
 программы
 обсуждения


Интегрированные уроки

Если у вас есть исправления или предложения к данному уроку, напишите нам.

Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.