Гипермаркет знаний>>Математика>>Математика 5 класс>>Математика:Сложение натуральных чисел и его свойства

                                      Сложение натуральных чисел и его свойства

Если прибавить к натуральному числу единицу, то получится следующее за ним число. Например, 6+1= 7; 99 + 1 = 100.
 Сложить числа 5 и 3 — значит прибавить к числу 5 три раза единицу.
Получим: 5 + 3 = 5+1 + 1 + 1=6 + 1 + 1=7+1=8.
Пишут короче: 5 + 3 = 8.
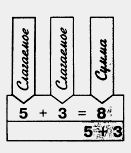
Числа, которые складывают, называют слагаемыми число, получающееся при сложении этих чисел, называют их суммой. В записи 5 + 3 = 8 числа 5 и 3 —
слагаемые, а число 8 — сумма.

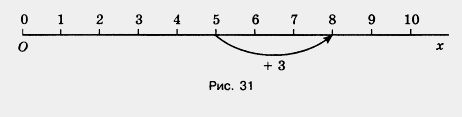
Сложение чисел можно изобразить на координатном луче (рис. 31).

Мы знаем следующие свойства сложения:

1. Сумма чисел не изменяется при перестановке слагаемых.
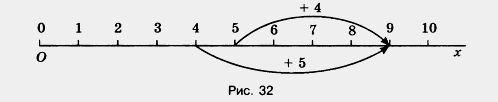
Например: 5 + 4 = 9 и 4 + 5 = 9.
Это свойство сложения называют переместительным (рис. 32).

2. Чтобы прибавить к числу сумму двух чисел, можно сначала прибавить I первое слагаемое, а потом к полученной сумме — второе слагаемое.
Например, 3 + (8 + 6) = 3 + 14 = 17 и (3 + 8) + 6 = 11 + 6 = 17.
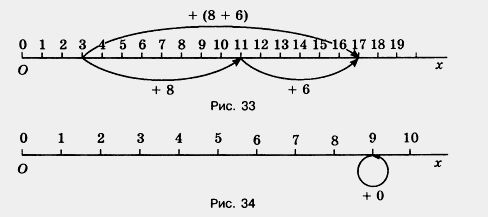
Это свойство сложения называют сочетательным (рис. 33).

3. От прибавления нуля число не изменяется.
Например, 9 + 0 = 9 (рис. 34). Так как 9 + 0 = 0 + 9, то и 0 + 9 = 9. Значит, I если прибавить к нулю какое-нибудь число, то получится прибавленное I число.
Вместо (5 + 9) + 7 пишут короче: 5 + 9 + 7. Когда в записи суммы нет скобок, то сложение выполняют по порядку слева направо.

Если точка С лежит на отрезке АВ, то длина всего отрезка АВ равна сумме  длин его частей АС и СВ.
Пишут: АВ = АС + СВ.
Сумму длин сторон многоугольника называют периметром этого многоугольника.
Если в треугольнике ABC АВ = 3 см, ВС = 4 см и СА = 5 см, то периметр треугольника ABC равен 3 + 4 + 5, то есть 12 см.

Какое число надо прибавить к натуральному числу, чтобы получилось следующее за ним число?
Какие числа называют слагаемыми?
Что называют суммой двух чисел?
Сформулируйте переместительное свойство сложения.
Сформулируйте сочетательное свойство сложения.
Изменяется ли число, если к нему прибавить нуль?
Чему равна сумма нуля и числа?
Что такое периметр треугольника?

182. Найдите суммы: 999 + 1; 78 099 + 1; 999 999 + 1.

183. Найдите сумму 76 + 24. Сколько единиц надо прибавить к числу 76, чтобы получить 100?

184. Купили 3 кг картофеля, 3 кг свеклы, 4 кг моркови, 5 кг яблок, 6 кг капусты, 2 кг груш и 4 кг слив. Сколько было куплено килограммов овощей и сколько килограммов фруктов?

185. Две девочки собирали в лесу малину. Первая девочка собрала 1 кг 250 г малины, а вторая — на 300 г больше. Сколько граммов малины собрали две девочки вместе?

186. В одной пачке 23 книги и в ней на 8 книг меньше, чем во второй, а в третьей пачке на 6 книг больше, чем во второй. Сколько всего книг в трех пачках?

187. В первый день собрали 127 т картофеля, что на 32 т меньше, чем во второй день. В третий день собрано на 40 т больше, чем в первый день. Сколько всего тонн картофеля было собрано за эти три дня?

188. Начертите координатный луч и отметьте на нем точку С(6), отложите от этой точки вправо 5 единичных отрезков и отметьте точку D. Чему равна координата точки D?

189. Начертите координатный луч и отметьте на нем точки М(7) и Г(15). Сколько единичных отрезков надо отложить от точки М и в какую сторону, чтобы попасть в точку Т?

190. Изобразите на координатном луче сложение:

4 + 3; 4 + 6;

4 + 8; 8 + 4.

191. Выполните действия:

а) (457 + 705) + 295;

б) 554 + (46 + 1425).

192. Вычислите сумму, выбирая удобный порядок выполнения действий:

а) 385 + 548 + 615;

б) 221 + 427 + 373.

193. Вычислите:
а) 458 + 333 + 42 + 67;
б) 635 + 308 + 1365 + 392;
в) 411 + 419 + 145 + 725 + 87;
г) 11 + 12 + 13 + 14 + 15 + 16 + 17 + 18 + 19.

194. Представление числа 8903 в виде суммы 8000 + 900 + 3 называют разложением этого числа по разрядам.

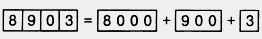
Разложите по разрядам числа:
48; 304;        57 608;        735 882;      4 308 001;       54 985 019 247.

195. Какое число разложили по разрядам:

а) 7 000 000 + 600 000 + 40 000 + 5000 + 300 + 20 + 7;
б) 4 000 000 000 + 5 000 000 + 4?

196. Выполните сложение:

а) 3 419 845 099 + 11 087 609 311;
б) 94 029 547 608 + 8 997 684 513;
в) 63 000 768 676 + 51 673 008;
г) 3 245 983 754 + 188 976 233 467.

197. Замените звездочки цифрами так, чтобы получились правильно выполненные примеры на сложение:

198. В таблице указана стоимость (в млн рублей) продукции мебельной фабрики за январь, февраль и март. Заполните пустые клетки таблицы:

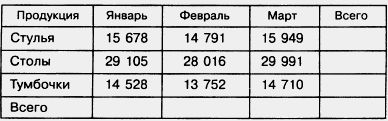
199. Заполните пустые клетки таблицы:

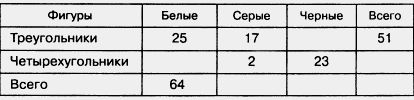
200. Какая из сумм 18 + 24 или 18 + 35 больше? Какая из сумм 18 4- 24 или 21 + 35 больше? Что происходит с суммой при увеличении слагаемых? А при их уменьшении?

201. Какая из сумм больше: 509 + 971 или 453 4- 872? Ответьте, не выполняя вычислений.

202. Не вычисляя, расположите суммы в порядке возрастания:

а) 78 + 65; г) 37 + 42;
б) 78 + 42; д) 144 + 83.
в) 144 + 65;

203. Докажите, что:

а) 5000 + 7000 < 5374 + 7980 < 6000 + 8000;
б) 17 000 < 6809 + 11 861 < 19 000.

204. Ученик, складывая числа 9875 и 6371, получил ответ 97 246. Каким путем он может сразу обнаружить свою ошибку?

205. Точка В делит отрезок АК на две части. Отрезок АВ равен 27 мм, а отрезок ВК на 30 мм длиннее отрезка АВ. Найдите длину отрезка АК.

206. Точки М и К делят отрезок АВ на три части: АМУ МК и КВ. Найдите длину отрезка АВУ если AM = 3 см 5 мм, отрезок МК на 13 мм длиннее отрезка AM, а отрезок АК на 8 мм короче отрезка КВ.

207. Длина прямоугольного садового участка 86 м, а ширина 9 м. Найдите длину забора этого участка.

208. Одна из сторон прямоугольника 24 см, а другая в 3 раза больше. Найдите периметр прямоугольника.

209. В треугольнике DKC сторона DK меньше стороны КС на 6 см и больше стороны DC на 2 см. Найдите периметр треугольника DKC, если DC = 18 см.

210. Начертите квадрат со стороной 3 см. Вычислите его периметр.

211. В четырехугольнике ABCD сторона AD на 4 см 6 мм больше стороны АВ> а АВ = ВС = CD = 13 см. Найдите периметр четырехугольника
ABCD.

212. Вычислите устно:

213. Выполните деление:
а) 1 т : 200 кг;                           в) 8 ц : 16 кг;
б) 1 км : 100 м;                         г) 36 км : 600 м.

214. Какое число стоит в конце цепочки?

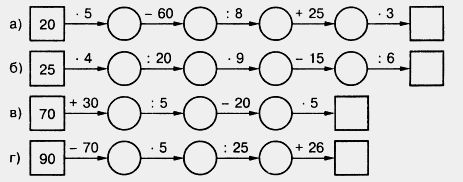
215. Из чисел, оканчивающихся цифрой 5, выпишите такие, которые боль-
ше 160, но меньше 200.
216. Город был основан 8 веков назад. Строительство крепости в городе
продолжалось пятую часть времени его существования. Сколько лет строи-
лась крепость?
217. Существует ли натуральное число, которое равно сумме всех пред-
шествующих ему натуральных чисел?
218. Как изменится двузначное число, если к нему приписать:
а) два нуля; б) такое же число?
219. Составьте условие задачи, которая решается с помощью выражения:
а) 120 + 35; б) 80 + 25 + 60; в) 140 - 50; г) 90 - 20 - 45.
220. Сравните числа, поставив вместо звездочки знак < или >:
375 * 383; 123 * 103; 3789 * 3798.
221. Выразите в килограммах: 3000 г; 15 000 г; 4 т; 17 ц.
222. Выразите в граммах: 5 кг 421 г; 6 ц 14 кг; 2 т 765 кг 123 г.
223. Начертите отрезок АВ длиной 7 см и отрезок CD, равный от-
резку АВ.
224. На шкале времени деления обозначают один век:
I п ш IV
н—i i i
v vi vii viii IX х xi хп xmxivxvxvixvnxvTnxixxxxxi
Н 1 I I I I I I I I I 1 > I I ! 1
Покажите на шкале:
а) начало и конец второго века;
б) конец шестого века;
в) седьмой век;
г) середину двенадцатого века;
д) первую половину семнадцатого века.
225. Сколько лет составляют два века? Полвека? Четверть века? Сколько
веков составляют 300 лет? 500 лет? 1000 лет?
226. Сравните числа и запишите результат с помощью знака < или знака >:
1) 800 106 и 98 004;
2) 706 051 и 3 300 011;
227. Выполните действия:
1) 256 + 44- (135 - 86);
2) 344 + 56 • (153 -95);
3)4 603 172 и 4 603 181;
4) 707 837 и 707 829.
3) (1239 + 601) • (1521 - 1481);
4) (1203 - 1143) • (1176 + 394).
228. Сколько трехзначных чисел можно составить из цифр 2, 4, 6, 8,
если цифры в записи числа не повторяются?
Решение. Первой цифрой числа может быть любая из четырех дан-
ных цифр, второй — любая из трех других, а третьей — любая из двух
оставшихся. Получается:
Первая цифра
Вторая цифра
Третья цифра
Всего из данных цифр можно составить 4 • 3 • 2 = 24 трехзначных числа.
229. Школьники трех классов помогали в уборке картофеля. Один
класс собрал 230 кг картофеля, другой — на 20 кг больше, чем первый,
но оба класса собрали вместе на 40 кг меньше, чем третий класс. Сколько
килограммов картофеля было собрано тремя классами?
230. Квартира состоит из трех комнат. Первая комната на 5 м2 меньше
второй, а вторая на 8 м2 меньше третьей. Найдите общую площадь трех
комнат, если площадь самой маленькой из них равна 10 м2.
231. Выполните действия, применяя сочетательное свойство сложения:
в) 19 999 + (4801 + 15 200);
г) 18 356 + (1644 + 2135).
а) (7357 + 2848) + 5152;
б) (54 271 + 39 999) + 10 001;
232. Разложите по разрядам число:
а) 7 008 001; б) 33 333.
233. Выполните сложение:
а) 5 387 284 367 + 21 542 357 285 + 3 070 358 347;
б) 278 504 247 961 + 33 869 029 453 + 87 696 632 596.
234. Вычислите стоимость товаров (в тыс. рублей), поступивших в от-
делы магазина за неделю. Такой же расчет сделайте по всему магазину.
Дни недели
Понедельник
Вторник
Среда
Четверг
Пятница
Суббота
Итого:
Отделы
Одежда
650
860
1320
870
1086
980
Обувь
450
511
802
360
987
564
Трикотаж
330
440
510
710
652
382
Всего по магазину
235. Найдите число, оканчивающееся цифрой 7, если оно:
а) больше 131 и меньше 141; б) меньше 457 и больше 437.
236. Найдите периметр треугольника КМР, если длина стороны КМ
равна 5 см 8 мм, сторона МР на 1 см 5 мм длиннее стороны КМ, но короче
на 2 см 3 мм стороны РК.
237. Длина прямоугольника 1 м 25 см, а ширина в 5 раз меньше. Най-
дите длину стороны квадрата, периметр которого равен периметру этого
прямоугольника.
238. За неделю собрали 6500 кг винограда, из которых 650 кг переда-
ли в детский сад, а остальной виноград отправили в город в ящиках.
Сколько ящиков с виноградом отправили в город, если в каждом ящике
было 13 кг винограда?
239. Отметьте на координатном луче все точки, координаты которых —
натуральные числа:
а) меньшие, чем 8;
б) меньшие, чем 15, но большие, чем 10.
240. Выполните действия:
а) (2928 - 88) : 142; г) 15 732 : 57 : (156 : 13);
б) (64 + 37) • 91; д) (880 + 230) • 54 : 37;
в) 1032 : (5472 : 19 : 12); е) (3211 + 103 • 23) : 124.
В старину в России применялись меры массы не такие, как в настоящее время.
Например, для взвешивания мелких, но дорогих товаров применялся золотник
(около 4 г), в торговле использовались фунт (1 фунт = 96 ъолотникйм), пуд (1 пуд =
= 40 фунтам), берковец [1 берковец = 10 пудЬм).
241. Составьте задачу с использованием старых русских мер массы.

Н.Я. ВИЛЕНКИН, B. И. ЖОХОВ, А. С. ЧЕСНОКОВ, C. И. ШВАРЦБУРД, Математика 5 класс, Учебник для общеобразовательных учреждений

_{Полный перечень тем по классам, календарный план согласно школьной программе по математике онлайн, видеоматериал по математике для 5 класса скачать}

Содержание урока
 конспект урока                       
 опорный каркас  
 презентация урока
 акселеративные методы 
 интерактивные технологии 

Практика
 задачи и упражнения 
 самопроверка
 практикумы, тренинги, кейсы, квесты
 домашние задания
 дискуссионные вопросы
 риторические вопросы от учеников
 
Иллюстрации
 аудио-, видеоклипы и мультимедиа 
 фотографии, картинки 
 графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты

Дополнения
 рефераты
 статьи 
 фишки для любознательных 
 шпаргалки 
 учебники основные и дополнительные
 словарь терминов                          
 прочие 

Совершенствование учебников и уроков
 исправление ошибок в учебнике
 обновление фрагмента в учебнике 
 элементы новаторства на уроке 
 замена устаревших знаний новыми 
 
Только для учителей
 идеальные уроки 
 календарный план на год  
 методические рекомендации  
 программы
 обсуждения


Интегрированные уроки

Если у вас есть исправления или предложения к данному уроку, напишите нам.

Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.