Гипермаркет знаний>>Математика>>Математика 8 класс>>Математика: Трапеция

                                                             ТРАПЕЦИЯ

Трапецией называется четырехугольник, у которого только две противолежащие стороны параллельны. Эти параллельные стороны называются основаниями трапеции. Две другие стороны называются боковыми сторонами.

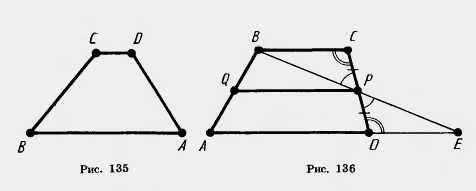
На рисунке 135 вы видите трапецию ABCD с основаниями АВ и CD и боковыми сторонами ВС и AD.

Трапеция, у которой боковые стороны равны, называется равнобокой. Отрезок, соединяющий середины боковых сторон, называется средней линией трапеции.

Теорема 6.8. Средняя линия трапеции параллельна основаниям и равна их полусумме.

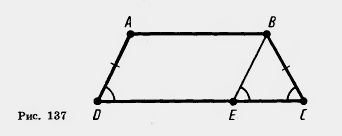
Доказательство. Пусть ABCD — данная трапеция (рис. 136). Проведем через вершину В и середину Р боковой стороны CD прямую. Она пересекает прямую AD в некоторой точке Е.

Треугольники РВС и PED равны по второму признаку равенства треугольников. У них CP=DP по построению, углы при вершине Р равны как вертикальные, а углы РСВ и PDE равны как внутренние накрест лежащие при параллельных прямых ВС и AD и секущей CD. Из равенства треугольников следует равенство сторон: РВ=РЕ, BC=ED.

Значит, средняя линия PQ трапеции является средней линией треугольника ABE. По свойству средней линии треугольника PQIIAE и отрезок

Теорема доказана.

Задача (60). Докажите, что у равнобокой трапеции углы при основании равны.

Решение. Пусть ABCD — равнобокая трапеция (рис. 137). Докажем, что углы трапеции при основании CD равны.


 
Проведем через вершину В прямую, параллельную стороне AD. Она пересечет луч DC в некоторой точке Е. Четырехугольник ABED — параллелограмм. По свойству параллелограмма BE=AD. По условию AD=BC (трапеция равнобокая), значит, треугольник ВСЕ равнобедренный с основанием ЕС. Углы треугольника и трапеции при вершине С совпадают, а углы при вершинах Е и D равны как соответственные углы при пересечении параллельных прямых секущей. Поэтому ADC= BCD. Утверждение доказано.
 

А. В. Погорелов, Геометрия для 7-11 классов, Учебник для общеобразовательных учреждений

_{Видео по математикескачать, домашнее задание, учителям и школьникам на помощь онлайн}

Содержание урока
 конспект урока                       
 опорный каркас  
 презентация урока
 акселеративные методы 
 интерактивные технологии 

Практика
 задачи и упражнения 
 самопроверка
 практикумы, тренинги, кейсы, квесты
 домашние задания
 дискуссионные вопросы
 риторические вопросы от учеников
 
Иллюстрации
 аудио-, видеоклипы и мультимедиа 
 фотографии, картинки 
 графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты

Дополнения
 рефераты
 статьи 
 фишки для любознательных 
 шпаргалки 
 учебники основные и дополнительные
 словарь терминов                          
 прочие 

Совершенствование учебников и уроков
 исправление ошибок в учебнике
 обновление фрагмента в учебнике 
 элементы новаторства на уроке 
 замена устаревших знаний новыми 
 
Только для учителей
 идеальные уроки 
 календарный план на год  
 методические рекомендации  
 программы
 обсуждения


Интегрированные уроки

Если у вас есть исправления или предложения к данному уроку, напишите нам.

Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.