Гипермаркет знаний>>Математика>>Математика 8 класс>>Математика: Неравенство треугольника

                                 НЕРАВЕНСТВО ТРЕУГОЛЬНИКА

Если точки А и В различны, то расстоянием между ними называется длина отрезка АВ. Если точки А и B совпадают, то расстояние между ними принимается равным нулю.

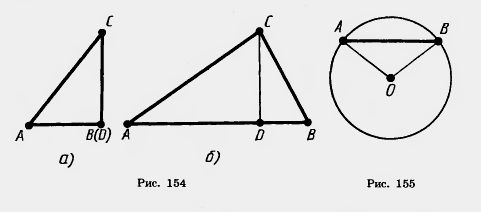
Теорема 7.3 (неравенство треугольника). Каковы бы ни были три точки, расстояние между любыми двумя из этих точек не больше суммы расстояний от них до третьей точки.

Это значит, что каждое из этих расстояний меньше суммы или равно сумме двух других.

Доказательство. Пусть А, В, С — три данные точки. Если две точки из трех или все три точки совпадают, то утверждение теоремы очевидно.

Если все точки различны и лежат на одной прямой, то одна из них лежит между двумя другими, например В. В этом случае АВ + ВС = АС. Отсюда видно, что каждое из трех расстояний не больше суммы двух других.

Допустим теперь, что точки не лежат на одной прямой (рис. 154). Докажем, что АВ<АС + ВС. Опустим перпендикуляр CD на прямую АВ. По доказанному ABAD + BD. И так как AD<AC и BD<BC, то АВ<АС+ВС. Теорема доказана.
 


Заметим, что в случае, когда точки не лежат на одной прямой, в неравенстве треугольника строгое неравенство. Отсюда следует, что в любом треугольнике каждая сторона меньше суммы двух других сторон.

Задача (23). Докажите, что любая хорда окружности не больше диаметра и равна диаметру только тогда, когда сама является диаметром.

Решение (рис. 155). По неравенству треугольника ABOA + OB = 2R, причем если центр О не лежит на отрезке АВ, то неравенство строгое. Равенство имеет место только в случае, когда хорда проходит через центр, т. е. является диаметром.

А. В. Погорелов, Геометрия для 7-11 классов, Учебник для общеобразовательных учреждений

_{Рефераты, домашняя работа по математике скачать, учебники скатать бесплатно, онлайн уроки, вопросы и ответы}

Содержание урока
 конспект урока                       
 опорный каркас  
 презентация урока
 акселеративные методы 
 интерактивные технологии 

Практика
 задачи и упражнения 
 самопроверка
 практикумы, тренинги, кейсы, квесты
 домашние задания
 дискуссионные вопросы
 риторические вопросы от учеников
 
Иллюстрации
 аудио-, видеоклипы и мультимедиа 
 фотографии, картинки 
 графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты

Дополнения
 рефераты
 статьи 
 фишки для любознательных 
 шпаргалки 
 учебники основные и дополнительные
 словарь терминов                          
 прочие 

Совершенствование учебников и уроков
 исправление ошибок в учебнике
 обновление фрагмента в учебнике 
 элементы новаторства на уроке 
 замена устаревших знаний новыми 
 
Только для учителей
 идеальные уроки 
 календарный план на год  
 методические рекомендации  
 программы
 обсуждения


Интегрированные уроки

Если у вас есть исправления или предложения к данному уроку, напишите нам.

Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.