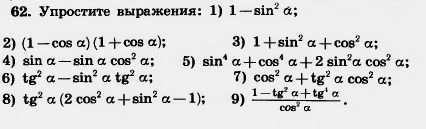Гипермаркет знаний>>Математика>>Математика 8 класс>>Математика: Задачи-2(8 класс)

                                              ЗАДАЧИ
 

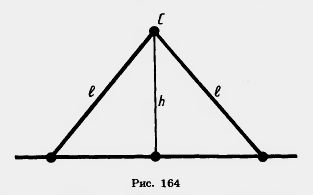
1.    Постройте угол, косинус которого равен: 3) 0,5; 4) 0,8.

2.    У прямоугольного треугольника заданы катеты а и b. Найдите гипотенузу, если: 1) а=3, b = 4; 2) а=1, b = 1; 3) а=5, b = 6.

3.    У прямоугольного треугольника заданы гипотенуза с и катет а. Найдите второй катет, если:

1) с = 5, а = 3; 2) с = 13, а = 5; 3) с = 6, а=5.

4.    Две стороны прямоугольного треугольника равны 3 м и 4 м. Найдите третью сторону. (Два случая.)

5.    Могут ли стороны прямоугольного треугольника быть пропорциональны числам 5, 6, 7?
6.    Найдите сторону ромба, если его диагонали равны: 1) 6 см и 8 см; 2) 16 дм и 30 дм; 3) 5 м и 12 м.

7.    Стороны прямоугольника 60 см и 91 см. Чему равна диагональ?

8.    Диагональ квадрата а. Чему равна сторона квадрата?

9.    Можно ли из круглого листа железа диаметром 1,4 м вырезать квадрат со стороной 1 м?

10.    Найдите высоту равнобокой трапеции, у которой основания 5 м и 11 м, а боковая сторона 4 м.

11.    Найдите медиану равнобедренного треугольника с основанием а и боковой стороной Ь, проведенную к основанию.

12.    Могут ли увидеть друг друга космонавты, летящие над поверхностью Земли на высоте 230 км, если расстояние между ними по прямой равно 2200 км? Радиус Земли равен 6370 км.

13.    В равностороннем треугольнике со стороной а найдите высоту.

14.    Даны отрезки а и b. Как построить отрезок: 1) 2)

15*. Даны отрезки а и b. Как построить отрезок ?
16. Между двумя фабричными зданиями устроен покатый желоб для передачи материалов. Расстояние между зданиями равно 10 м, а концы желоба расположены на высоте 8 м и 4 м над землей. Найдите длину желоба.

17.    Докажите, что если треугольник имеет стороны а, b, с и а² +Ь² = с², то у него угол, противолежащий стороне с, прямой.

18.    Чему равен угол треугольника со сторонами 5, 12, 13, противолежащий стороне 13?

19. На стороне АВ треугольника ABC взята точка X.  Докажите, что отрезок СХ меньше по крайней мере одной из сторон АС или ВС.
20.    Докажите, что расстояние между любыми двумя точками на сторонах треугольника не больше большей из его сторон.

21.    Даны прямая и точка С на расстоянии h от этой прямой. Докажите, что из точки С можно провести две и только две наклонные длины I, если l>h (рис. 164).

22*. Докажите, что прямая, отстоящая от центра окружности на расстояние, меньшее радиуса, пересекает окружность в двух точках.

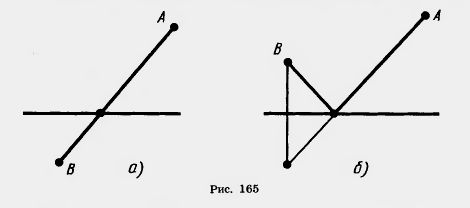
23. Докажите, что любая хорда окружности не больше диаметра и равна диаметру только тогда, когда сама является диаметром.

24.    Докажите, что точки А, В, С лежат на одной прямой, если:

1) АВ=b м, ВС = 7 м, АС = 12 м;

2) АВ=10,7, ВС = 17,1, АС=6,4.

25.    Докажите, что любая сторона треугольника больше разности двух других его сторон.

26.    Может ли у параллелограмма со сторонами 4 см и 7 см одна из диагоналей быть равной 2 см?

27.    В треугольнике одна сторона равна 1,9 м, а другая — 0,7 м. Найдите третью сторону, зная, что ее длина равна целому числу метров.

28*. Докажите, что медиана треугольника ABC, проведенная из вершины А, меньше полусуммы сторон АВ и АС.

29*. Известно, что диагонали четырехугольника пересекаются. Докажите, что сумма их длин меньше периметра, но больше полупериметра четырехугольника.

30. Отрезки АВ и CD пересекаются в точке О. Докажите, что сумма расстояний от любой точки плоскости до точек А, В, С и D не меньше,чем OA+OB+OC+OD.
31*. На прямолинейном шоссе требуется указать место автобусной остановки так, чтобы сумма расстояний от нее до населенных пунктов А и В была наименьшей. Рассмотрите два случая:

1) населенные пункты расположены по разные стороны от шоссе (рис. 165, а);

2) населенные пункты расположены по одну сторону от шоссе (рис. 165, б).

32.    Могут ли стороны треугольника быть пропорциональными числам 1, 2, 3?

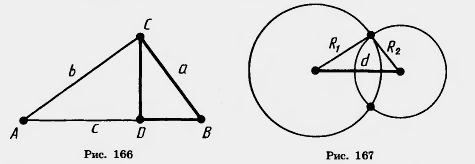
33.    Докажите, что в треугольнике каждая сторона меньше половины периметра.

34.    Внутри окружности радиуса R взята точка на расстоянии d от центра. Найдите наибольшее и наименьшее расстояния от этой точки до точек окружности

35.    Вне окружности радиуса R взята точка на расстоянии d от центра. Найдите наибольшее и наименьшее расстояния от этой точки до точек окружности.

36.    Могут ли пересекаться окружности, центры которых находятся на расстоянии 20 см, а радиусы 8 см и 11 см? Объясните ответ.

37.    Могут ли пересекаться окружности, центры которых находятся на расстоянии 5 см, а радиусы 6 см и 12 см? Объясните ответ.

38*. Докажите, что в задаче 36 окружности находятся одна вне другой, а в задаче 37 окружность радиуса 6 см находится внутри окружности радиуса 12 см.

39. Могут ли пересекаться окружности с радиусами R₁ и В₂ и расстоянием между центрами d, если R₁+R₂<d?

40*. Даны три положительных числа о, Ь, с, удовлетворяющие условиям . Докажите последовательно утверждения:

2) существует прямоугольный треугольник BCD, у которого гипотенуза ВС=а, а катет BD =  (рис. 166);
3) треугольник ABC, у которого ВС = а, АВ=с, а расстояние BD равно  , имеет сторону АС=b (рис. 166).
41.    Даны три положительных числа a, b, с. Докажите, что если каждое из этих чисел меньше суммы двух других, то существует треугольник со сторонами a, b, с.

42.    Можно ли построить треугольник со сторонами:
1) a= 1 см, b = 2 см, с=3 см;

2) a = 2 см, b = 3 см, с=4 см;

3) a = 3 см, b=7 см, с=11 см;

4) a = 4 см, b = 5 см, с = 9 см?

43*. Даны две окружности с радиусами R₁, R₂ и расстоянием между центрами d. Докажите, что если каждое из чисел R\, R2 и d меньше суммы двух других сторон, то окружности пересекаются в двух точках (рис. 167).

 
44. У прямоугольного треугольника один катет равен 8 см, а синус противолежащего ему угла равен 0,8. Найдите гипотенузу и второй катет.

45.    В прямоугольном треугольнике гипотенуза равна а, а один из острых углов а. Найдите второй острый угол и катеты.

46.    В прямоугольном треугольнике катет равен а, а противолежащий ему угол а. Найдите второй острый угол, противолежащий ему катет и гипотенузу.

47.    В прямоугольном треугольнике даны гипотенуза с и острый угол а. Найдите катеты, их проекции на гипотенузу и высоту, опущенную на гипотенузу.

48.    1) Найдите sin 22°; sin 22°36'; sin22°38'; sin 22°41' cos 68°; cos 68°18'; cos 68°23'.
        2) Найдите угол x, если sin x = 0,2850; sin x = 0,2844 cos л: = 0,2710.

49.    Найдите значения синуса и косинуса углов: 

  1)  16 2) 24°36'; 3) 70°32'; 4) 88°49'.

50.    Найдите величину острого угла х, если:

1) sin x = 0,0175
2)    sinx = 0,5015;

3) cos x = 0,6814;

4) cos x = 0,0670.

51.    Найдите значение тангенса угла:

   1)  10°;  2) 40°40' 3)    50°30'; 4) 70°15'.

52.    Найдите острый угол х, если:

1) tgx = 0,3227;

2) tg х = = 0,7846;

3) tgx = 6,152;

4) tgx = 9,254.

53.    Высота равнобедренного треугольника равна 12,4 м, а основание 40,6 м. Найдите углы треугольника и боковую сторону.

54.    Отношение катетов прямоугольного треугольника равно 19:28. Найдите его углы.

55.    Стороны прямоугольника равны 12,4 и 26. Найдите угол между диагоналями.

56.    Диагонали ромба равны 4,73 и 2,94. Найдите его углы.

57.    Сторона ромба 241 м, высота 120 м. Найдите углы.

58.    Радиус окружности равен 5 м. Из точки, отстоящей от центра на 13 м, проведены касательные к окружности. Найдите длины касательных и угол между ними.

59.    Тень от вертикально стоящего шеста, высота которого 7 м, составляет 4 м. Выразите в градусах высоту солнца над горизонтом (рис. 168).

60.    Основание равнобедренного прямоугольного треугольника равно о. Найдите боковую сторону.

61.    Найдите неизвестные стороны и острые углы прямоугольного треугольника по следующим данным:
1)    по двум катетам: а)a = 3, b = 4; б) a = 9, b = 40; в) a = 20, b = 21; г) a = 11, b = 60;
2)    по гипотенузе и катету: а) с=13, a = 5; б) с = 25, a = 7; в) с=17, a = 8; г) с=85, a = 84;
3)    по гипотенузе и острому углу: а) с=2, а = 20°; б) с = 4, а = 50°20'; в) с=8, а = 70°36'; г) с=16, а = 76°21';
4)    по катету и противолежащему углу: а) а = 3, а = 30°27'; б) a = 5, а = 40°48'; в) a = 7, а = 60°35'; г) a = 9, а = 68°.

63.    Вычислите значения sin а и tg а, если:
1) cosa=^;   2) cosa=i|;   3) cosa = 0,6.
lo    17
64.    Найдите cos a и tg a, если:
1) sina = -|-;   2)sina=^;   3)sina = 0,8.
65.    Постройте угол a, если известно, что:  1) cosa=-|-;
2)sina=^;  3)sina = 0,5;  4)tga=-|-;  5)tga = 0,7.
69
66. В прямоугольном треугольнике с гипотенузой а и углом 60° найдите катет, противолежащий этому углу.
67.    Найдите радиус г окружности, вписанной в равносторонний треугольник со стороной о, и радиус R окружности, описанной около него.
68.    В треугольнике один из углов при основании равен 45°, а высота делит основание на части 20 см и 21 см. Найдите большую боковую сторону' (рис. 169).
 

/
 
 
Рис. 168    Рис. 169
69.    У треугольника одна из сторон равна 1 м, а прилежащие к ней углы равны 30° и 45°. Найдите другие стороны треугольника.
70.    Диагональ прямоугольника в два раза больше одной из его сторон. Найдите углы между диагоналями.
71.    Диагонали ромба равны о и а V3. Найдите углы ромба.
У0 I  72. Какой из углов больше — а или р, если:
11    2    3
l)sina=-g-»   sinP=-^;     2)sina=-g-,     sinp=-j-;
3) cosa=-^,   cosP=-g-;    4) cosa = 0,75,   cos p = 0,74;
5)tga = 2,l,    tgp = 2,5;     6)tga=4-'      tgP=-|-?
' Иногда в произвольном треугольнике, необязательно равнобедренном, сторона, проведенная горизонтально, называется основанием, а две другие — боковыми сторонами, как в данной задаче.
73.    У прямоугольного треугольника ABC угол А больше угла В. Какой из катетов больше — АС или ВС?
74.    У прямоугольного треугольника ABC катет ВС больше катета АС. Какой угол больше — А или В?


 

А. В. Погорелов, Геометрия для 7-11 классов, Учебник для общеобразовательных учреждений

_{Материалы по математике онлайн, задачи и ответы по классам, планы конспектов уроков по математике скачать}

Содержание урока
 конспект урока                       
 опорный каркас  
 презентация урока
 акселеративные методы 
 интерактивные технологии 

Практика
 задачи и упражнения 
 самопроверка
 практикумы, тренинги, кейсы, квесты
 домашние задания
 дискуссионные вопросы
 риторические вопросы от учеников
 
Иллюстрации
 аудио-, видеоклипы и мультимедиа 
 фотографии, картинки 
 графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты

Дополнения
 рефераты
 статьи 
 фишки для любознательных 
 шпаргалки 
 учебники основные и дополнительные
 словарь терминов                          
 прочие 

Совершенствование учебников и уроков
 исправление ошибок в учебнике
 обновление фрагмента в учебнике 
 элементы новаторства на уроке 
 замена устаревших знаний новыми 
 
Только для учителей
 идеальные уроки 
 календарный план на год  
 методические рекомендации  
 программы
 обсуждения


Интегрированные уроки

Если у вас есть исправления или предложения к данному уроку, напишите нам.

Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.