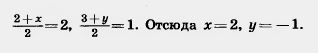Гипермаркет знаний>>Математика>>Математика 8 класс>>Математика: Координаты середины отрезка

                                       КООРДИНАТЫ СЕРЕДИНЫ ОТРЕЗКА

Пусть А(Х₁; у₁) и В(х₂; у₂) — две произвольные точки и С (х; у) — середина отрезка АВ. Найдем координаты х, у точки С.

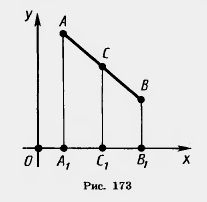
Рассмотрим сначала случай, когда отрезок АВ не параллелен оси у, т. е. Х₁Х₂. Проведем через точки А, В, С прямые, параллельные оси у (рис. 173). Они пересекут ось х в точках A₁(X₁; 0), B₁ (X₂; 0), C₁(х; 0). По теореме Фалеса точка С₁ будет серединой отрезка A₁B₁.

Так как точка С₁ —середина отрезка AiBi, то A₁C₁=B₁C₁, а значит, Ix — X₁I = Iх — Х₂I. Отсюда следует, что либо x —x₁ = x — x₂,    либо    (x — x₁) = —(x-x₂).
Первое равенство невозможно, так как x₁x₂. Поэтому верно второе. А из него получается формула

Если x₁=x₂, т. е. отрезок АВ параллелен оси у, то все три точки A₁, B₁, C₁ имеют одну и ту же   абсциссу. Значит, формула остается верной и в этом случае.
Ордината точки С находится аналогично. Через точки А, В, С проводятся прямые, параллельные оси х. Получается формула

Задача (15). Даны три вершины параллелограмма ABCD: А (1; 0), В (2; 3), С (3; 2). Найдите координаты четвертой вершины D и точки пересечения диагоналей.

Решение. Точка пересечения диагоналей является серединой каждой из них. Поэтому она является серединой отрезка АС, a значит, имеет координаты

 
Теперь, зная координаты точки пересечения диагоналей, находим координаты х, у четвертой вершины D. Пользуясь тем, что точка пересечения диагоналей является серединой отрезка BD, имеем:

А. В. Погорелов, Геометрия для 7-11 классов, Учебник для общеобразовательных учреждений

_{Планирование уроков по математике онлайн, задачи и ответы по классам, домашнее задание по математике 8 класса скачать}

Содержание урока
 конспект урока                       
 опорный каркас  
 презентация урока
 акселеративные методы 
 интерактивные технологии 

Практика
 задачи и упражнения 
 самопроверка
 практикумы, тренинги, кейсы, квесты
 домашние задания
 дискуссионные вопросы
 риторические вопросы от учеников
 
Иллюстрации
 аудио-, видеоклипы и мультимедиа 
 фотографии, картинки 
 графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты

Дополнения
 рефераты
 статьи 
 фишки для любознательных 
 шпаргалки 
 учебники основные и дополнительные
 словарь терминов                          
 прочие 

Совершенствование учебников и уроков
 исправление ошибок в учебнике
 обновление фрагмента в учебнике 
 элементы новаторства на уроке 
 замена устаревших знаний новыми 
 
Только для учителей
 идеальные уроки 
 календарный план на год  
 методические рекомендации  
 программы
 обсуждения


Интегрированные уроки

Если у вас есть исправления или предложения к данному уроку, напишите нам.

Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.