'Гипермаркет знаний>>Математика>>Математика 8 класс>>Математика: Уравнение прямой

                                         УРАВНЕНИЕ ПРЯМОЙ

Докажем, что любая прямая в декартовых координатах х, у имеет уравнение вида
ах + bу+с=0,    (*)
где а,b, с — некоторые числа, причем хотя бы одно из чисел а, b не равно нулю.

Пусть h — произвольная прямая на плоскости ху. Проведем какую-нибудь прямую,  перпендикулярную прямой  h  и отложим на ней от точки пересечения С с прямой h равные отрезки СА₁ и CA₂ (рис. 176).

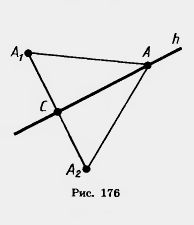
Пусть С|, Ъ\ — координаты точки А. i и 02, Ъг — координаты точки Аъ Как мы знаем, любая точка А {х; у) прямой ft равноудалена от точек А\ и А^. Поэтому координаты ее удовлетворяют уравнению
(x-a,f + (y~b,f = =(x-a2f + (y-bof.      I**)
Обратно: если координаты х и у какой-нибудь точки удовлетворяют уравнению (**), то эта точка равноудалена от точек Ai и А2, а значит, принадлежит прямой h. Таким образом, уравнение (**) является уравнением прямой h. Если в этом уравнении раскрыть скобки и перенести все члены уравнения в левую его часть, то оно примет вид:
2(02 —a,)x + 2(b2 —b,)y+(o? + bf—о|—bi)==0.
Обозначая 2(с2 —Oi)=o, 2{b2 — b,) = b, о? + b, — oi —b2 = c, получаем уравнение (*). По крайней мере одно из чисел о, b не равно нулю, так как точки А, и А2 различны. Утверждение доказано.
Задача (35). Составьте уравнение прямой, которая проходит через точки А{ — 1; 1), В(1; 0).
Решение. Как мы знаем, наша прямая имеет уравнение вида ах-\-Ьу-\-с=0. Точки А и В лежат на прямой, а значит, их координаты удовлетворяют этому уравнению.
Подставляя координаты точек А к В в уравнение прямой, получим:
—а + Ь + с=0, а + с=0.
Из этих уравнений можно выразить два коэффициента, например о и Ь, через третий: а = — с, Ь = —2с. Подставляя эти значения с и b в уравнение прямой, получим:
— сх — 2су-\-с=0.

На с можно сократить. Тогда получим:
-х-2у + 1=0. Это и есть уравнение нашей прямой.

 

А. В. Погорелов, Геометрия для 7-11 классов, Учебник для общеобразовательных учреждений

_{Полный перечень тем по классам, календарный план согласно школьной программе по математике онлайн, видеоматериал по математике для 8 класса скачать}

Содержание урока
 конспект урока                       
 опорный каркас  
 презентация урока
 акселеративные методы 
 интерактивные технологии 

Практика
 задачи и упражнения 
 самопроверка
 практикумы, тренинги, кейсы, квесты
 домашние задания
 дискуссионные вопросы
 риторические вопросы от учеников
 
Иллюстрации
 аудио-, видеоклипы и мультимедиа 
 фотографии, картинки 
 графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты

Дополнения
 рефераты
 статьи 
 фишки для любознательных 
 шпаргалки 
 учебники основные и дополнительные
 словарь терминов                          
 прочие 

Совершенствование учебников и уроков
 исправление ошибок в учебнике
 обновление фрагмента в учебнике 
 элементы новаторства на уроке 
 замена устаревших знаний новыми 
 
Только для учителей
 идеальные уроки 
 календарный план на год  
 методические рекомендации  
 программы
 обсуждения


Интегрированные уроки

Если у вас есть исправления или предложения к данному уроку, напишите нам.

Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.