Гипермаркет знаний>>Математика>>Математика 8 класс>>Математика: Пересечение прямой с окружностью

                                                ПЕРЕСЕЧЕНИЕ ПРЯМОЙ С ОКРУЖНОСТЬЮ

Рассмотрим вопрос о пересечении прямой с окружностью.

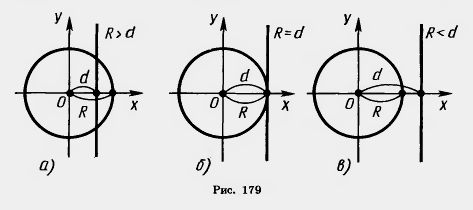
Пусть R — радиус окружности и d — расстояние от центра окружности до прямой. Примем центр окружности за начало координат, а прямую, перпендикулярную к данной, за ось х (рис. 179). Тогда уравнением окружности будет x'² + y²=R², а уравнением прямой x = d.

Для того чтобы прямая и окружность пересекались, надо, чтобы система двух уравнений

x'² + y²=R², x = d

имела решение. И обратно: всякое решение этой системы дает координаты X, у точки пересечения прямой с окружностью. Решая нашу систему, получим:

 
 
Из выражения для у видно, что система имеет два решения, т. е. окружность и прямая имеют две точки пересечения, если R>d (рис. 179,а).

Система имеет одно решение, если R=d (рис.  179,в).

В этом случае прямая и окружность касаются.

Система не имеет решения, т. е. прямая и окружность не пересекаются, если R<.d (рис. 179, в).

Задача (50). Найдите точки пересечения окружности х^ + у' = 1 с прямой J/ = 2JC-1-1.
Решение. Так как точки пересечения лежат на окружности и на прямой, то их координаты удовлетворяют системе уравнений

х² + у² = 1, y = 2х+1.

Решим эту систему. Подставим у из второго уравнения в первое. Получим уравнение для х:

5x² + 4x = 0.

Уравнение имеет два корня x₁ = 0 и. Это абсциссы точек пересечения. Ординаты этих точек получим из уравнения прямой, подставляя в него x₁ и x₂.

Получаем

y₁ = l, Итак, точки пересечения прямой и ок-ружности (0; 1) и .



 

А. В. Погорелов, Геометрия для 7-11 классов, Учебник для общеобразовательных учреждений

_{Сборник конспектов уроков по математике скачать, календарно-тематическое планирование, учебники по всем предметам онлайн}

Содержание урока
 конспект урока                       
 опорный каркас  
 презентация урока
 акселеративные методы 
 интерактивные технологии 

Практика
 задачи и упражнения 
 самопроверка
 практикумы, тренинги, кейсы, квесты
 домашние задания
 дискуссионные вопросы
 риторические вопросы от учеников
 
Иллюстрации
 аудио-, видеоклипы и мультимедиа 
 фотографии, картинки 
 графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты

Дополнения
 рефераты
 статьи 
 фишки для любознательных 
 шпаргалки 
 учебники основные и дополнительные
 словарь терминов                          
 прочие 

Совершенствование учебников и уроков
 исправление ошибок в учебнике
 обновление фрагмента в учебнике 
 элементы новаторства на уроке 
 замена устаревших знаний новыми 
 
Только для учителей
 идеальные уроки 
 календарный план на год  
 методические рекомендации  
 программы
 обсуждения


Интегрированные уроки

Если у вас есть исправления или предложения к данному уроку, напишите нам.

Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.