Гипермаркет знаний>>Математика>>Математика 8 класс>>Математика: Преобразования фигур

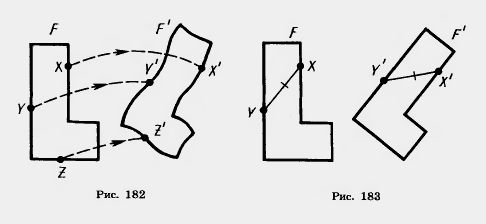
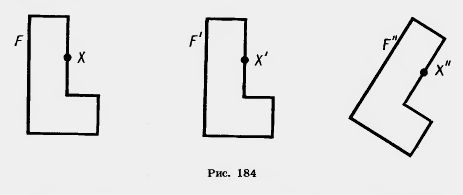
                                                     ПРЕОБРАЗОВАНИЯ ФИГУР

Если каждую точку данной фигуры сместить каким-нибудь образом, то мы получим новую фигуру. Говорят, что эта фигура получена преобразованием из данной (рис. 182).

Преобразование одной фигуры в другую называется движением, если оно сохраняет расстояние между точками, т. е. переводит любые две точки X и У одной фигуры в точки X', У другой фигуры так, что XY=X'Y' (рис. 183).

Замечание. Понятие движения в геометрии связано с обычным представлением о перемещении. Но если, говоря о перемещении, мы представляем себе непрерывный процесс, то в геометрии для нас будут иметь значение только начальное и конечное положения фигуры.
 

 

 
Пусть фигура F переводится движением в фигуру F', а фигура F' переводится движением в фигуру F" (рис. 184). Пусть при первом движении точка X фигуры F переходит в точку X' фигуры F', а при втором движении точка X' фигуры F' переходит в точку X" фигуры F". Тогда преобразование фигуры F в фигуру F", при котором произвольная точка X фигуры F переходит в точку X" фигуры F", сохраняет расстояние между точками, а значит, также является движением.

Это свойство движения выражают словами: два движения, выполненные последовательно, дают снова движение.

Пусть преобразование фигуры F в фигуру F' переводит различные точки фигуры F в различные точки фигуры F' (см. рис. 182). Пусть произвольная точка X фигуры F при этом преобразовании переходит в точку X' фигуры F'. Преобразование фигуры F' в фигуру F, при котором точка X' переходит в точку X, называется преобразованием, обратным данному. Движение сохраняет расстояние между точками, поэтому переводит различные точки в различные.

Очевидно, преобразование, обратное движению, также является движением.

А. В. Погорелов, Геометрия для 7-11 классов, Учебник для общеобразовательных учреждений

_{Книги и учебники согласно календарному плануванння по математике 8 класса скачать, помощь школьнику онлайн}

Содержание урока
 конспект урока                       
 опорный каркас  
 презентация урока
 акселеративные методы 
 интерактивные технологии 

Практика
 задачи и упражнения 
 самопроверка
 практикумы, тренинги, кейсы, квесты
 домашние задания
 дискуссионные вопросы
 риторические вопросы от учеников
 
Иллюстрации
 аудио-, видеоклипы и мультимедиа 
 фотографии, картинки 
 графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты

Дополнения
 рефераты
 статьи 
 фишки для любознательных 
 шпаргалки 
 учебники основные и дополнительные
 словарь терминов                          
 прочие 

Совершенствование учебников и уроков
 исправление ошибок в учебнике
 обновление фрагмента в учебнике 
 элементы новаторства на уроке 
 замена устаревших знаний новыми 
 
Только для учителей
 идеальные уроки 
 календарный план на год  
 методические рекомендации  
 программы
 обсуждения


Интегрированные уроки

Если у вас есть исправления или предложения к данному уроку, напишите нам.

Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.