Гипермаркет знаний>>Математика>>Математика 8 класс>>Математика: Свойства движения

                                    СВОЙСТВА ДВИЖЕНИЯ

Теорема 9.1. Точки, лежащие на прямой, при движении переходят в точки, лежащие на прямой, и сохраняется порядок их взаимного расположения.

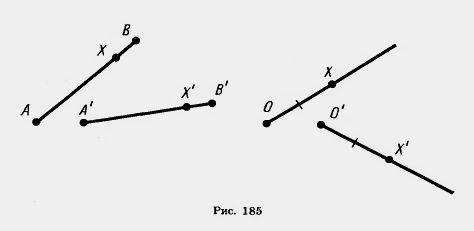
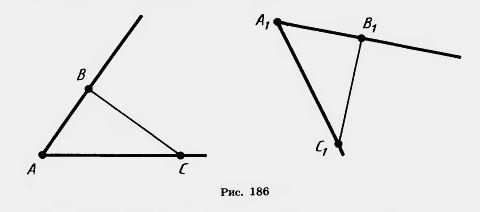
Это значит, что если точки А, В, С, лежащие на прямой, переходят в точки A₁, В₁, С₁, то эти точки также лежат на прямой;  если точка В лежит между точками А и С, то точка В₁ лежит между точками А₁ и C₁.

Доказательство. Пусть точка В прямой АС лежит между точками A и С. Докажем, что точки A₁, В₁, С₁ лежат на одной прямой.

Если точки A₁, В₁, С₁ не лежат на прямой, то они являются вершинами треугольника. Поэтому A₁C₁ <A₁B₁  + B₁C₁. По определению движения отсюда следует, что АС<АВ+ВС. Однако по свойству измерения отрезков АС = АВ + ВС.

Мы пришли к противоречию. Значит, точка B₁ лежит на прямой А₁С₁. Первое утверждение теоремы доказано.

Покажем теперь, что точка B₁ лежит между A₁ и C₁. Допустим, что точка A₁ лежит между точками B₁ и C₁. Тогда A₁B₁ + А₁С₁ =B₁C₁ и,

следовательно, АВ + AС=ВС. Но это противоречит равенству AВ + ВС=АС. Таким образом, точка A₁ не может лежать между точками B₁ и C₁.

Аналогично доказывается, что точка C₁ не может лежать между точками A₁ и B₁.

Так как из трех точек A₁, В₁, С₁, одна лежит между двумя другими, то этой точкой может быть только B₁. Теорема доказана полностью.

Из теоремы 9.1 следует, что при движении прямые переходят в прямые, полупрямые — в полупрямые, отрезки — в отрезки (рис. 185).

Докажем, что при движении сохраняются углы между полупрямыми.
 
 

Пусть АВ и АС — две полупрямые, исходящие из точки А, не лежащие на одной прямой (рис. 186). При движении эти полупрямые переходят в некоторые полупрямые A₁, В₁, и А₁С₁. Так как движение сохраняет расстояния, то треугольники ABC и A₁, В₁, С₁, равны по третьему признаку равенства треугольников. Из равенства треугольников следует равенство углов ВАС и В₁А₁С₁, что и требовалось доказать.

А. В. Погорелов, Геометрия для 7-11 классов, Учебник для общеобразовательных учреждений

_{Математика для 8 класса, учебники и книги по математике скачать, библиотека онлайн}

Содержание урока
 конспект урока                       
 опорный каркас  
 презентация урока
 акселеративные методы 
 интерактивные технологии 

Практика
 задачи и упражнения 
 самопроверка
 практикумы, тренинги, кейсы, квесты
 домашние задания
 дискуссионные вопросы
 риторические вопросы от учеников
 
Иллюстрации
 аудио-, видеоклипы и мультимедиа 
 фотографии, картинки 
 графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты

Дополнения
 рефераты
 статьи 
 фишки для любознательных 
 шпаргалки 
 учебники основные и дополнительные
 словарь терминов                          
 прочие 

Совершенствование учебников и уроков
 исправление ошибок в учебнике
 обновление фрагмента в учебнике 
 элементы новаторства на уроке 
 замена устаревших знаний новыми 
 
Только для учителей
 идеальные уроки 
 календарный план на год  
 методические рекомендации  
 программы
 обсуждения


Интегрированные уроки

Если у вас есть исправления или предложения к данному уроку, напишите нам.

Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.