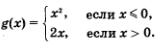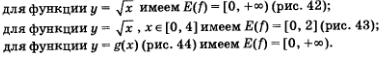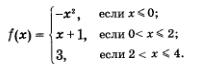|
Гипермаркет знаний>>Математика>>Математика 9 класс>>Математика: Определение числовой функции. Область определения, область значений функции
ОПРЕДЕЛЕНИЕ ЧИСЛОВОЙ ФУНКЦИИ. ОБЛАСТЬ ОПРЕДЕЛЕНИЯ, ОБЛАСТЬ ЗНАЧЕНИЙ ФУНКЦИИ
За два года изучения школьного курса алгебры вы уже привыкли к тому, что термин «функция» используется практически постоянно. Это и понятно: ведь математика изучает математические модели, а описание большинства этих моделей на математическом языке так или иначе связано с функциями. Но в математике действует закон: если используется какой-то термин, то его надо точно определить. За два года изучения курса алгебры мы с вами накопили достаточно много примеров, подтверждающих этот закон. Так, в 7-м классе мы ввели термин «степень с натуральным показателем», точно его определив: «под a2, где n = 2, 3, 4, ... , понимается произведение n множителей, каждый из которых равен о; под а1 понимается само число а». В 8-м классе мы ввели термин «квадратный корень из неотрицательного числа», дав ему точное определение: 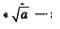 это такое неотрицательное число, квадрат которого равен a». И так далее и тому подобное — вы сами можете привести аналогичные примеры. это такое неотрицательное число, квадрат которого равен a». И так далее и тому подобное — вы сами можете привести аналогичные примеры.
В то же время были случаи, когда мы вводили термин и начинали им пользоваться, но точного определения не формулировали, ограничиваясь приблизительным истолкованием термина. Так было, в частности, с термином «функция». Почему же мы в 7-м классе, как только стали использовать понятие функции, не сформулировали точное определение, почему не сделали этого и в 8-м классе?
Дело в том, что история развития математики показывает: были понятия, которые человечество активно и длительное время использовало как рабочий инструмент, не задумываясь о том, как его определить. Лишь накопив необходимый опыт в работе с тем или иным понятием, математики начинали думать о его формальном определении. Разумеется, не всегда первые попытки определить то или иное понятие, вроде бы ясное на интуитивном уровне, оказывались удачными, их приходилось впоследствии дополнять, уточнять. Так было и с понятием функции.
Проанализируем наш опыт работы с термином «функция». В 7-м классе мы ввели термин «линейная функция», понимая под этим уравнение с двумя переменными специального вида у = кх + m и рассматривая переменные хи у как неравноправные: х — независимая переменная, у — зависимая переменная. Затем задались вопросом: а не встречаются ли при описании реальных процессов математические модели подобного вида, но такие, у которых у выражается через х не по формуле у = кх + m, а по какой-либо иной формуле? Ответ на этот вопрос был получен сразу: встречаются. В 7-м классе, кроме упомянутой линейной функции, мы изучили математическую модель у = х2, в 8-м классе добавили к ним модели 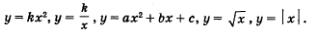
Постепенно мы начали осознавать, что, изучая какой-либо реальный процесс, обычно обращают внимание на две переменные величины, участвующие в нем (в более сложных процессах участвуют более двух величин, но мы такие процессы пока не рассматривали). Одна из них меняется как бы сама по себе, независимо ни от чего (такую переменную чаще всего обозначают буквой x), а другая переменная принимает значения, каждое из которых каким-то образом зависит от выбранного значения переменной х (такую зависимую переменную чаще всего обозначают буквой у). Математической моделью реального процесса как раз и является запись на математическом языке зависимости у от х: у = fх). Такие математические модели мы называли функциями.
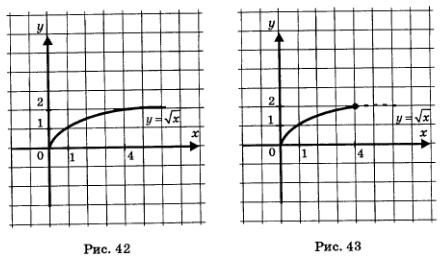
Математическая модель у = f(х) обычно дополняется указанием на то, из какого числового множества берутся значения независимой переменной х. Например, мы говорили о функции 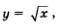 , подразумевая, что , подразумевая, что 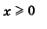 (график функции изображен на рис. 42), но мы рассматривали и функцию (график функции изображен на рис. 42), но мы рассматривали и функцию 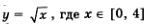 (график функции изображен на рис. 43). Это разные математические модели, значит, и разные функции. (график функции изображен на рис. 43). Это разные математические модели, значит, и разные функции.
Использование математической модели вида у = f(x) оказывается удобным во многих случаях, в частности тогда, когда реальный процесс описывается различными формулами на разных промежутках изменения независимой переменной. Вот одна из таких функций: у = g {х), где 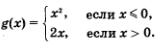
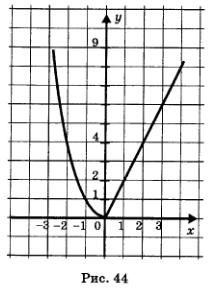
График функции изображен на рис. 44. Помните, как строить такие графики? Сначала надо построить параболу у = х2 и взять ее часть при 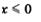 (левая ветвь параболы), затем построить прямую у = 2х и взять ее часть при х > 0. И, наконец, надо обе выделенные части объединить на одном рисунке, т.е. построить в одной координатной плоскости. Этот пример (или аналогичные) мы рассматривали и в 7-м, и в 8-м классах. (левая ветвь параболы), затем построить прямую у = 2х и взять ее часть при х > 0. И, наконец, надо обе выделенные части объединить на одном рисунке, т.е. построить в одной координатной плоскости. Этот пример (или аналогичные) мы рассматривали и в 7-м, и в 8-м классах.
Так что же такое функция? Проведенный выше анализ и наш опыт изучения конкретных функций в 7-м и 8-м классах позволяют выделить два существенных момента.
1. Запись у = f(х) представляет собой п р а в ил о (обычно говорят «правило f»), с помощью которого, зная конкретное значение независимой переменной х, можно найти соответствующее значение переменной у.
2. Указывается числовое множество X (чаще всего какой-то числовой промежуток), откуда берутся значения независимой переменной х.
Теперь мы можем сформулировать одно из главных определений школьного курса алгебры (да, пожалуй, и всей математики).
Определение 1. Если даны числовое множество X и правило f, позволяющее поставить в соответствие каждому элементу х из множества X определенное число у, то говорят, что задана функция у = f(х) с областью определения X; пишут у = f(x), х є X. При этом переменную х называют независимой переменной или аргументом, а переменную у — зависимой переменной.
Замечание. В реальной жизни мы часто говорим: «каковы мои функции» или «каковы мои функциональные обязанности», — спрашивая тем самым соответственно: «каков круг моих действий, моих обязанностей» или «что я должен делать, как действовать». Фактически в реальной жизни слово «функция» означает «действие» или «правила действий». Обратите внимание, что фактически тот же смысл имеет и математический термин «функция», который мы разъяснили выше в определении 1.
Если f(х) — алгебраическое выражение и множество X совпадает с областью определения этого выражения, то действует соглашение: вместо записи у = f(x), х є X, используется более короткая запись: у = f(х), хотя, подчеркнем, такая запись не совсем соответствует определению 1. Но математики стараются быть экономными во всем: и в употреблении слов в формулировках, и в записях математических утверждений.
Для области определения функции у = f(х), х є X, иногда удобно использовать обозначение D(f). Например:

Еще раз подчеркнем, что нельзя говорить о функции у = f(x) без указания ее области определения, которая или указывается явно, или подразумевается — в случае, если область определения функции у = f(x) совпадает с областью определения выражения f(x) (такую область определения иногда называют естественной).
Пример 1. Найти область определения функции:
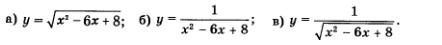
Р е ш е н и е. а) Так как область определения функции явно не указана, подразумевается, что она совпадает с областью определения выражения 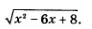 Таким образом, речь идет о поиске естественной области определения функции. Под знаком квадратного корня может находиться только неотрицательное число, значит, задача сводится к решению квадратного неравенства Таким образом, речь идет о поиске естественной области определения функции. Под знаком квадратного корня может находиться только неотрицательное число, значит, задача сводится к решению квадратного неравенства 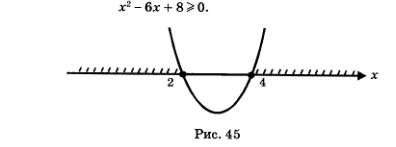
Найдя корни квадратного трехчлена 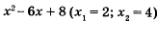 и схематически построив параболу у = х2 - 6х + 8 (рис. 45), выбираем интересующие нас промежутки: и схематически построив параболу у = х2 - 6х + 8 (рис. 45), выбираем интересующие нас промежутки: 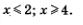
Обратите внимание, что точки 2 и 4 отмечены закрашенными кружочками; их следует включить в ответ, поскольку заданное неравенство — нестрогое.
Итак, 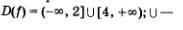 знак объединения множеств. знак объединения множеств.
б) Функция 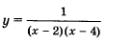 определена в любой точке х, за исключением точек 2 и 4 — при этих значениях х знаменатель дроби обращается в 0. Ответ можно записать так: определена в любой точке х, за исключением точек 2 и 4 — при этих значениях х знаменатель дроби обращается в 0. Ответ можно записать так:
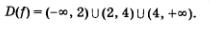
Впрочем, на практике можно использовать сокращенную запись: 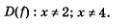
в) Здесь задача сводится к решению неравенства х2 - 6х + 8 > 0.
Воспользовавшись геометрической моделью, представленной на рис. 45, но исключив из рассмотрения точки х — 2 и х = 4, получим 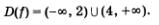
Определение 2. Множество всех значений функции у = f(x), х є X, называют областью значений функции и обозначают Е(f).
Если известен график функции, то область значений функции найти сравнительно нетрудно. Для этого достаточно спроецировать график на ось ординат. То числовое множество, геометрическая модель которого получится на оси ординат в результате указанного проецирования, и будет представлять собой Е(f)- Например:
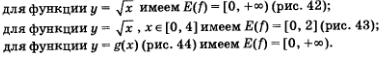
Завершая этот параграф, рассмотрим пример, который в определенном смысле является итогом сказанного.
Пример 2. Дана функция у = f(x), где 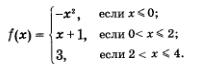
а) Найти D (f);
б) вычислить f (-2), f (0), f (2), f (3,2), f (4), f (5);
в) найти Е (f).
Р е ш е н и е. а) Область определения функции состоит из трех промежутков: (-оо, 0], (0, 2] и (2, 4]. Объединяя их, получаем луч (-оо, 4].
Итак, D(f) = (-оо, 4].
б) Значение х = - 2 удовлетворяет условию 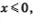 следовательно, f (-2) надо вычислять по первой строке задания функции. Имеем f(х) = -х2, значит, f (-2) = -(-2)2 = - 4. следовательно, f (-2) надо вычислять по первой строке задания функции. Имеем f(х) = -х2, значит, f (-2) = -(-2)2 = - 4.
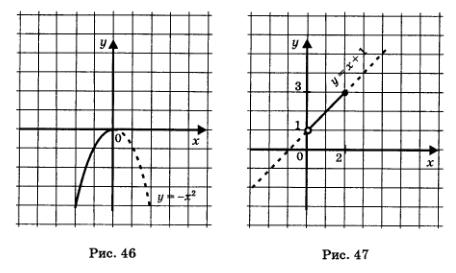
Значение х = 0 удовлетворяет условию 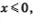 следовательно, f (0) надо вычислять по первой строке задания функции. Имеем f (х) = -х2, значит, f(0) = -О2 = 0. следовательно, f (0) надо вычислять по первой строке задания функции. Имеем f (х) = -х2, значит, f(0) = -О2 = 0.
Значение х — 2 удовлетворяет условию 0 < х < 2, следовательно, /(2) надо вычислять по второй строке задания функции. Имеем /(х) = х + 1, значит, /(2) = 2+1 = 3.
Значение х = 3,2 удовлетворяет условию 2 < х < 4, следовательно, /(3,2) надо вычислять по третьей строке задания функции. Имеем /(х) = 3, значит, /(3,2) = 3.
Значение х = 4 удовлетворяет условию 2 < х < 4, следовательно, /(4) надо вычислять по третьей строке задания функции. Имеем /(х) = 3, значит, /(4) = 3.
Значение х = 5 не удовлетворяет ни одному из трех условий задания функции, а потому /(5) в данном случае вычислить нельзя, точка х = 5 не принадлежит области определения функции. Задание вычислить /(5) в данном случае некорректно.
в) Область значений функции, как мы уже отметили выше, удобнее всего находить с помощью графика функции. Построение графика осуществим «по кусочкам». Сначала построим параболу у = -х2 и выделим ее часть на луче (-оо, 0] (рис. 46). Затем построим прямую у = х + 1 и выделим ее часть на полуинтервале (0, 2] (рис. 47). Далее построим прямую у — 3 и выделим ее часть на полуинтервале (2, 4] (рис. 48). Наконец, все три «кусочка» изобразим в одной системе координат — это и будет график функции у = /(х) (рис. 49).
70
3.12. ||
ЧИСЛОВЫЕ ФУНКЦИИ
У А к
3
X
0 2 4
У А к
3 /
1/
1 X
/ 0 2 4
/
/
Рис. 48
Рис. 49
Теперь хорошо видно, что область значений функции состоит из двух промежутков: луча (-оо, 0] — он сплошь заполняется ординатами точек ветви параболы у = -х2, х < 0 — и полуинтервала (1, 3] — он сплошь заполняется ординатами точек участка прямой у = х+ 1,0<х<2. Итак, Е(/) = (-оо, 0]II(1, 3]. О
А.Г. Мордкович Алгебра 9 класс
Материалы по математике онлайн, задачи и ответы по классам, планы конспектов уроков по математике скачать
Содержание урока
 конспект урока конспект урока
 опорный каркас опорный каркас
 презентация урока презентация урока
 акселеративные методы акселеративные методы
 интерактивные технологии
Практика интерактивные технологии
Практика
 задачи и упражнения задачи и упражнения
 самопроверка самопроверка
 практикумы, тренинги, кейсы, квесты практикумы, тренинги, кейсы, квесты
 домашние задания домашние задания
 дискуссионные вопросы дискуссионные вопросы
 риторические вопросы от учеников
Иллюстрации риторические вопросы от учеников
Иллюстрации
 аудио-, видеоклипы и мультимедиа аудио-, видеоклипы и мультимедиа
 фотографии, картинки фотографии, картинки
 графики, таблицы, схемы графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты
Дополнения притчи, поговорки, кроссворды, цитаты
Дополнения
 рефераты рефераты
 статьи статьи
 фишки для любознательных фишки для любознательных
 шпаргалки шпаргалки
 учебники основные и дополнительные учебники основные и дополнительные
 словарь терминов словарь терминов
 прочие
Совершенствование учебников и уроков прочие
Совершенствование учебников и уроков
 исправление ошибок в учебнике исправление ошибок в учебнике
 обновление фрагмента в учебнике обновление фрагмента в учебнике
 элементы новаторства на уроке элементы новаторства на уроке
 замена устаревших знаний новыми
Только для учителей замена устаревших знаний новыми
Только для учителей
 идеальные уроки идеальные уроки
 календарный план на год календарный план на год
 методические рекомендации методические рекомендации
 программы программы
 обсуждения
Интегрированные уроки обсуждения
Интегрированные уроки
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.
|