Гипермаркет знаний>>Математика>>Математика 9 класс>>Математика: Признак подобия треугольников по двум сторонам и углу между ними

                                    ПРИЗНАК ПОДОБИЯ ТРЕУГОЛЬНИКОВ ПО ДВУМ СТОРОНАМ И УГЛУ МЕЖДУ НИМИ

Теорема 11.3. Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, образованные этими сторонами, равны, то треугольники подобны.

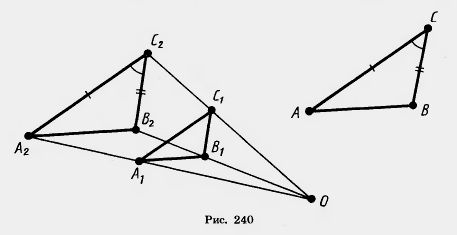
Доказательство (аналогично доказательству теоремы 11.2). Пусть у треугольников ABC и A₁B₁C₁ C=C₁ и AC = kA₁C₁, BC = kB₁C₁. Докажем, что

АВС A₁B₁C₁,.

Подвергнем треугольник A₁B₁C₁ преобразованию подобия с коэффициентом подобия к, например гомотетии (рис. 240).

При этом получим некоторый треугольник A₂B₂C₂, равный треугольнику ABC. Действительно, так как преобразование подобия сохраняет углы, то

C₂= C₁. А значит, у треугольников ABC и A₂B₂C₂, C=C₂. Далее, A₂C₂ = kA₁C₁=AC, B₂C₂ = kB₁C₁=BC. Следовательно, треугольники ABC и A₂B₂C₂ равны по первому признаку (по двум сторонам и углу между ними).

Так как треугольники A₁B₁C₁ и A₂B₂C₂ гомотетичны и, значит, подобны, а треугольники A₂B₂C₂ и ABC равны и поэтому тоже подобны, то треугольники A₁B₁C₁ и ABC подобны. Теорема доказана.

 
Задача (31). В треугольнике ABC с острым углом С проведены высоты АЕ и BD (рис. 241). Докажите, что АВСEDC.

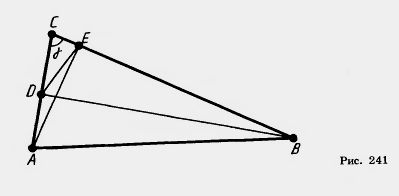
Решение. У треугольников ABC и EDC угол при вершине С общий. Докажем пропорщюнальность сторон треугольников, прилежащих к этому углу.

Имеем ЕС = =АС cosy, DC=ВС cosy. То есть стороны, прилежащие к углу С, у треугольников пропорциональны. Значит, АВСEDC. По двум сторонам и углу между ними.

А. В. Погорелов, Геометрия для 7-11 классов, Учебник для общеобразовательных учреждений

_{Математика за 9 класс бесплатно скачать, планы конспектов уроков, готовимся к школе онлайн}

Содержание урока
 конспект урока                       
 опорный каркас  
 презентация урока
 акселеративные методы 
 интерактивные технологии 

Практика
 задачи и упражнения 
 самопроверка
 практикумы, тренинги, кейсы, квесты
 домашние задания
 дискуссионные вопросы
 риторические вопросы от учеников
 
Иллюстрации
 аудио-, видеоклипы и мультимедиа 
 фотографии, картинки 
 графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты

Дополнения
 рефераты
 статьи 
 фишки для любознательных 
 шпаргалки 
 учебники основные и дополнительные
 словарь терминов                          
 прочие 

Совершенствование учебников и уроков
 исправление ошибок в учебнике
 обновление фрагмента в учебнике 
 элементы новаторства на уроке 
 замена устаревших знаний новыми 
 
Только для учителей
 идеальные уроки 
 календарный план на год  
 методические рекомендации  
 программы
 обсуждения


Интегрированные уроки

Если у вас есть исправления или предложения к данному уроку, напишите нам.

Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.