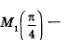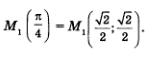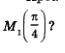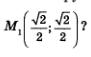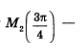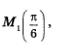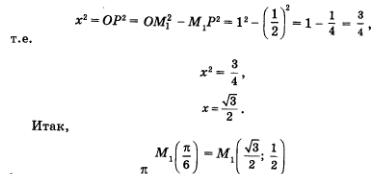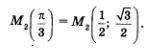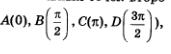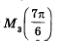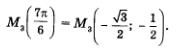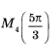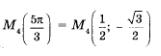|
Гипермаркет знаний>>Математика>>Математика 9 класс>>Математика: Числовая окружность на координатной плоскости
ЧИСЛОВАЯ ОКРУЖНОСТЬ НА КООРДИНАТНОЙ ПЛОСКОСТИ
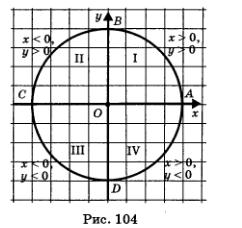
Расположим числовую окружность в декартовой прямоугольной системе координат хОу так, как показано на рис. 104: центр окружности совмещен с началом координат, радиус окружности принимается за масштабный отрезок. Начальная точка А числовой окружности совмещена с точкой (1; 0) на оси х. При этом 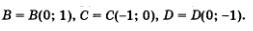 Каждая точка числовой окружности имеет в системе хОу свои координаты, причем: у точек первой четверти — х > 0, у> 0; у точек второй четверти — х < 0, у > 0; у точек третьей четверти — х < 0, у < 0; у точек четвертой четверти — х > 0, у < 0 (рис. 104). Каждая точка числовой окружности имеет в системе хОу свои координаты, причем: у точек первой четверти — х > 0, у> 0; у точек второй четверти — х < 0, у > 0; у точек третьей четверти — х < 0, у < 0; у точек четвертой четверти — х > 0, у < 0 (рис. 104).
Для любой точки М(х; у) числовой окружности выполняются неравенства: 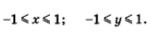
Нетрудно составить уравнение числовой окружности. Для этого заметим, во-первых, что центром окружности служит начало координат, а уравнение окружности с центром в начале координат и радиусом R имеет вид х2 + у2 = R2. Заметим, во-вторых, что R— 1; значит, уравнение числовой окружности имеет вид х2+у2 = 1.
Нам важно научиться отыскивать координаты точек числовой окружности, прежде всего тех, которые представлены на первом и втором макетах (рис. 100 и 101). Начнем с точек первого макета:
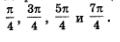
Точка 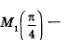 середина первой четверти. Опустим из точки М. перпендикуляр М2Р на прямую ОА и рассмотрим треугольник ОМ}Р (рис. 105). Так как дуга АМХ составляет половину дуги АВ, то середина первой четверти. Опустим из точки М. перпендикуляр М2Р на прямую ОА и рассмотрим треугольник ОМ}Р (рис. 105). Так как дуга АМХ составляет половину дуги АВ, то 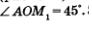 Значит, ОМ1Р — равнобедренный прямоугольный треугольник; его катеты ОР и М1Р равны, т.е. у точки Мх абсцисса и ордината равны: х = у. Кроме того, координаты точки М1х; у) удовлетворяют уравнению окружности х2 + у2 = 1. Таким образом, для отыскания координат точки Мх нужно решить систему уравнений Значит, ОМ1Р — равнобедренный прямоугольный треугольник; его катеты ОР и М1Р равны, т.е. у точки Мх абсцисса и ордината равны: х = у. Кроме того, координаты точки М1х; у) удовлетворяют уравнению окружности х2 + у2 = 1. Таким образом, для отыскания координат точки Мх нужно решить систему уравнений
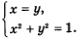
Подставив х вместо у во второе уравнение системы, получим:
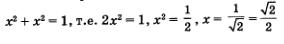
1 1 -ЛИ
(мы учли, что абсцисса точки М1 положительна). А так как у = х,то И 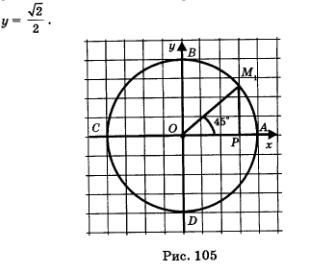
Итак,
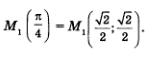
Проанализируем полученное равенство. Что означает запись 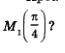 Она означает, что точка М1 числовой окружности соответствует числу Она означает, что точка М1 числовой окружности соответствует числу 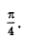 А что означает запись А что означает запись 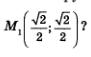 Она означает, Она означает,
что точка имеет соответствующие координаты в прямоугольной системе координат хОу. И в дальнейшем будем придерживаться подобного способа записи: если будет написано М(1), то это значит, что точка М числовой окружности соответствует числу Ц если будет написано М(х; у), то это значит, что числа хиу являются соответственно абсциссой и ординатой точки М. Таким образом, (х; у) — декартовы координаты точки М, а I — «криволинейная» координата точки М на числовой окружности.
Рассмотрим точку 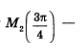 середину второй четверти. Рассуждая, как и выше, получим для модуля абсциссы и для модуля ординаты этой точки те же значения середину второй четверти. Рассуждая, как и выше, получим для модуля абсциссы и для модуля ординаты этой точки те же значения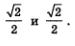 Но, учтя, что во второй четверти х < 0, а у > О, делаем вывод: Но, учтя, что во второй четверти х < 0, а у > О, делаем вывод:

Теперь найдем координаты точек, изображенных на втором макете (рис. 101). Возьмем точку 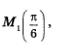 опустим из нее перпендикуляр М1Р на прямую ОА и рассмотрим прямоугольный треугольник ОМхР (рис. 106). Гипотенузой этого треугольника является ОМ , причем ОМх = 1. Угол МуОР равен 30°, поскольку дуга АМ1 составляет треть дуги АВ, а дуга АВ содержит 90°. Из геометрии известно, что катет прямоугольного треугольника, лежащий против угла 30°, равен половине гипотенузы. Значит, опустим из нее перпендикуляр М1Р на прямую ОА и рассмотрим прямоугольный треугольник ОМхР (рис. 106). Гипотенузой этого треугольника является ОМ , причем ОМх = 1. Угол МуОР равен 30°, поскольку дуга АМ1 составляет треть дуги АВ, а дуга АВ содержит 90°. Из геометрии известно, что катет прямоугольного треугольника, лежащий против угла 30°, равен половине гипотенузы. Значит, 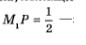 это ордината точки М: это ордината точки М:
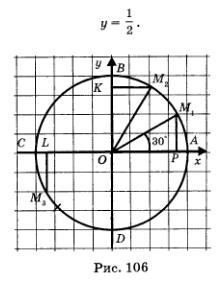
По теореме Пифагора,
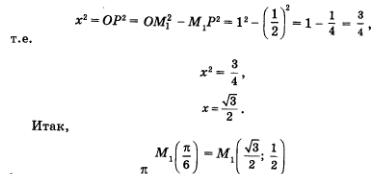
(мы учли, что точка 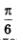 принадлежит первой четверти, а потому обе ее координаты — положительные числа). принадлежит первой четверти, а потому обе ее координаты — положительные числа).
С точкой 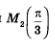 связан тот же прямоугольный треугольник, только ориентированный по-другому (рис. 106). Получаем связан тот же прямоугольный треугольник, только ориентированный по-другому (рис. 106). Получаем 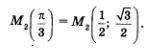
Те же самые значения (с точностью до знака) будут координатами всех остальных точек второго макета (исключая, разумеется, точки 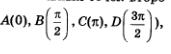 причем по чертежу нетрудно определить, какая координата равна по модулю числу причем по чертежу нетрудно определить, какая координата равна по модулю числу 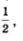 а какая —числу а какая —числу 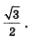 Возьмем для примера точку Возьмем для примера точку 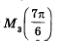 (рис. 106). Будем рассуждать так. Проведем перпендикуляр М2L к оси х. Во-первых, (рис. 106). Будем рассуждать так. Проведем перпендикуляр М2L к оси х. Во-первых, 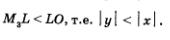
Значит, из двух чисел 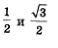 в качестве ординаты точки М3 нужно взять меньшее. Окончательно получаем в качестве ординаты точки М3 нужно взять меньшее. Окончательно получаем
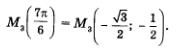
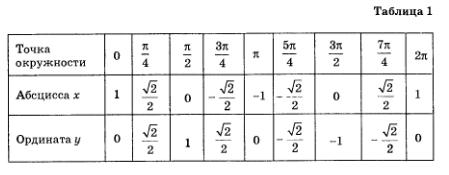
А теперь возьмите точку 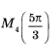 и попробуйте, проведя аналогичные рассуждения, наити декартовы координаты точки. Мы же пока приведем итоговую таблицу, с помощью которой вы сможете и попробуйте, проведя аналогичные рассуждения, наити декартовы координаты точки. Мы же пока приведем итоговую таблицу, с помощью которой вы сможете
проверить правильность своего вывода.
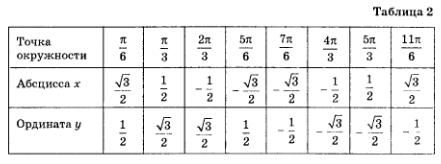
А теперь проверьте себя: 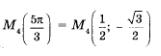 (см. предпоследнюю колонку таблицы 2). (см. предпоследнюю колонку таблицы 2).
Пример 1. Найти координаты точек числовой окружности:
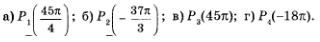
Решение. Во всех четырех случаях воспользуемся утверждением, полученным в предыдущем параграфе: числам t и 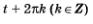 соответствует одна и та же точка числовой окружности. соответствует одна и та же точка числовой окружности.
а) Имеем
45я 45 5 5л 5я
—— = — • 71 = (10+ 7)71=1071+ -Г = -- + 2я-5. 4 4 4' 4 4
45я
Следовательно, числу соответствует та же точка числовой 5я
окружности, что и числу — (см. первый макет, рис. 100). Для точ-
5л ки — имеем х = - — 4 2 >У = 42 2 ' Значит,
Л ' 45яч / - 2
10* 161
5.18.
ЭЛЕМЕНТЫ ТЕОРИИ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ
б) Имеем
37я 37
•71 = -
12 +
71 =-1271- ~ = +271-(-6).
о 3
37я
Следовательно, числу —— соответствует та же точка число-
о
я Я
вой окружности, что и числу - - . А числу - - соответствует на чис-
о о
5я
ловои окружности та же точка, что и числу — (см. второй макет —
5я 1 73
рис. 101). Для точки — имеем х = - , г/ = - — . Таким образом,
о I 2
37я4 _ п ( 1 _
2 2' 2 /
в) 4571 = 4471+ 71 = 71 + 2т1-22. Значит, числу 45я соответствует та же точка числовой окружности, что и числу к, — это точка С(-1; 0). Итак,
Р3(4571) = Р3(-1;0).
г) —1871 = 0 + 271- (-9). Следовательно, числу —1871 соответствует та же точка числовой окружности, что и числу 0, — это точка А(1; 0). Итак,
Р4(-18т1) = Р4(1;0). <1
Пример 2. Найти на числовой окружности точки с ордина-1
той у = — и записать, каким числам I они соответствуют.
Решение. Прямая у = - пересекает числовую окружность
я
в двух точках: М и Р (рис. 107). Точка М соответствует числу -(см. второй макет — рис. 101), а значит, и любому числу вида
5я
^ + 2пк; точка Р соответствует числу — , а значит, и любому числу
5я
вида — + 2пк. Получили, как обычно говорят в таких случаях, две
я 5я
серии значений: — + 2пк и — + 2т1к.
о о
Ответ: 1= - + 271 к; I = о
5я
+ 2тгк.
162
5.18.
ЭЛЕМЕНТЫ ТЕОРИИ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ
= Л У л кВ
/
м. г
/
С
0 1 х
V
л
ч]
и
Рис. 107
Рис. 108
Пример 3. Найти на числовой окружности точки с абсцис-
72
СОИ X =
и записать, каким числам I они соответствуют.
42
Решение. Прямая х = —— пересекает числовую окружность
Зя
в двух точках: М и Р (рис. 108). Точка М соответствует числу —
(см. первый макет — рис. 100), а значит, и любому числу вида Зя 5я
— + 2пк; точка Р соответствует числу — , а значит, и любому
5я
числу вида у + 2пк.
Зя 5я
Ответ: 1= — + 2пк; I = — + 2пк. 4 4
Замечание. Решая пример 3, можно было рассуждать немного по-другому: точка Р соответствует чис-
Зя . Зя
лу--, а значит, и любому числу вида--+ 2пк.
4 4
Зя
Получили две серии значений: / =--\-2пк (для точ-
Зя 4
ки М)и/ = -— + 2пк (для точки Р). Чем это лучше по
сравнению с записью ответа к примеру 3? Тем, что обе
серии значений можно охватить одной записью:
Зя „ , /= ± — +2пк. 4
11*
163
5.17.||
ЭЛЕМЕНТЫ ТЕОРИИ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ
А.Г. Мордкович Алгебра 9 класс
Материалы по математике онлайн, задачи и ответы по классам, планы конспектов уроков по математике скачать
Содержание урока
 конспект урока конспект урока
 опорный каркас опорный каркас
 презентация урока презентация урока
 акселеративные методы акселеративные методы
 интерактивные технологии
Практика интерактивные технологии
Практика
 задачи и упражнения задачи и упражнения
 самопроверка самопроверка
 практикумы, тренинги, кейсы, квесты практикумы, тренинги, кейсы, квесты
 домашние задания домашние задания
 дискуссионные вопросы дискуссионные вопросы
 риторические вопросы от учеников
Иллюстрации риторические вопросы от учеников
Иллюстрации
 аудио-, видеоклипы и мультимедиа аудио-, видеоклипы и мультимедиа
 фотографии, картинки фотографии, картинки
 графики, таблицы, схемы графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты
Дополнения притчи, поговорки, кроссворды, цитаты
Дополнения
 рефераты рефераты
 статьи статьи
 фишки для любознательных фишки для любознательных
 шпаргалки шпаргалки
 учебники основные и дополнительные учебники основные и дополнительные
 словарь терминов словарь терминов
 прочие
Совершенствование учебников и уроков прочие
Совершенствование учебников и уроков
 исправление ошибок в учебнике исправление ошибок в учебнике
 обновление фрагмента в учебнике обновление фрагмента в учебнике
 элементы новаторства на уроке элементы новаторства на уроке
 замена устаревших знаний новыми
Только для учителей замена устаревших знаний новыми
Только для учителей
 идеальные уроки идеальные уроки
 календарный план на год календарный план на год
 методические рекомендации методические рекомендации
 программы программы
 обсуждения
Интегрированные уроки обсуждения
Интегрированные уроки
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.
|