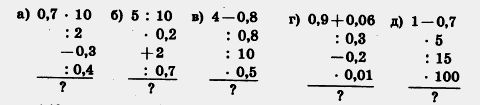Гипермаркет знаний>>Математика>>Математика 6 класс>>Математика:Наибольший общий делитель. Взаимно простые числа

                                    6. Наибольший общий делитель. Взаимно простые числа

Задача. Какое наибольшее число одинаковых подарков можно составить из 48 конфет «Ласточка» и 36 конфет «Чебурашка», если надо использовать все конфеты?

Решение. Каждое из чисел 48 и 36 должно делиться на число подарков. Поэтому сначала выпишем все делители числа 48.

Получим: 2, 3, 4, 6, 8, 12, 16, 24, 48.

Затем выпишем все делители числа 36.

Получим: 1, 2, 3, 4, 6, 9, 12, 18, 36.

Общими делителями чисел 48 и 36 будут: 1, 2, 3, 4, 6, 12.

Видим, что наибольшим из этих чисел является 12. Его называют наибольший общим делителем чисел 48 и 36.

Значит, можно составить 12 подарков. В каждом подарке будет 4 конфеты «Ласточка» (48:12=4) и 3 конфеты «Чебурашка» (36:12=3).

Наибольшее натуральное число, на которое делятся без остатка числа а и b, называют наибольшим общим делителем этих чисел.

Найдем наибольший общий делитель чисел 24 и 36.

Делителями 24 будут 1, 2, 3, 4, 6, 8, 12, 24, а делителями 35 будут 1, б, 7, 35.

Видим, что числа 24 и 35 имеют только один общий делитель — число 1. Такие числа называют взаимно простыми.

Натуральные числа называют взаимно простыми, если их наибольший общий делитель равен 1.

Наибольший общий делитель можно найти, не выписывая всех делителей данных чисел.

Разложим на множители числа 48 и 36, получим: 48 = 2 • 2 • 2 • 2 • 3, 36 = 2 • 2 • 3 • 3.

Из множителей, входящих в разложение первого из этих чисел, вычеркнем те, которые не входят в разложение второго числа (т. е. две двойки).

Остаются множители 2 • 2 • 3. Их произведение равно 12. Это число и является наибольшим общим делителем чисел 48 и 36.

Так же находят наибольший общий делитель трех и более. чисел.

Чтобы найти наибольший общий делитель нескольких натуральных чисел, надо: 1) разложить их на простые множители; 2) из множителей, входящих в разложение одного из этих чисел, вычеркнуть те, которые не входят в разложение других чисел; 3) найти произведение оставшихся множителей.

Если все данные числа делятся на одно из них, то это число и является наибольшим общим делителем данных чисел.

Например, наибольшим общим делителем чисел 16, 45, 75 и 180 будет число 15, так как на него делятся все остальные числа: 45, 75 и 180.

 ? Какое число называют наибольшим общим делителем двух натуральных чисел? Какие два числа называют взаимно простыми? Как найти наибольший общий делитель нескольких натуральных чисел? Число а кратно числу b. Какое число является наибольшим общим делителем чисел а и b?

 К  139. Найдите все общие делители чисел: а) 18 и 60; б) 72, 96 и 120; в) 35 и 88.

140. Найдите разложение на простые множители наибольшего общего делителя чисел а и b, если: а) а = 2 • 2 • 3 • 3 и b = 2 • 3 • 3 • 5; б) а = 5 • 5 • 7 • 7 • 7 и b = 3 • 5 • 7 • 7.

141.    Найдите наибольший общий делитель чисел:

а)    12 и 18;              в) 675 и 825;              д) 324, 111 и 432;
б)    50 и 175;             г) 7920 и 594;            е) 320, 640 и 960.

142.    Являются ли взаимно простыми числа:

а) 35 и 40; б) 77 и 20; в) 10, 30, 41; г) 231 и 280?

143.    Найдите среди чисел 9, 14, 15 и 27 три пары взаимно простых чисел.

144.    Запишите все правильные дроби со знаменателем 12, у которых числитель и знаменатель — взаимно простые числа.

145.    Ребята получили на новогодней елке одинаковые подарки. Во всех подарках вместе было 123 апельсина и 82 яблока. Сколько ребят присутствовало на елке? Сколько апельсинов и сколько яблок было в каждом подарке?

146. Для поездки за город работникам завода было выделено несколько автобусов, с одинаковым числом мест в каждом автобусе. 424 человека поехали в лес, а 477 человек — на озеро. Все места в автобусах были заняты, и ни одного человека не осталось без места. Сколько автобусов было выделено и сколько пассажиров было в каждом автобусе?

П 147. Вычислите устно:

148. С помощью рисунка 7 определите, являются ли числа a, b и с простыми.

149.    Существует ли куб, ребро которого выражается натуральным числом и у которого:

а)    сумма длин всех'ребер выражается простым числом;
б)    площадь поверхности выражается простым числом?

150.    Разложите на простые множители числа:

а) 875; 2376; 5625; б) 2025; 3969; 13125.

151.    Почему, если одно число можно разложить на два простых множителя, а второе — на три простых множителя, то эти числа не равны?

152.    Можно ли найти четыре различных простых числа, чтобы произведение двух из них равнялось произведению двух других?

153.    Найдите значение выражения:

а)    (3 • 8 • 5-11):(8 • 11); в) (2 • 3 • 7 •1 •3):(3 •7);
б)    (2 •2 •3 •5 •7):(2 •3 •7); г) (3 •5 • 11 • 17 • 23):(3 • 11 •17).

154.    Сравните:

155. С помощью транспортира постройте АОВ=35° и DEF = 140°.

156.    Решите задачу:

1)    Луч ОМ разделил развернутый- угол АОВ на два угла АОМ и MOB. Угол АОМ в 3 раза больше угла MOB. Чему равны углы АОМ и ВОМ. Постройте эти углы.
2)    Луч ОК разделил развернутый угол COD на два угла СОК и KOD. Угол СОК в 4 раза меньше угла KOD. Чему равны углы СОК и KOD? Постройте эти углы.

157.    Решите задачу:

1) Рабочие отремонтировали дорогу длиной 820 м за три дня. Во вторник они отремонтировали этой дороги, а в среду оставшейся части. Сколько метров дороги отремонтировали рабочие в четверг?

2) На ферме содержатся коровы, овцы и козы, всего 3400 животных. Овцы и козы вместе составляют всех животных, а козы составляют общего числа овец и коз. Сколько на ферме коров, сколько овец и сколько коз?

158.    Представьте в виде обыкновенной дроби числа 0,3; 0,13; 0,2 и в виде десятичной дроби числа —

159.    Выполните действие, записав каждое число в виде десятичной дроби:

а)

М 160. Вы умеете представлять числа в виде произведения простых чисел. Попробуйте представить в виде суммы простых слагаемых числа 10, 36', 54, 15, 27 и 49 так, чтобы слагаемых было возможно меньше. Какие предложения о представлении чисел в виде суммы простых слагаемых вы можете высказать?

Д  161. Найдите наибольший общий делитель чисел а и b, если:

а)    а = 3 • 3 • 5 • 5 • 5 • 7, 6 = 3 • 5 • 5 • 11;
б)    а = 2 • 2 • 2 • 3 • 5 • 7, 6 = 3 • 11 • 13.

162.    Найдите наибольший общий делитель чисел:

а) 585 и 360; б) 680 и 612; в) 60, 80 и 48; г) 195, 156 и 260.

163.    Докажите, что числа 864 и 875 взаимно простые.

164.    Сравните:

165.    Постройте угол А ОС, равный 130°. Проведите внутри угла АОС луч ОВ так, чтобы /LBOC=40°. Измерьте угол АОВ.
166.    В городе построен завод, на котором будут работать 840 рабочих следующих профессий: токари, слесари и фрезеровщики. При этом токарей будет втрое, а слесарей вдвое больше, чем фрезеровщиков. Сколько токарей нужно для завода?
23    
167.    В инкубатор заложили 1200 яиц. Из — всех яиц вылу-
24    
пились цыплята. При этом оказалось, что петушки составляют
-f- всех вылупившихся цыплят. Сколько петушков и сколько
о
курочек вылупилось из яиц?
166. Представьте в виде обыкновенной дроби: 0,5; 0,16; 0,25.
160. Представьте в виде десятичной дроби:
5 * 125 ' 20 * 2 ' 170. Найдите значение выражения:
а)    1,53 * 54—0,42 • (512—491,2) +1,116;
б)    ((27,12 + 43,08) • 0,007 - 0,0314) • 100.

Н.Я.Виленкин, А.С. Чесноков, С.И. Шварцбурд, В.И.Жохов, Математика для 6 класса, Учебник для средней школы

_{Материалы по математике за 6 класс скачать, конспект по математике , учебники и книги скатать бесплатно, школьная программа онлайн}

Содержание урока
 конспект урока
 опорный каркас  
 презентация урока
 акселеративные методы 
 интерактивные технологии 

Практика
 задачи и упражнения 
 самопроверка
 практикумы, тренинги, кейсы, квесты
 домашние задания
 дискуссионные вопросы
 риторические вопросы от учеников
 
Иллюстрации
 аудио-, видеоклипы и мультимедиа 
 фотографии, картинки 
 графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты

Дополнения
 рефераты
 статьи 
 фишки для любознательных 
 шпаргалки 
 учебники основные и дополнительные
 словарь терминов                          
 прочие 

Совершенствование учебников и уроков
 исправление ошибок в учебнике
 обновление фрагмента в учебнике 
 элементы новаторства на уроке 
 замена устаревших знаний новыми 
 
Только для учителей
 идеальные уроки 
 календарный план на год  
 методические рекомендации  
 программы
 обсуждения


Интегрированные уроки

Если у вас есть исправления или предложения к данному уроку, напишите нам.

Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.