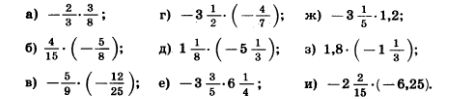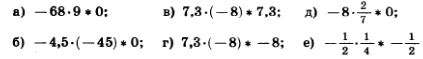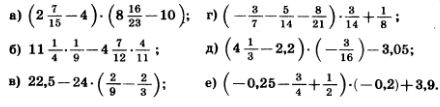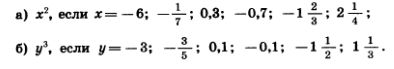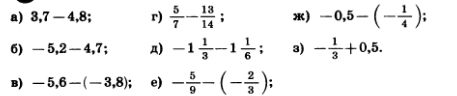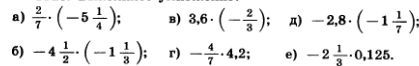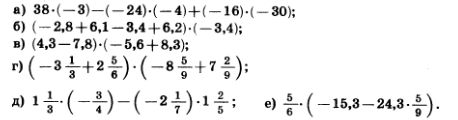|
Гипермаркет знаний>>Математика>>Математика 6 класс>>Математика: Умножение
35. Умножение
Задача 1. Фабрика выпускает в день 200 мужских костюмов. Когда стали выпускать костюмы нового фасона, расход ткани на один костюм изменился на 0,4 м2. На сколько изменился расход ткани на костюмы за день?
Решение. Расход ткани на каждый костюм увеличился на 0,4 м2. Поэтому, чтобы решить задачу, надо умножить 0,4 на 200. Получим 0,4 • 200 = 80. Значит, расход ткани на костюмы за день увеличился на 80 м2, иными словами, изменился на 80 м2
Задача 2. Фабрика выпускает в день 200 мужских костюмов. Когда стали выпускать костюмы нового фасона, расход ткани на один костюм изменился на -0,4 м2. На сколько изменился расход ткани на костюмы за день?
Решение. Расход ткани на каждый костюм уменьшился на 0,4 м2. Поэтому расход ткани на костюмы за день уменьшился на 80 м2 (0,4 •200 = 80). Это значит, что расход ткани на костюмы за день изменился на -80 м2.
Таким образом, произведение -0,4 и 200 равно -80, т. е. -0,4 • 200= - (0,4 • 200) = - 80.
Считают, что и 200 •( —0,4)=—(200 •0,4)=—80.
Чтобы перемножить два числа с разными знаками, надо перемножить модули этих чисел и поставить перед полученным числом знак "—"
Например, (—1,2) •0,3= —(1,2 •0,3)= —0,36;
1,2 •( — 0,3)= -(1,2 •0,3)= -0,36.
Сравнивая эти два произведения с произведением 1,2 •0,3 = 0,36, можно заметить, что при изменении знака любого множителя знак произведения меняется, а его модуль остается тем же.
Если же меняются знаки обоих множителей, то произведение меняет знак дважды и в результате знак произведения не меняется : 8 • 1,1 = 8,8; (- 8) •1,1 = - 8,8; (- 8) • (—1,1)=-(—8,8) = 8,8. Видим, что произведение отрицательных чисел есть число положительное.
Чтобы перемножить два отрицательных числа, надо перемножить их модули.
Например, ( —3,2)•( —9)= | —3,2| • I —9| =3,2•9 = 28,8. Обычно пишут короче: ( — 3,2)•( — 9) = 3,2•9 = 28,8.
Так как (— 3) • 2 = — (3 • 2), то можно первый множитель писать без скобок, т. е. (— 3) • 2 = — 3 • 2.
 Сформулируйте правило умножения двух чисел с разными знаками. Как перемножаются два отрицательных числа? Сформулируйте правило умножения двух чисел с разными знаками. Как перемножаются два отрицательных числа?
 1102. Уровень воды в реке изменяется каждые сутки на а дм. Как изменится уровень воды в реке за 3 суток, если а = 4; —3? 1102. Уровень воды в реке изменяется каждые сутки на а дм. Как изменится уровень воды в реке за 3 суток, если а = 4; —3?
1103. При увеличении температуры воздуха на 1 °С столбик ртути в термометре поднимается на 3 мм. На сколько изменится высота столбика ртути, если температура воздуха изменится: а) на 15 °С; б) на — 12°С?
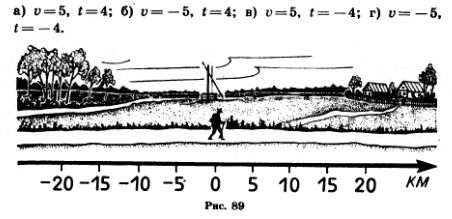
1104. Турист движется по шоссе со скоростью v км/ч. Сейчас он находится в точке 0 (рис. 89). Бели он движется в положительном направлении, то его скорость считают положительной, а в отрицательном направлении — отрицательной. Значение t= —4 означает «4 ч тому назад».
Где будет находиться турист через t ч? Решите задачу при следующих значениях букв:
1105. Выполните умножение:
а) -5•6; ж) 0,7•( — 8); н) 1,2•(-14);
б) 9•( —3); з) -0,5•6; о) -20,5•(-46);
в) — 8•(— 7); и) 12•( —0,2); п) —8,8•302;
г) -10•11; к) -0,6•(-0,9); р) -9,8•(-50,6);
д) 11•( 12); л) -2,5•0,4; с) -17,5•(-17,4);
е) -1,45•0; м) 0•(-1,1); т) 3,08•(-4,05).
1106. Найдите значение выражения — 42y, если у = 0; 1; -1; 3; 5; -30.
 Произведение, в которое входят отрицательные числа, читают так: Произведение, в которое входят отрицательные числа, читают так:
2,4 • (— 0,5) — произведение двух целых четырех десятых и минус нуля целых пяти десятых
— две целых четыре десятых умножить на минус нуль целых пять десятых
-20у — минус двадцать игрек
— произведение минус двадцати и игрек
1107. Найдите значение произведения:
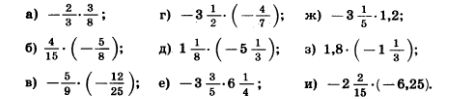
1108. Поставьте вместо * знак < или > так, чтобы получилось верное равенство:
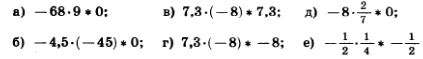
1109. Выполните умножение и сделайте вывод: а) 1 •( —3,9); б) (—1)•7,4; в) —65•( —1); г) -1•7,4.
1110. Запишите в виде произведения сумму:
а) x+x+x+x+x+x в) — 2у — 2у — 2у;
б) —а —а —а —а; г) 5х + 5х + 5х + 5х + 5х.
1111. Найдите значение выражения:
а) х + 4 + x + 4 + х + 4, если х = 9,1;
б) a — 1 +а — 1 + а — 1 + а — 1, если а =—2,1.
1112. Догадайтесь, чему равен корень уравнения, и выполните проверку:
а) —8•x = 72; б) — 4•x=— 40; в) 6•у=—54; г) -6•y = 66.
1113. Найдите значение выражения:
а) 3 • (— 2)+ (— 3) • (— 4) — (— 5) • 7;
б) (-18 + 23-16-1+9)•(-18);
в) ( — 4,5 + 3,8)•(2,01 -3,81);
г) (2,8-3,9)•(-4,3-2,6);
д) — 4,5 • 0,1 + (— 3,7) • (— 2,1) — (— 5,4) • (— 0,2);
е) (2,3• (-1,8) -1,4 • (- 0,8)) • (-1,5);
ж) — 3,8 • (—1,5) — (—1,2) • 0,5 — 6,5;
з) - 2,321 • (- 3,2 + 2,3 - 4,8 + 6,7)-1,579.
1114. Выполните действия:
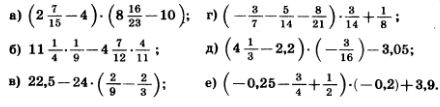
1115. Найдите значение:
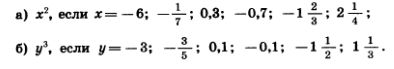
 1116. Выполните действие: 1116. Выполните действие:
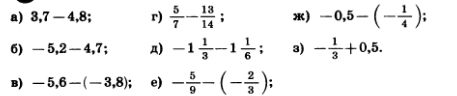
1117. Сравните:
а) |-3,5 + 2,9| и |-3,5| + |2,9|;
б) |-8,7-0,7| и |-8,7| + |-0,7|.
1118. Вычислите устно:
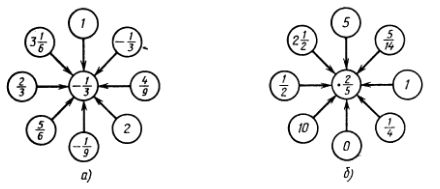
1119. Представьте число —12 в виде разности: а) двух положительных чисел; б) двух отрицательных чисел; в) отрицательного и положительного чисел.
1120. Может ли быть верным равенство а— b = b — а? Приведите примеры. Найдите условие, при котором данное равенство верно.
1121. Может ли разность двух чисел быть больше их суммы?
1122. Подберите такие отрицательные значения х и уу чтобы значение выражения х — у было равно:
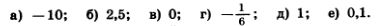
1123. Выполните действия:
а) 3,78-(2,56-2,97); б) -6,19 + (-1,5 + 5,19).
1124. Решите уравнение:
а) х + 3,2 = 1,8; в) 3,7 — х =—2,3;
б) 4,8 — х = 5,6; г) х — 3,9 = — 2,7.
1125. Альбом дороже книги на 1,2 р. Сколько стоит книга и сколько стоит альбом, если известно, что:
а) альбом дороже книги в 1,5 раза;
б) книга в 1,6 раза дешевле альбома;
в) цена книги составляет 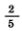 цены альбома; цены альбома;
г) цена книги составляет 0,4 цены альбома;
д) цена книги составляет 80% цены альбома?
1126. Найдите значение выражения:-
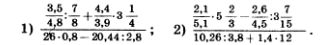
 1127. Найдите значение произведения: 1127. Найдите значение произведения:
а) -24 • 36; д) -4,3 • 5,1; и) -1 • (-1);
б) —48 • ( —15); е) -2,7 • (-6,4); к) (-3)2;
в) 33 • (-11); ж) — 1 • ( — 3,84); л) (-2,5)2;
г) 1,6 • (-2,5); з) -7,2 • 0; м) (-0,2)3.
1128. Выполните умножение:
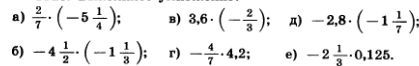
1129. Найдите значение выражения:
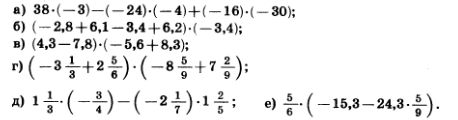
1130. В среду привезли на 4,8 т больше сена, чем во вторник. Сколько тонн сена привезли за эти два дня, если во вторник привезли в 1,4 раза меньше, чем в среду?
1131. Первое число 60. Второе число составляет 80% первого, а третье число составляет 50% суммы первого и второго. Найдите среднее арифметическое этих чисел.
1132. Среднее арифметическое двух чисел равно 12,32. Одно из них составляет треть от другого. Найдите каждое число.
Н.Я.Виленкин, А.С. Чесноков, С.И. Шварцбурд, В.И.Жохов, Математика для 6 класса, Учебник для средней школы
Материалы по математике онлайн, задачи и ответы по классам, планы конспектов уроков по математике скачать
Содержание урока
 конспект урока конспект урока
 опорный каркас опорный каркас
 презентация урока презентация урока
 акселеративные методы акселеративные методы
 интерактивные технологии
Практика интерактивные технологии
Практика
 задачи и упражнения задачи и упражнения
 самопроверка самопроверка
 практикумы, тренинги, кейсы, квесты практикумы, тренинги, кейсы, квесты
 домашние задания домашние задания
 дискуссионные вопросы дискуссионные вопросы
 риторические вопросы от учеников
Иллюстрации риторические вопросы от учеников
Иллюстрации
 аудио-, видеоклипы и мультимедиа аудио-, видеоклипы и мультимедиа
 фотографии, картинки фотографии, картинки
 графики, таблицы, схемы графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты
Дополнения притчи, поговорки, кроссворды, цитаты
Дополнения
 рефераты рефераты
 статьи статьи
 фишки для любознательных фишки для любознательных
 шпаргалки шпаргалки
 учебники основные и дополнительные учебники основные и дополнительные
 словарь терминов словарь терминов
 прочие
Совершенствование учебников и уроков прочие
Совершенствование учебников и уроков
 исправление ошибок в учебнике исправление ошибок в учебнике
 обновление фрагмента в учебнике обновление фрагмента в учебнике
 элементы новаторства на уроке элементы новаторства на уроке
 замена устаревших знаний новыми
Только для учителей замена устаревших знаний новыми
Только для учителей
 идеальные уроки идеальные уроки
 календарный план на год календарный план на год
 методические рекомендации методические рекомендации
 программы программы
 обсуждения
Интегрированные уроки обсуждения
Интегрированные уроки
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.
|