Гипермаркет знаний>>Информатика>>Информатика 11 класс>>Информатика: Прогнозирование по регрессионной модели

                                                              Прогнозирование по регрессионной модели

        Мы получили регрессионную математическую модель и можем прогнозировать процесс путем вычислений. Теперь можно оценить уровень заболеваемости астмой не только для тех значений концентрации угарного газа, которые были получены путем измерений, но и для других значений. Это очень важно с практической точки зрения. Например, если в городе планируется построить завод, который будет выбрасывать в атмосферу угарный газ, то, рассчитав возможную концентрацию газа, можно предсказать, как это отразится на заболеваемости астмой жителей города.

      Существует два способа прогнозов по регрессионной модели. Если прогноз производится в пределах экспериментальных значений независимой переменной (в нашем случае это значение концентрации угарного газа — С), то это называется восстановлением значения.

      Прогнозирование за пределами экспериментальных данных называется экстраполяцией.  Имея регрессионную модель, легко прогнозировать, производя расчеты с помощью электронной таблицы. Выберем для нашего примера в качестве наиболее подходящей квадратичную зависимость. Построим следующую электронную таблицу:


Подставляя в ячейку А2 значение концентрации угарно¬го газа, в ячейке В2 будем получать прогноз заболеваемости. Вот пример восстановления значения:

 

Заметим, что число, получаемое по формуле в ячейке В2, на самом деле является дробным. Однако не имеет смысла считать число людей, даже среднее, в дробных величинах. Дробная часть удалена — в формате вывода числа указано 0 цифр после запятой.
Экстраполяционный прогноз выполняется аналогично.
Табличный процессор дает возможность производить эк¬страполяцию графическим способом, продолжая тренд за пределы экспериментальных данных. Как это выглядит при использовании квадратичного тренда для С = 7, показано на рис. 2.15.
 
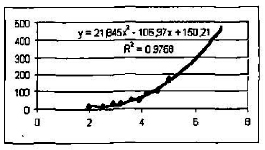
Рис. 2.15. Квадратичный тренд с экстраполяцией
В ряде случаев с экстраполяцией надо быть осторожным. Применимость всякой регрессионной модели ограничена, особенно за пределами экспериментальной области. В на¬шем примере при экстраполяции не следует далеко уходить от величины 5 мг/куб. м. Вполне возможно, что далее ха¬рактер зависимости существенно меняется. Слишком слож¬ной является система «экология — здоровье человека», в ней много различных факторов, которые связаны друг с другом. Полученная регрессионная функция является всего лишь моделью, экспериментально подтвержденной в диапа¬зоне концентраций от 2 до 5 мг/куб. м. Что будет вдали от этой области, мы не знаем* Всякая экстраполяция держится на гипотезе: «предположим, что за пределами эксперимен¬тальной области закономерность сохраняется» - А если не со¬храняется?
Квадратичная модель в данном примере в области малых значений концентрации, близких к 0, вообще не годится. Экстраполируя ее на С = 0 мг/куб. м, получим 150 человек больных» то есть больше, чем при 5 мг/куб. м. Очевидно, это нелепость. В области малых значений С лучше работает экс¬поненциальная модель. Кстати, это довольно типичная ситу¬ация: разным областям данных могут лучше соответство¬вать разные модели.


Коротко о главном


Регрессионная модель может использоваться для прогно¬зирования значений параметров в точках, не являющихся экспериментальными.
Расчет зависимой величины в пределах эксперименталь¬ных значений независимого параметра называется восста¬новлением значения; за пределами — экстраполяцией*
При экстраполяции нельзя далеко уходить от экспери-

может измениться.


Вопросы и задания


1.    $.) Что подразумевается под восстановлением значения no per'
рессионной модели?
б) Что такое экстраполяция?
2.    Соберите данные о средней дневной температуре в вашем городе за последнюю неделю (10 дней, 20 дней). Оцените (хотя бы ш глаз), годится ля использование линейного тренда для описав ния характера изменеяия температуры со временем. Попробуй' те путем графической экстраполяции предсказать температур^ через 2-5 дней.
3.    Придумайте СВОЙ примеры практических задач, для которые имело бы смысл выполнение восстановления значений и экст' раполяционных расчетов.

Семакин И.Г., Хеннер Е.К., Информатика и ИКТ, 11

Отослано читателями из интернет-сайтов

Содержание урока
 конспект урока                       
 опорный каркас  
 презентация урока
 акселеративные методы 
 интерактивные технологии 

Практика
 задачи и упражнения 
 самопроверка
 практикумы, тренинги, кейсы, квесты
 домашние задания
 дискуссионные вопросы
 риторические вопросы от учеников
 
Иллюстрации
 аудио-, видеоклипы и мультимедиа 
 фотографии, картинки 
 графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты

Дополнения
 рефераты
 статьи 
 фишки для любознательных 
 шпаргалки 
 учебники основные и дополнительные
 словарь терминов                          
 прочие 

Совершенствование учебников и уроков
 исправление ошибок в учебнике
 обновление фрагмента в учебнике 
 элементы новаторства на уроке 
 замена устаревших знаний новыми 
 
Только для учителей
 идеальные уроки 
 календарный план на год  
 методические рекомендации  
 программы
 обсуждения


Интегрированные уроки

Если у вас есть исправления или предложения к данному уроку, напишите нам.

Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.