Гипермаркет знаний>>Информатика>>Информатика 11 класс>>Информатика: Использование MS Excel для решения задачи оптимального планирования

                                          Использование MS Excel для решения задачи оптимального планирования

       В математическом программировании существуют свои сложные методы решения задач. Их изучение не входит в наши планы. Поступим так же, как поступали и раньше — воспользуемся тем, что в программу Excel возможности решения задач математического программирования заложены и можно находить решение, не владея его механизмом.

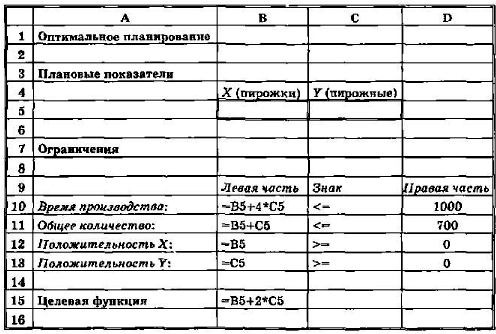
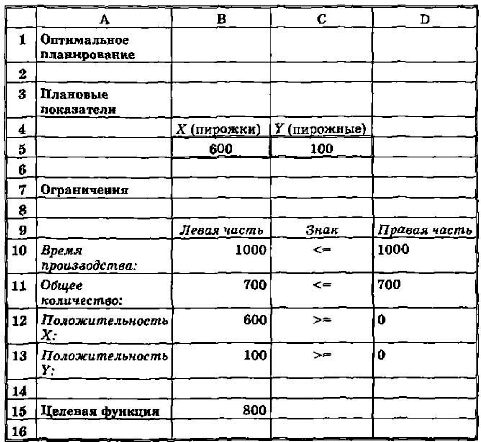
      Средство, о котором идет речь, называется «Поиск решения». Соответствующая команда находится в меню Сервис. «Поиск решения» — одно из самых мощных средств ТП Excel, и мы не будем даже пытаться освоить все его возможности. Покажем на рассмотренном нами простейшем примере («пирожки и пирожные»), как воспользоваться указанным средством.

      Вначале надо подготовить электронную таблицу к решению задачи оптимального планирования. В режиме отображения формул таблица показана на рис. 2.20. Ячейки В5 и С5 зарезервированы соответственно для значений х (план по изготовлению пирожков) и у (план по изготовлению пирожных). Ниже этих ячеек представлена система неравенств , определяющая ограничения на искомые решения. Неравенства разделены на левую часть (столбец В) и правую часть (столбец D). Знаки неравенств в столбце С имеют чисто оформительское значение. Целевая функция' занесена в ячейку В15.
 

           Рис. 2.20. Таблица, подготовленная к вычислению оптимального плана

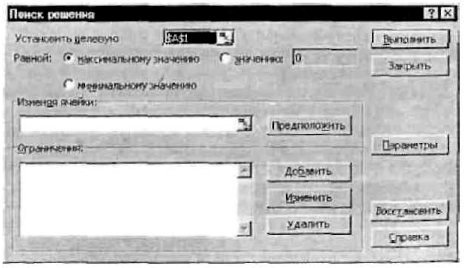
      Теперь следует вызвать программу оптимизации «Поиск решения» и сообщить ей, где расположены данные. Для этого надо выполнить команду => Сервис => Поиск решения. На экране откроется соответствующая форма (рис. 2.21).

             Рис. 2.21. Начальное состояние формы «Поиск решения»

      Далее надо выполнить следующий алгоритм:

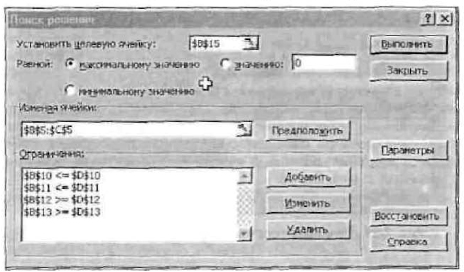
       1. Ввести координату ячейки с целевой функцией. В нашем случае это В15. (Заметим, что если перед этим установить курсор на ячейку В15, то ввод произойдет автоматически).

      2. Поставить отметку «максимальному значению», то есть сообщить программе, что нас интересует нахождение максимума целевой функции.

     3. В поле «Изменяя ячейки» ввести В5:С5, то есть сообщать, какое место отведено под значения переменных  плановых показателей.

     4. В поле «Ограничения» надо ввести информацию о неравенствах-ограничениях, которые имеют вид B10<=D10; B11<=D11; В12>=D12; В13>=D1З. Ограничения вводятся следующим образом:

      => щелкнуть по кнопке «Добавить»;

в появившемся диалоговом окне «Добавление ограничения» ввести ссылку на ячейку В10, выбрать из меню знак неравенства <= и ввести ссылку на ячейку D10; снова щелкнуть по кнопке «добавить» и аналогично ввести второе ограничение B11<=D11 и так далее. В конце надо щелкнуть по кнопке ОК.
Пчмпк р
Восстэкеип,
5.    Закрыть диалоговое окно «Добавление ограничения».
Снова появится форма «Поиск решения» (рис. 2.22).
 



           Рис. 2.22. Форма «Поиск решения» после ввода информации
 
6. Теперь надо дать последние указания: задача является линейной (это многократно облегчит программе ее решение). Для этого следует щелкнуть по кнопке «Параметры»— появится форма «Параметры поиска решения» (рис. 2.23).
 

                             Рис. 2.23. Форма «Параметры поиска решения»

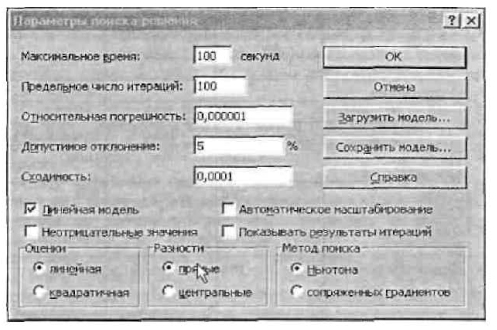
     7. Надо выставить флажок на переключателе «Линейная модель». Остальная информация в форме «Параметры поиска решения» служебная, автоматически устанавливаемые значения нас устраивают, и вникать в их смысл мы не будем. Следует щелкнуть по кнопке ОК, что возвратит нас в форму «Поиск решения».

     8. Вся информация введена. Далее надо щелкнуть по кнопке «Выполнить» — мгновенно в ячейках В5 и С5 появится оптимальное решение (числа 600 и 100), а также число 800 в ячейке В15 — максимальное значение целевой функции (рис. 2.24).
 


                               Рис.2.24. Результаты решения задачи

       Кроме того, на экране появилась еще одна форма — «Результаты поиска решения» (рис. 2.25).

      На первом этапе освоения возможностей программы на эту форму можно не обращать внимания (хотя в принципе в ней может оказаться очень полезная информация).

      Итак, в результате применения инструмента «Поиск решения», мы получим следующий оптимальный план дневного производства кондитерского цеха: нужно выпускать 600 пирожков и 100 пирожных. Эти плановые показатели соответствуют положению точки В на рис. 2.19. В этой точке значение целевой функции f(600,100) = 800. Если один пирожок стоит 2 рубля, то полученная выручка составит 1600 рублей.

      Решение, которое мы получили, вполне разумно как с экономической точки зрения, так и с медицинской. Много сладкого — вредно для здоровья, а пирожки и сытнее, и полезнее.

      Полученная электронная таблица и настроенная на нее сервисная функция «Поиск решения» являются средством, с помощью которого можно решать задачу оптимального планирования при меняющихся условиях. Например, может измениться длина рабочего дня. Тогда надо внести новое значение в ячейку D10, и оптимальный план автоматически пересчитается. Также может измениться допустимое суммарное число изделий в ячейке D11.

      Представьте себе, что в вашей школе учатся неисправимые сладкоежки. И, кроме всех прочих ограничений, перед кондитерским цехом ставится обязательное условие; число пирожных должно быть не меньше числа пирожков. При такой постановке задачи система неравенств  примет вид:

      х + 4у i 1000;

      х + у j 700;

      х j 0

     у j х.

 
       Соответствующее изменение легко внести в электронную таблицу. Для этого достаточно в ячейке D1З вместо 0 записать В5. Результаты поиска решения будут следующими: х = 200, у = 200, f{x,y) = 600. Таким планом вряд ли будет? доволен директор кондитерского цеха, поскольку потери прибыли окажутся очень существенными.

      Следует иметь в виду, что при решении подобных задач могут возникнуть проблемы, о которых мы здесь не говорили. Например, искомого оптимального решения может вовсе не существовать — тогда программа об этом сообщит. Одна ко мы не ставили перед собой цели детально разобраться в задачах оптимального планирования и методах математического программирования. Достаточно того, что вы позкомились с постановкой таких задач и с компьютерными средствами для их решения.

Семакин И.Г., Хеннер Е.К., Информатика и ИКТ, 11

Отослано читателями из интернет-сайтов

Содержание урока
 конспект урока                       
 опорный каркас  
 презентация урока
 акселеративные методы 
 интерактивные технологии 

Практика
 задачи и упражнения 
 самопроверка
 практикумы, тренинги, кейсы, квесты
 домашние задания
 дискуссионные вопросы
 риторические вопросы от учеников
 
Иллюстрации
 аудио-, видеоклипы и мультимедиа 
 фотографии, картинки 
 графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты

Дополнения
 рефераты
 статьи 
 фишки для любознательных 
 шпаргалки 
 учебники основные и дополнительные
 словарь терминов                          
 прочие 

Совершенствование учебников и уроков
 исправление ошибок в учебнике
 обновление фрагмента в учебнике 
 элементы новаторства на уроке 
 замена устаревших знаний новыми 
 
Только для учителей
 идеальные уроки 
 календарный план на год  
 методические рекомендации  
 программы
 обсуждения


Интегрированные уроки

Если у вас есть исправления или предложения к данному уроку, напишите нам.

Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.