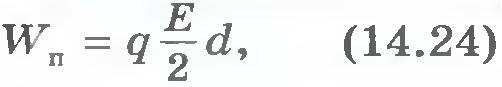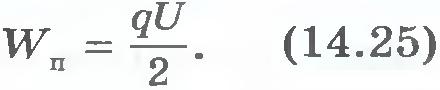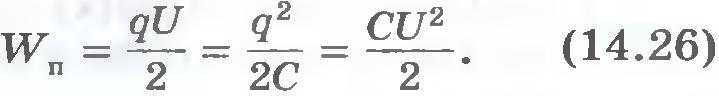Энергия заряженного конденсатора. Применение конденсаторов

KNOWLEDGE HYPERMARKET

Гипермаркет знаний>>Физика и астрономия>>Физика 10 класс>>Физика: Энергия заряженного конденсатора. Применение конденсаторов

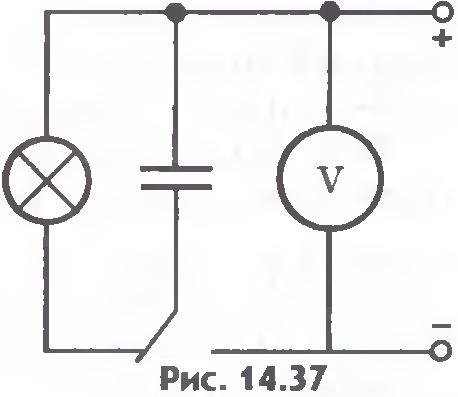
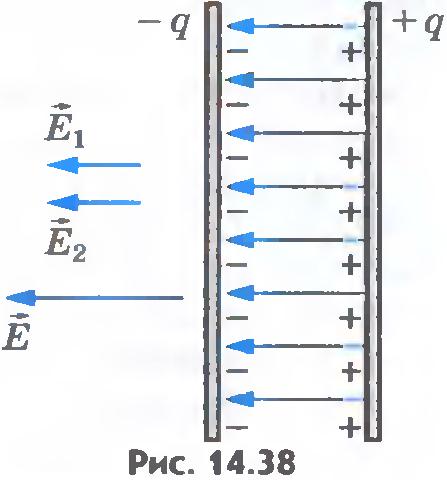
Как и любая система заряженных тел, конденсатор обладает энергией. Вычислить энергию заряженного плоского конденсатора с однородным полем внутри него несложно.
Энергия заряженного конденсатора. Для того чтобы зарядить конденсатор, нужно совершить работу по разделению положительных и отрицательных зарядов. Согласно закону сохранения энергии эта работа равна энергии конденсатора. В том, что заряженный конденсатор обладает энергией, можно убедиться, если разрядить его через цепь, содержащую лампу накаливания, рассчитанную на напряжение в несколько вольт (рис.14.37). При разрядке конденсатора лампа вспыхивает. Энергия конденсатора превращается в тепло и энергию света.

Выведем формулу для энергии плоского конденсатора.
Напряженность поля, созданного зарядом одной из пластин, равна Е/2, где Е -напряженность поля в конденсаторе. В однородном поле одной пластины находится заряд q, распределенный по поверхности другой пластины (рис.14.38). Согласно формуле (14.14) для потенциальной энергии заряда в однородном поле энергия конденсатора равна:

где q - заряд конденсатора, а d - расстояние между пластинами.
Так как Ed=U, где U - разность потенциалов между обкладками конденсатора, то его энергия равна:

Эта энергия равна работе, которую совершит электрическое поле при сближении пластин вплотную.
Заменив в формуле (14.25) разность потенциалов или заряд с помощью выражения (14.22) для электроемкости конденсатора, получим:

   Можно доказать, что эти формулы справедливы для любого конденсатора, а не только для плоского.
   Энергия электрического поля. Согласно теории близкодействия вся энергия взаимодействия заряженных тел сконцентрирована в электрическом поле этих тел. Значит, энергия может быть выражена через основную характеристику поля - напряженность.
   Так как напряженность электрического поля прямо пропорциональна разности потенциалов (U=Ed, то согласно формуле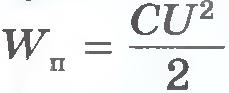

энергия конденсатора прямопропорциональна квадрату напряженности электрического поля внутри него:

.
   Применение конденсаторов. Зависимость электроемкости конденсатора от расстояния между его пластинами используется при создании одного из типов клавиатур компьютера. На тыльной стороне каждой клавиши располагается одна пластина конденсатора, а на плате, расположенной под клавишами, - другая. Нажатие клавиши изменяет емкость конденсатора. Электронная схема, подключенная к этому конденсатору, преобразует сигнал в соответствующий код, передаваемый в компьютер.
   Энергия конденсатора обычно не очень велика - не более сотен джоулей. К тому же она не сохраняется долго из-за неизбежной утечки заряда. Поэтому заряженные конденсаторы не могут заменить, например, аккумуляторы в качестве источников электрической энергии.
   Но это совсем не означает, что конденсаторы как накопители энергии не получили практического применения. Они имеют одно важное свойство: конденсаторы могут накапливать энергию более или менее длительное время, а при разрядке через цепь с малым сопротивлением они отдают энергию почти мгновенно. Именно это свойство широко используют на практике.
   Лампа-вспышка, применяемая в фотографии, питается электрическим током разряда конденсатора, заряжаемого предварительно специальной батареей. Возбуждение квантовых источников света - лазеров осуществляется с помощью газоразрядной трубки, вспышка которой происходит при разрядке батареи конденсаторов большой электроем¬кости.
   Однако основное применение конденсаторы находят в радиотехнике.
   Энергия конденсатора пропорциональна его электроемкости и квадрату напряжения между пластинами. Вся эта энергия сосредоточена в электрическом поле. Энергия поля пропорциональна квадрату напряженности поля.

   ???
   1. Чему равна энергия заряженного конденсатора?
   2. Перечислите основные применения конденсаторов.

Г.Я.Мякишев, Б.Б.Буховцев, Н.Н.Сотский, Физика 10 класс

_{Скачать календарно-тематическое планирование по физике, ответы на тесты, задания и ответы школьнику, книги и учебники, курсы учителю по физике для 10 класса}

Содержание урока
 конспект урока                       
 опорный каркас  
 презентация урока
 акселеративные методы 
 интерактивные технологии 

Практика
 задачи и упражнения 
 самопроверка
 практикумы, тренинги, кейсы, квесты
 домашние задания
 дискуссионные вопросы
 риторические вопросы от учеников
 
Иллюстрации
 аудио-, видеоклипы и мультимедиа 
 фотографии, картинки 
 графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты

Дополнения
 рефераты
 статьи 
 фишки для любознательных 
 шпаргалки 
 учебники основные и дополнительные
 словарь терминов                          
 прочие 

Совершенствование учебников и уроков
 исправление ошибок в учебнике
 обновление фрагмента в учебнике 
 элементы новаторства на уроке 
 замена устаревших знаний новыми 
 
Только для учителей
 идеальные уроки 
 календарный план на год  
 методические рекомендации  
 программы
 обсуждения


Интегрированные уроки

Если у вас есть исправления или предложения к данному уроку, напишите нам.

Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.

Источник — «http://edufuture.biz/index.php?title=%D0%AD%D0%BD%D0%B5%D1%80%D0%B3%D0%B8%D1%8F_%D0%B7%D0%B0%D1%80%D1%8F%D0%B6%D0%B5%D0%BD%D0%BD%D0%BE%D0%B3%D0%BE_%D0%BA%D0%BE%D0%BD%D0%B4%D0%B5%D0%BD%D1%81%D0%B0%D1%82%D0%BE%D1%80%D0%B0._%D0%9F%D1%80%D0%B8%D0%BC%D0%B5%D0%BD%D0%B5%D0%BD%D0%B8%D0%B5_%D0%BA%D0%BE%D0%BD%D0%B4%D0%B5%D0%BD%D1%81%D0%B0%D1%82%D0%BE%D1%80%D0%BE%D0%B2»

При использовании материалов ресурса
ссылка на edufuture.biz обязательна (для интернет ресурсов - гиперссылка).
edufuture.biz 2008-© Все права защищены.
Сайт edufuture.biz является порталом, в котором не предусмотрены темы политики, наркомании, алкоголизма, курения и других "взрослых" тем.

Разработка - Гипермаркет знаний 2008-

Ждем Ваши замечания и предложения на email:
По вопросам рекламы и спонсорства пишите на email: