Гипермаркет знаний>>Геометрия>>Геометрия 7 класс>>Геометрия: Геометрические фигуры. Полные уроки

Геометрические фигуры

Геометрия – это наука о свойствах геометрических фигур. Слово «геометрия» греческое, в переводе на русский язык означает «землемерие». Такое название этой науке было дано потому, что в древнее время главной целью геометрии было измерение расстояний и площадей на земной поверхности.
Геометрия часто применяется на практике. Её надо знать и рабочему, и инженеру, и архитектору, и художнику. Одним словом, геометрию надо знать всем.
Планиметрия – это раздел геометрии, в котором изучаются фигуры на плоскости.
Фигура – это произвольное множество точек на плоскости. Точка, прямая, отрезок, луч, треугольник, круг, квадрат и так далее – всё это примеры геометрических фигур.
Основными геометрическими фигурами на плоскости являются точка и прямая. Этим фигурам в геометрии не даётся определений.
Неопределяемыми геометрическими фигурами на плоскости являются точка и прямая.
Точки принято обозначать прописными латинскими буквами: А, В, С, D …. Прямые обозначаются строчными латинскими буквами: а, b, с, d ….

Фигуры, изучаемые планиметрией:

1. Точка
2. Прямая
3. Параллелограмм (частные случаи: квадрат, прямоугольник, ромб)
4. Трапеция
5. Окружность
6. Треугольник
7. Многоугольник

1) Точка:

В геометрии, топологии и близких разделах математики точкой называют абстрактный объект в пространстве, не имеющий ни объёма, ни площади, ни длины, ни каких-либо других аналогичных характеристик больших размерностей. Таким образом, точкой называют нульмерный объект. Точка является одним из фундаментальных понятий в математике.

Точка в Евклидовой геометри

Точка — это одно из фундаментальных понятий геометрии, поэтому "точка" не имеет определения. Евклид определил точку как то, что нельзя разделить.
Также в геометрии нет определения "прямой" (имеется в виду прямая линия).

2) Прямая:

Прямая — одно из основных понятий геометрии.
Геометрическая прямая (прямая линия) — незамкнутый с двух сторон, протяженный не искривляющийся геометрический объект, поперечное сечение которого стремится к нулю, а продольная проекция на плоскость даёт точку.
При систематическом изложении геометрии прямая линия обычно принимается за одно из исходных понятий, которое лишь косвенным образом определяется аксиомами геометрии.
Если основой построения геометрии служит понятие расстояния между двумя точками пространства, то прямую линию можно определить как линию, путь вдоль которой равен расстоянию между двумя точками.

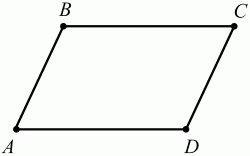
3) Параллелограмм

Параллелограмм— это четырёхугольник, у которого противолежащие стороны попарно параллельны, то есть лежат на параллельных прямых. Частными случаями параллелограмма являются прямоугольник, квадрат и ромб.

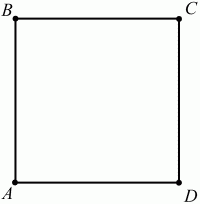
Частные случаи:

Квадрат — правильный четырёхугольник или ромб, у которого все углы прямые, или параллелограмм, у которого все стороны и углы равны.

Квадрат может быть определён как:

• прямоугольник, у которого две смежные стороны равны
• ромб, у которого все углы прямые (любой квадрат является ромбом, но не любой ромб является квадратом).
  

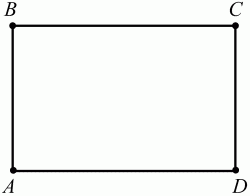
Прямоугольник — это параллелограмм , у которого все углы прямые (равны 90 градусам).
Примечание. В евклидовой геометрии для того, чтобы четырёхугольник был прямоугольником, достаточно, чтобы хотя бы три его угла были прямые. Четвёртый угол (в силу теоремы о сумме углов многоугольника) также будет равен 90°. В неевклидовой геометрии, где сумма углов четырёхугольника не равна 360° - прямоугольников не существует.

Ромб — это параллелограмм, у которого все стороны равны. Ромб с прямыми углами называется квадратом.



4) Трапеция

Трапеция — четырёхугольник, у которого ровно одна пара противолежащих сторон параллельна.
Иногда трапеция определяется как четырёхугольник, у которого пара противолежащих сторон параллельна (про другую не уточняется), в этом случае параллелограмм является частным случаем трапеции. В частности, существует понятие криволинейная трапеция.

Прямоугольная трапеція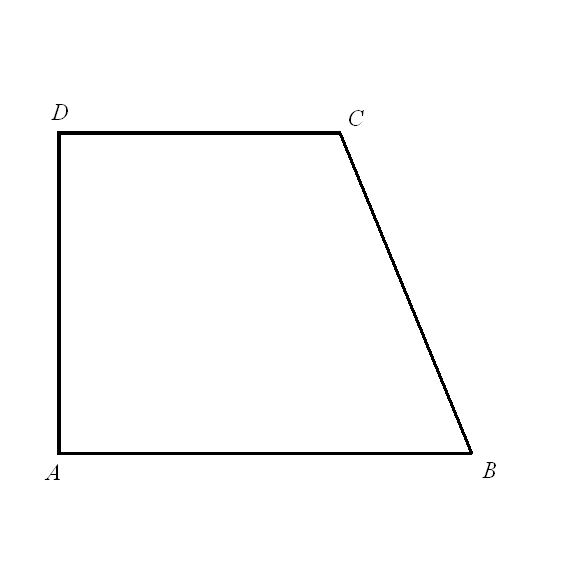
Равнобокая трапеція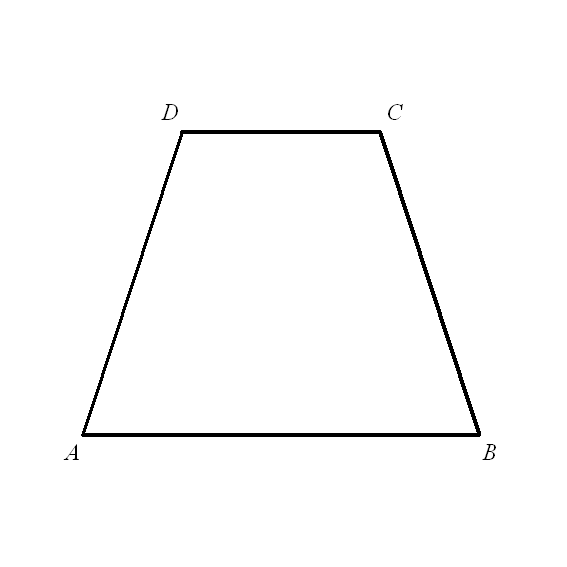

5) Окружность

Окружность — геометрическое место точек плоскости, равноудалённых от заданной точки, называемой центром, на заданное ненулевое расстояние, называемое её радиусом.

6) Треугольник
Треугольник — простейший многоугольник, имеющий 3 вершины (угла) и 3 стороны; часть плоскости, ограниченная тремя точками, и тремя отрезками, попарно соединяющими эти точки.
Если все три точки треугольника лежат на одной прямой, он называется вырожденным.

Файл:19102010 8.gif

7) Многоугольник

Многоугольник — это геометрическая фигура, определяется как замкнутая ломаная. Существуют три различных варианта определения:

• Плоские замкнутые ломаные;
• Плоские замкнутые ломаные без самопересечений;
• Части плоскости, ограниченные ломаными.

Вершины ломаной называются вершинами многоугольника, а отрезки — сторонами многоугольника.

Вопросы:
1) Что изучает геометрия?
2) Как повязаны геометрия и планиметрия?
3) Что такое фигура?
4) Основные фигуры в планиметрии?
5) Рассказать вкратце про каждую из фигур.

Список использованных источников:
1. http://ru.wikipedia.org
2. Павлов А. Н. Геометрия: Планиметрия в тезисах и решениях.
3. Гордин Р. К. Геометрия. Планиметрия. 7-9 классы.

Отредактировано и выслано Потурнаком С. А.

Если у вас есть исправления или предложения к данному уроку, напишите нам.

Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.