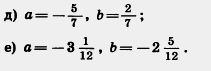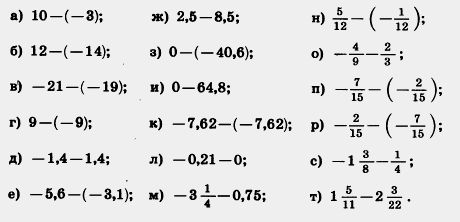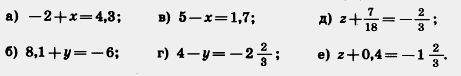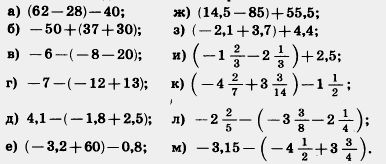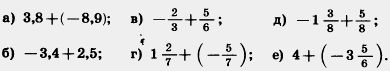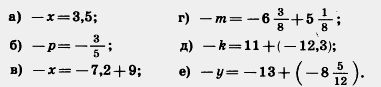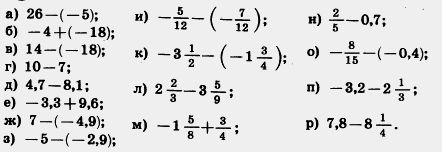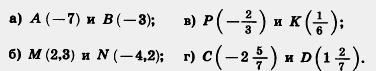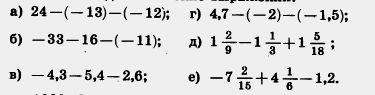Гипермаркет знаний>>Математика>>Математика 6 класс>>Математика: Вычитание-6 класс

34. Вычитание

Вычитание отрицательных чисел имеет тот же смысл, что и вычитание положительных чисел: по заданной сумме и одному из слагаемых находят другое слагаемое. Чтобы найти искомое слагаемое, можно прибавить к сумме число, противоположное известному слагаемому.

Например, 8 + 3 = 11, и потому 11—8 = 3. Но 11 + ( —8) тоже равно 3.

Чтобы из данного числа вычесть другое, надо к уменьшаемому прибавить число, противоположное вычитаемому:

а — b=а + ( — b).

Любое выражение, содержащее лишь знаки сложения и вычитания, можно рассматривать как сумму.

Например, —18 —14= —18 + ( —14); — 8 + 6 — k= — 8 + 6 + (-k).

Разность двух чисел положительна, если уменьшаемое больше вычитаемого, и отрицательна, если уменьшаемое меньше вычитаемого. Если уменьшаемое и вычитаемое равны, то их разность равна нулю.

Задача. Чему равна длина отрезка АВ, если А ( — 5) и В (9)?

Решение. Длина отрезка АВ показывает, на сколько единичных отрезков надо переместить вправо точку А, чтобы она перешла в точку В, т. е. сколько надо прибавить к числу — 5, чтобы получилось число 9. Поэтому если обозначить длину отрезка АВ буквой х, то —5 + x = 9.

Отсюда х = 9 — ( — 5); x = 14.

Значит, длина отрезка равна 14 единичным отрезкам.

Чтобы найти длину отрезка на координатной прямой, надо из координаты его правого конца вычесть координату его левого конца.

?  Что означает вычитание отрицательных чисел?

Каким действием можно заменить вычитание числа а из числа b?

Ответ запишите в виде соответствующего буквенного равенства. Как найти длину отрезка на координатной прямой?

1071. За день температура воздуха изменилась на —12 °С и к вечеру стала равна — 8 °С. Какой была температура утром?

1072.    Температура воздуха утром была 5 °С, а к вечеру она стала равной — 2 °С. На сколько градусов изменилась температура воздуха за день?

1073.    Вчера термометр показывал х °С, сегодня температура понизилась на 12 °С. Какую температуру показывает термометр сегодня, если х=25; 12; 6; 0?

Решите задачу двумя способами: сложением и вычитанием.

1074.    Проверьте равенство а — ( — b)=а+ b, если:

а)    а =18, b = 16;                    г) а= — 4,8, b = 3,9;
б)    а= —2,3, b= —0,5;       
в)    а = 44, b=-7;                     

  Г   Разность, в которую входят отрицательные числа, читают так:

( — 7)—( — 12) — разность минус семи и минус двенадцати
—    из минус семи вычесть минус двенадцать
—    от минус семи отнять минус двенадцать

1075.    Выполните вычитание:

1076.    Решите уравнение и выполните    проверку:

1077.    Представьте в виде суммы разность:

а)    — 28 —( — 32);         в) 50-(-24);               д) -30 —р;
б)    —46 — 30;                г) х —80;                 е) 6 —(—а).

1078.    Назовите каждое слагаемое в сумме:

а)    — 8 + х;                 в) — m — 25;                    д) — n + 9 — k;
б)    z — 6;                    г) 10 — a + y                     е) —а — b — с.

1079.    Составьте сумму из следующих слагаемых:

а)    -x; -у; -4,8;                в) р; -20; 6; -к; 10,3;
б)    1,5; —а; b; — с;        г) —7,6; m; — n; — t; —I.

1080.    Найдите значение выражения:

1081.    Найдите расстояние между точками А (a) и В (b), если:

а)    а = 2, b = 8;                      в) a= — 1, b=6;                    д) а = 3,2, b=— 4,7;
б)    a=—3, b= —5;                   г) а = 5, b=—4;                    е) а=—8,1, b=—2,5.

П  1082. Выполните сложение:

1083.    Найдите значение выражения:
а) 3,75 + ( —2,11)+1,36;                б) -4,27 + (-3,11)+(-0,62).

1084.    Найдите число, противоположное  ;3,85.
1085.    Решите уравнение:

1086.    Между какими соседними целыми числами расположено число:

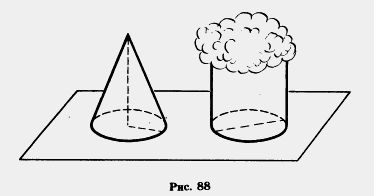
1087.    Запишите все целые числа, модули которых: а) меньше 4; б) больше 4 и меньше 10.

1088.    Может ли сумма двух чисел быть меньше:

а) одного из слагаемых; б) каждого из слагаемых?

Приведите примеры.

М 1089. Высота конуса 24 см, а площадь основания 15 см². Какой высоты должен быть цилиндр с такой же площадью основания, чтобы его объем был равен объему конуса (рис. 88)? Нет ли в задаче лишних данных?

 
1090.    На пришкольном участке было собрано 360 кг овощей. Картофеля было собрано в 5 раз больше, чем свеклы, а капусты — на 80 кг больше, чем свеклы. Сколько килограммов каждой культуры было собрано?

1091.    Решите задачу:
1)    В трех ящиках 21 кг гвоздей. В первом ящике в 1 раза больше гвоздей, чем во втором. Масса гвоздей третьего ящика
составляет массы гвоздей второго ящика. Сколько килограммов гвоздей было в каждом ящике?

2)  В овощеводческом совхозе помидоры, огурцы и морковь занимали 560 га. Посевы моркови составляли площади, занятой под огурцами, а под огурцами занято площади, отведенной под помидоры. Как велика площадь, занятая в отдельности помидорами, огурцами и морковью?

1092.    Выполните действия:

1)    40,1 - 4,06• (29,58:3,48) + 8,112:0,78;
2)    50,2 —3,04• (45,22:4,76)+ 9,202:0,86.

Д 1093. Выполните действие:

1094.    Найдите значение выражения (а+b) — с, если:

а) а = 2,6, b= —1,4, с = 2,1;            б) а=b=—2,4, с=—3,9.

1095.    Отметьте на координатной прямой точки А (— 4) и В (9). Найдите расстояние между точками А и В в единичных отрезках.

1096.    Найдите расстояние в единичных отрезках между точками:

1097.    Найдите значение выражения:

1098.    Заполните пустые места таблицы:

1099. Для учащихся было куплено 70 билетов в кукольный театр. В партер было куплено билетов в 1,5 раза больше, чем на балкон и бельэтаж вместе. Число билетов на балкон составило 0,4 от числа билетов на бельэтаж. Сколько билетов каждого вида было куплено?

1100.    В альбоме 1105 марок, число иностранных марок составило 30% от числа советских марок. Сколько иностранных и сколько советских марок было в альбоме?

1101.    В доме 300 квартир. Однокомнатные квартиры составляют 28% всех квартир дома, а остальные квартиры — двухкомнатные и трехкомнатные, причем двухкомнатных квартир в 1,7 раза больше, чем трехкомнатных. Сколько квартир каждого вида в доме?

   A    Складывать и вычитать отрицательные числа научились древнекитайские ученые еще до нашей эры.

Индийские математики представляли себе положительные числа как «имущества»,а отрицательные числа — как «долги». Вот как индийский математик Брахмагупта (VII в.) излагал правила сложения и вычитания: «Сумма двух имуществ есть имущество», «Сумма двух долгов есть долг», «Сумма имущества и долга равна их разности» и т. д. Попробуйте перевести эти древнеиндийские правила на современный язык.

Н.Я.Виленкин, А.С. Чесноков, С.И. Шварцбурд, В.И.Жохов, Математика для 6 класса, Учебник для средней школы

_{Учебники и книги по всему предметам, домашняя работа, онлайн библиотеки книжек, планы конспектов уроков по математике, рефераты и конспекты уроков по математике для 6 класса скачать}

Содержание урока
 конспект урока
 опорный каркас  
 презентация урока
 акселеративные методы 
 интерактивные технологии 

Практика
 задачи и упражнения 
 самопроверка
 практикумы, тренинги, кейсы, квесты
 домашние задания
 дискуссионные вопросы
 риторические вопросы от учеников

Иллюстрации
 аудио-, видеоклипы и мультимедиа 
 фотографии, картинки 
 графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты

Дополнения
 рефераты
 статьи 
 фишки для любознательных 
 шпаргалки 
 учебники основные и дополнительные
 словарь терминов                          
 прочие 

Совершенствование учебников и уроков
 исправление ошибок в учебнике
 обновление фрагмента в учебнике 
 элементы новаторства на уроке 
 замена устаревших знаний новыми 

Только для учителей
 идеальные уроки 
 календарный план на год  
 методические рекомендации  
 программы
 обсуждения


Интегрированные уроки

Если у вас есть исправления или предложения к данному уроку, напишите нам.

Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.