|
Гипермаркет знаний>>Математика>>Математика 7 класс. Полные уроки>>Геометрия: Геометрические фигуры. Полные уроки
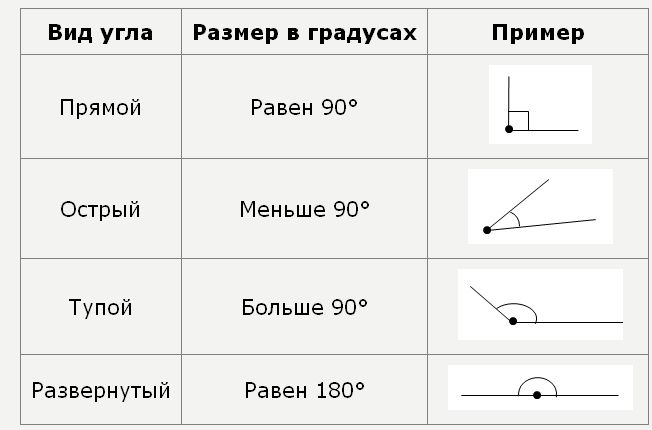
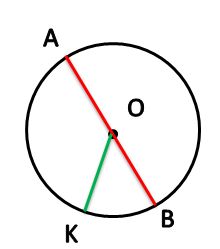
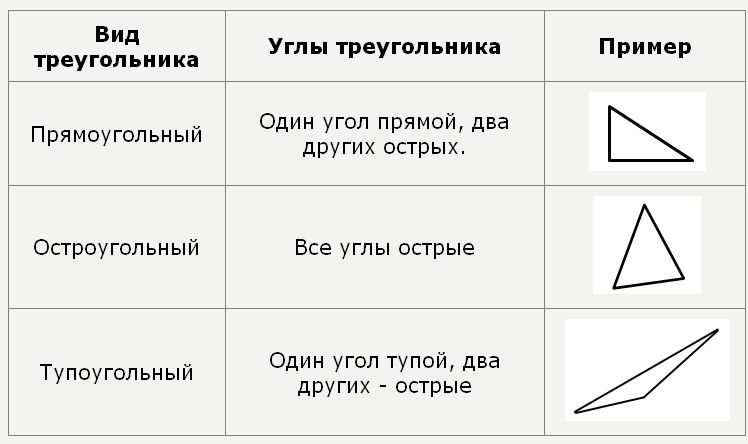
Тема урокаГеометрические фигуры Что такое геометрическая фигураГеометрические фигуры – это совокупность множества точек, линий, поверхностей или тел, которые расположены на поверхности, плоскости или пространстве и формирует конечное количество линий. Термин «фигура» в какой-то степени формально применяется к множеству точек, но как правило фигурой принято называть такие множества, которые расположенные на плоскости и ограничиваются конечным числом линий. Точка и прямая - это основные геометрические фигуры, расположенные на плоскости. К самым простым геометрическим фигурам на плоскости принадлежат - отрезок, луч и ломаная линия. Что такое геометрияГеометрия – это такая математическая наука, которая занимается изучением свойств геометрических фигур. Если дословно перевести на русский язык термин «геометрия», то он обозначает «землемерие», так как в стародавние времена основной задачей геометрии, как науки, стало измерение расстояний и площадей на поверхности земли. Практическое применение геометрии бесценно во все времена и независимо от профессии. Без знаний геометрии не может обойтись ни рабочий, ни инженер, ни архитектор и даже художник. В геометрии есть такой раздел, который занимается изучением различных фигур на плоскости и называется планиметрия. Вам уже известно, что фигурой называют произвольное множество точек, находящиеся на плоскости. К геометрическим фигурам принадлежат: точка, прямая, отрезок, луч, треугольник, квадрат, круг и другие фигуры, которые изучает планиметрия. ТочкаИз выше изученного материала вам уже известно, что точка относится к главным геометрическим фигурам. И хотя это самая малая геометрическая фигура, но она необходима для построения других фигур на плоскости, чертеже или изображении и является основой для всех остальных построений. Ведь построение более сложноватых геометрических фигур складывается из множества точек, характерных для данной фигуры. В геометрии точки обозначают прописными буквами латинского алфавита, например, такими, как: А, В, С, D …. А теперь подведем итог, и так, с математической точки зрения, точка является таким абстрактным объектом в пространстве, который не имеет объема, площади, длины и других характеристик, но остается одним из фундаментальных понятий в математике. Точка – это такой нульмерный объект, которые не имеет определения. По определению Евклида, точкой называют то, что невозможно определить. ПрямаяКак и точка, прямая относится к фигурам на плоскости, которая не имеет определения, так как состоит из бесконечного множества точек, находящихся на одной линии, которая не имеет ни начала ни конца. Можно утверждать, что прямая линия бесконечна и не имеет предела. Если же прямая начинается и заканчивается точкой, то она уже не является прямой и называется отрезком. Но иногда прямая, с одной стороны имеет точку, а с другой нет. В таком случае прямая превращается в луч. Если же взять прямую и на ее средине поставить точку, то она разобьет прямую на два противоположно направленных луча. Данные лучи являются дополнительными. Если же перед вами несколько отрезков, соединенных между собой так, что конец первого отрезка становиться началом второго, а конец второго отрезка — началом третьего и т. д., и эти отрезки находятся не на одной прямой и при соединении имеют общую точку, то такая цепочка является ломаной линией. Задание • Какая ломаная линия называется незамкнутой? Когда конец последнего отрезка ломаной совпадает с началом 1-го отрезка, то такую ломаную линию называют замкнутой. Примером замкнутой ломаной является любой многоугольник. ПлоскостьКак точка и прямая, так и плоскость является первичным понятием, не имеет определения и у нее нельзя увидеть ни начала, ни конца. Поэтому, при рассмотрении плоскости, мы рассматриваем только ту ее часть, которая ограничивается замкнутой ломаной линией. Таким образом, плоскостью можно считать любую гладкую поверхность. Этой поверхностью может быть лист бумаги или стола. УголФигура, которая имеет два луча и вершину, называется углом. Место соединения лучей, является вершиной этого угла, а его сторонами считаются лучи, которые этот угол образуют. Задание: 1. Как в тексте обозначают угол? ПараллелограммПараллелограмм - это четырехугольник, противолежащие стороны которого попарно параллельны. Прямоугольник, квадрат и ромб являются частными случаями параллелограмма. Параллелограмм, имеющий прямые углы равные 90 градусам, является прямоугольником. Квадрат — это тот же параллелограмм, у него и углы и стороны равны. Что до определения ромба, то это такая геометрическая фигура, все стороны которого равны. Кроме того, следует знать, что любой квадрат является ромбом, но не каждый ромб может быть квадратом. ТрапецияПри рассмотрении такой геометрической фигуры, как трапеция, можно сказать, что в частности она, как и четырехугольник имеет одну пару параллельных противолежащих сторон и является криволинейной. Окружность и кругОкружность — геометрическое место точек плоскости, равноудалённых от заданной точки, называемой центром, на заданное ненулевое расстояние, называемое её радиусом. ТреугольникТакже к простым геометрическим фигурам принадлежит и уже изучаемый вами треугольник. Это один из видов многоугольников, у которого часть плоскости ограничена тремя точками и тремя отрезками, которые соединяют эти точки попарно. Любой треугольник имеет три вершины и три стороны. Задание: Какой треугольник называют вырожденным?
МногоугольникК многоугольникам относятся геометрические фигуры разных форм, у которых замкнутая ломаная линия. В многоугольнике все точки, которые соединяют отрезки, являются его вершинами. А отрезки, из которых состоит многоугольник, являются его сторонами.
Интересные факты• А известно ли вам, что возникновение геометрии уходит в глубину веков и связано с развитием различных ремесел, культуры, искусства и наблюдением за окружающим миром. Да и название геометрических фигур является тому подтверждением, так как их термины, возникли не просто так, а благодаря своей схожести и подобию. • Ведь термин «трапеция» в переводе с древнегреческого языка от слова «трапезион» обозначает столик, трапеза и другие производные слова. • «Конус» произошел от греческого слова «конос», что в переводе звучит, как сосновая шишка. • «Линия» имеет латинские корни и происходит от слова «линум», в переводе это звучит, как льняная нить. • А знаете ли вы, что если взять геометрические фигуры с одинаковым периметром, то среди них обладателем самой большой площади оказался круг. • А вот одна из известных картин, созданная еще в начале прошлого века Малевичем, прославляет такую геометрическую фигуру, как квадрат. Черный квадрат на белом фоне является мистической загадкой для окружающих, притягивая к себе исследователей и восхищенные взгляды живописцев. |
Авторські права | Privacy Policy |FAQ | Партнери | Контакти | Кейс-уроки
© Автор системы образования 7W и Гипермаркета Знаний - Владимир Спиваковский
При использовании материалов ресурса
ссылка на edufuture.biz обязательна (для интернет ресурсов -
гиперссылка).
edufuture.biz 2008-© Все права защищены.
Сайт edufuture.biz является порталом, в котором не предусмотрены темы политики, наркомании, алкоголизма, курения и других "взрослых" тем.
Ждем Ваши замечания и предложения на email: 
По вопросам рекламы и спонсорства пишите на email: